文章目录
- 2.6
- 2.7
2.6

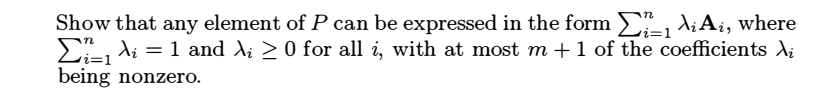
解答:
(a) 设
y
y
y 是
C
C
C 中的一点,多面体
Λ
=
{
(
λ
1
,
…
,
λ
n
)
∈
R
n
∣
∑
i
=
1
n
λ
i
A
i
=
y
,
λ
1
,
…
,
λ
n
≥
0
}
\Lambda=\left\{(\lambda_1, \dots, \lambda_n)\in R^n\mid \sum_{i=1}^n \lambda_i\textbf{A}_i=\textbf{y}, \lambda_1,\dots, \lambda_n\geq 0\right\}
Λ={(λ1,…,λn)∈Rn∣i=1∑nλiAi=y,λ1,…,λn≥0}
是一个标转型多面体,并且是非空的(因为 y y y 是里面的点)。根据课本上推论 2.2,非空标准型多面体必有一个基可行解。根据定理 2.4, 在基解中,非基变量(一共有 n − m n-m n−m 个)的值为零。所以,在 λ 1 , … , λ n \lambda_1,\dots, \lambda_n λ1,…,λn 中,顶多有 m m m 个非零值。
(b) 设
y
y
y 是
P
P
P 中的一点,将
P
P
P 转换成标准型:
P
=
{
[
A
1
′
]
λ
=
[
y
1
]
,
λ
≥
0
}
P=\left\{ \left[ \begin{aligned} \bf A\\ \bf 1' \end{aligned} \right]\mathbf{\lambda} =\left[\begin{aligned} \mathbf{y}\\ 1 \end{aligned} \right], \bf \lambda\geq 0\right\}
P={[A1′]λ=[y1],λ≥0}
由于它是非空标转型多面体,存在一个基可行解。根据定理 2.4,非基变量(一共有 n − m − 1 n-m-1 n−m−1 个)的值为零。所以,在 λ 1 , … , λ n \lambda_1,\dots, \lambda_n λ1,…,λn 中,顶多有 m + 1 m+1 m+1 个非零值。
点评:这道题主要考察了非空标准型多面体必存在一个基可行解到性质(标准型多面体的形式为 { A x = b , x ≥ 0 } \{\bf Ax=b, x\geq 0\} {Ax=b,x≥0})。
- Carathéodory’s theorem 的几何意义是,一个 m m m 维凸包中任意一点都可以由该凸包中顶多 m + 1 m+1 m+1 个点的 凸组合 表示。