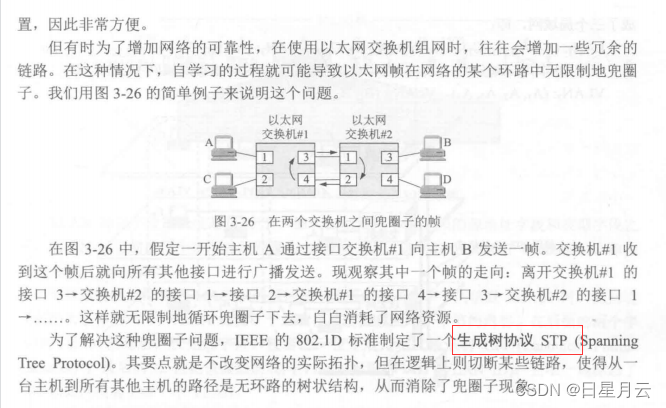
问题引入

为了做到对区间的快速查询,可能你会想到前缀和来优化这个查询,这样区间查询的话是O(1)的复杂度。但如果发生了单点更新,在之后的所有前缀和都要更新,修改的时间复杂度是O(n),并不能解决问题。
线段树

为了避免每次区间查询都要遍历每个元素,我们可以把数字两两求和,并存到另一个数组,这样时间就能节省一半,我们以此类推,就形成了一个 树 的结构
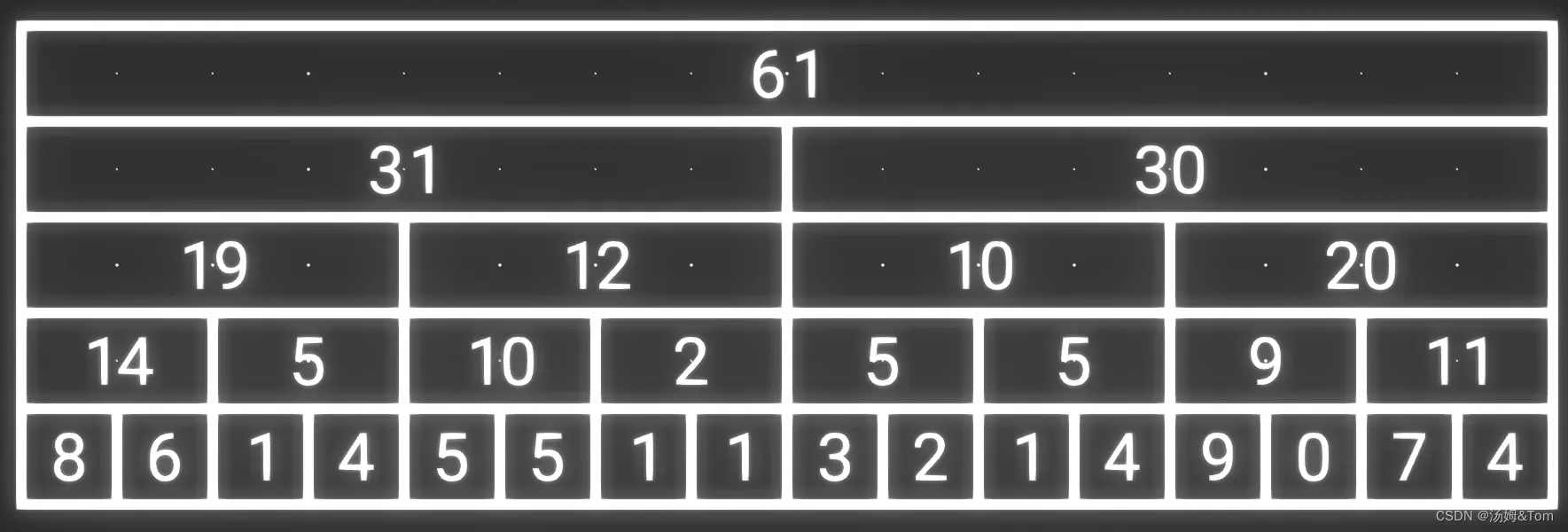
这就是线段树,即便需要求和的数字有很多,我们也可以通过这些额外数组快速求出。
但是同时我们会发现线段树有一些数据是我们不需要的,比如求前2、或者前3个数的和时,我们都用不上 第二层(从下往上)的 第二个元素 5;而在求前4、或者前5个数的和时,我们用第三层(从下往上)的 第一个元素 19更好。
在线段树里类似于这种不需要的数据还有很多,所有层的第偶数个数字都是没用的,去掉也不影响计算
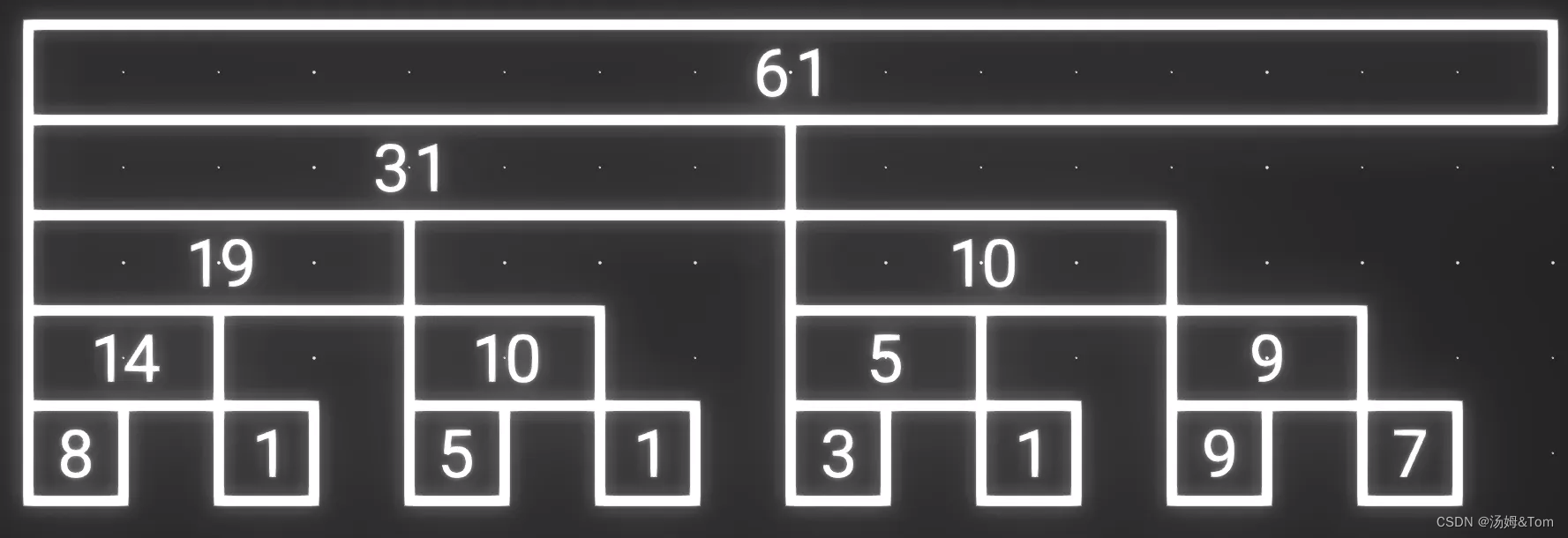
我们观察剩下的数据,会发现刚好有 n 个,我们将其放到一个数组中,这个数组就叫 树状数组
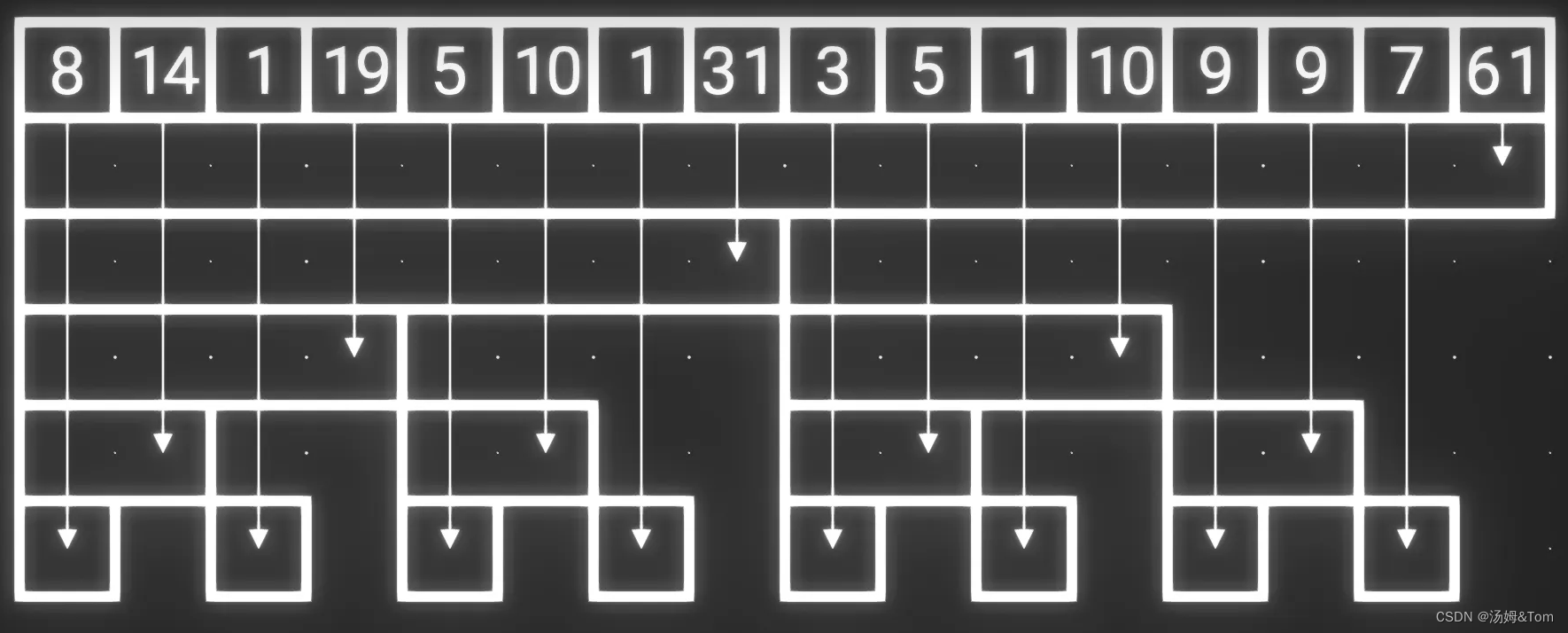
树状数组
树状数组和线段树的区别
线段树比树状数组的扩展性要强,树状数组可以看成是线段树的删减版。线段树能解决的问题,树状数组大部分也可以,但是并不一定都能解决。
树状数组的应用
- 单点修改,区间查询;
- 区间修改,单点查询;
- 区间修改,区间查询
- ......
lowbit函数
如何计算一个非负整数n在二进制下的最低为1及其后面的0构成的数:
例如:44= (101100) (二进制);最低为1和后面的0构成的数是 100 (二进制) = 4
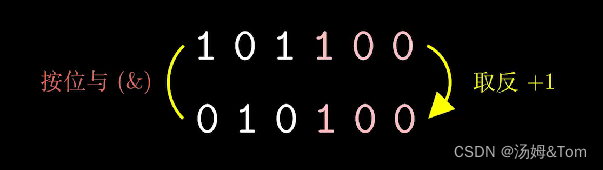
按位与(&)可得到

lowbit(x) = x&(-x)
树状数组结构分析
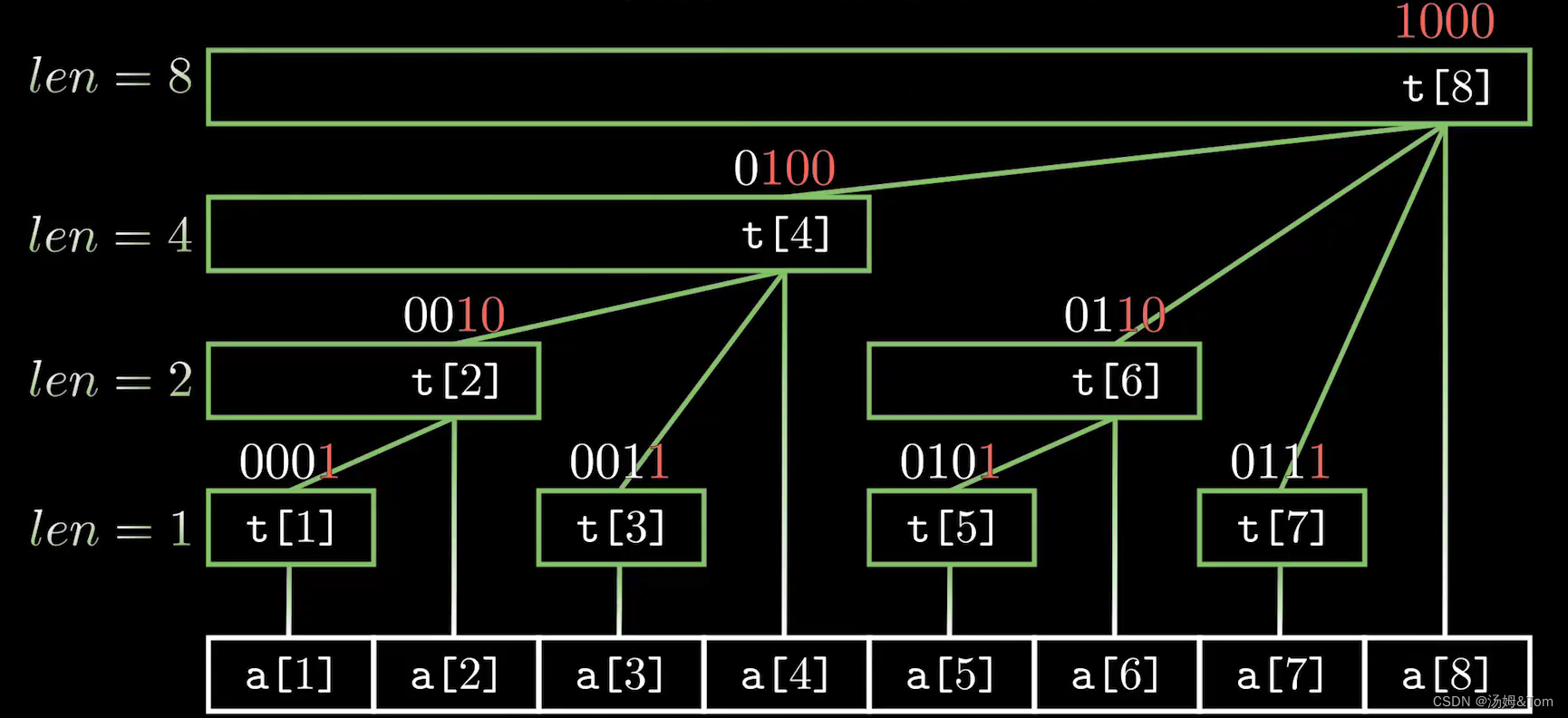
上面是树状数组的结构图,t[x] 保存 以 x 为根的子数中叶子节点值的和,原数组为a[ ]
我们可以发现:
- t[x] 节点覆盖的长度就是 lowbit(x)
- t[x] 节点的父节点为 t[x+ lowbit(x)]
- 整棵树的深度为
单点修改
树状数组从下往上每一层都需要修改
public static void singleAdd(int i,int number){
for(int x=i;x<=n;x+=lowbit(x)){
treeVis[x]+=number;
}
}区间查询
前缀和
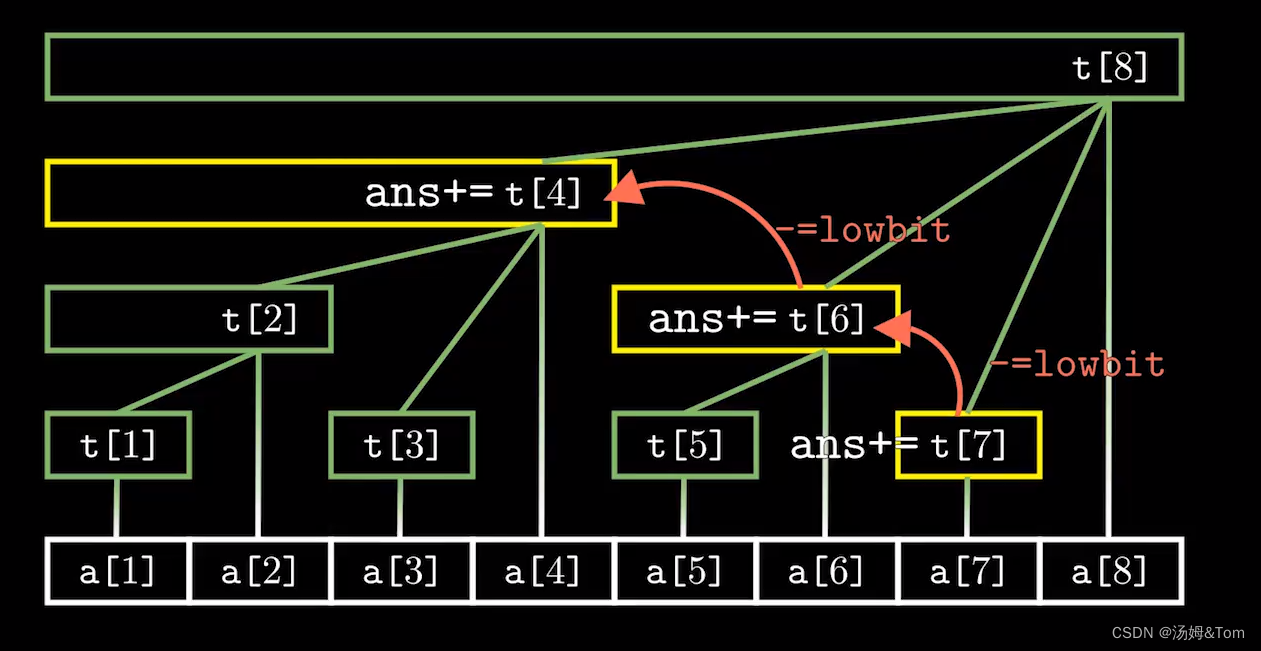
可以发现 向左上找上一个节点 只需要将下标 -= lowbit(这个节点的下标)
这样可根据前缀和求出任意区间和
//求 i 到 j 的区间和
public static int search(int i,int j){
int ans=0;
//求前 j个元素的和
for(int x=j;x>0;x-=lowbit(x))ans+=treeVis[x];
//减去前 i-1个元素的和
for (int x=i-1;x>0;x-=lowbit(x))ans-=treeVis[x];
return ans;
}