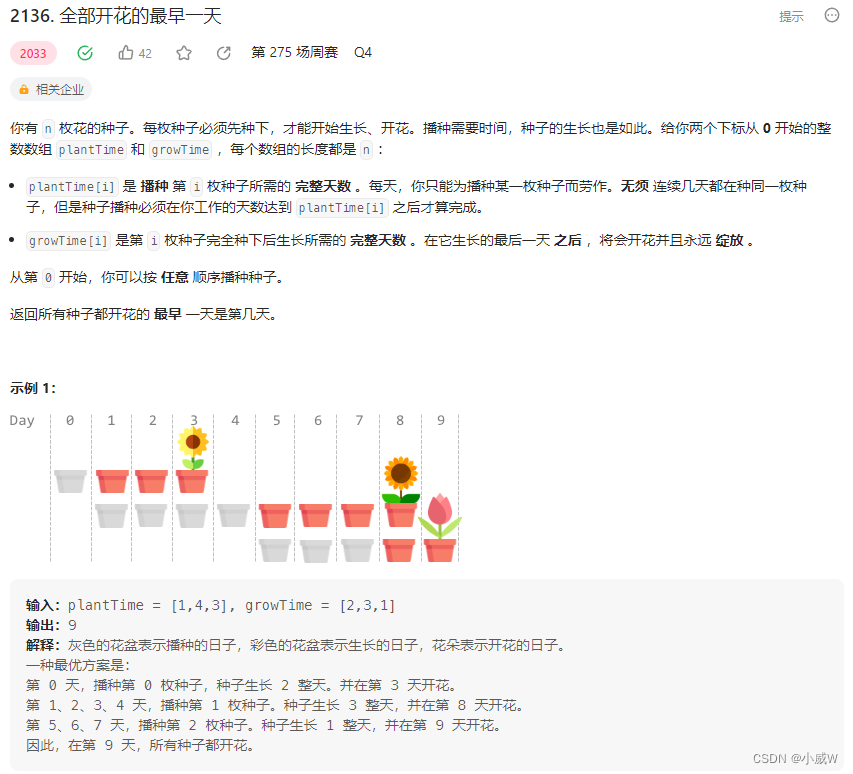
2136. 全部开花的最早一天（贪心）⭐⭐⭐⭐⭐

2136. 全部开花的最早一天
难度：2033

思路

贪心省流版：
花期越长的，越早种植。

完整版：
参见
https://leetcode.cn/problems/earliest-possible-day-of-full-bloom/solutions/1202113/quan-bu-kai-hua-de-zui-zao-yi-tian-by-le-ocxg/
https://leetcode.cn/problems/earliest-possible-day-of-full-bloom/solutions/1200254/tan-xin-ji-qi-zheng-ming-by-endlesscheng-hfwe/

代码

class Solution {
    public int earliestFullBloom(int[] plantTime, int[] growTime) {
        Integer[] id = IntStream.range(0, plantTime.length).boxed().toArray(Integer[]::new);
        Arrays.sort(id, (i, j) -> growTime[j] - growTime[i]);   // 按照开花时间降序排序
        int ans = 0, day = 0;
        for (int i : id) {
            day += plantTime[i];
            ans = Math.max(ans, day + growTime[i]);
        }
        return ans;
    }
}

语法解析：Integer[] id = IntStream.range(0, plantTime.length).boxed().toArray(Integer[]::new);

生成0~plantTime.length - 1的 int 流，然后装箱即转成Integer，最后使用 toArray() 转成数组类型。

注意：这里 toArray() 中必须使用 Integer[]::new，因为这是 Stream 类的 toArray() 方法，
https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/util/stream/Stream.html#toArray(java.util.function.IntFunction)，它返回一个包含此流元素的数组，使用提供的生成器函数来分配返回的数组，以及分区执行或调整大小所需的任何其他数组。

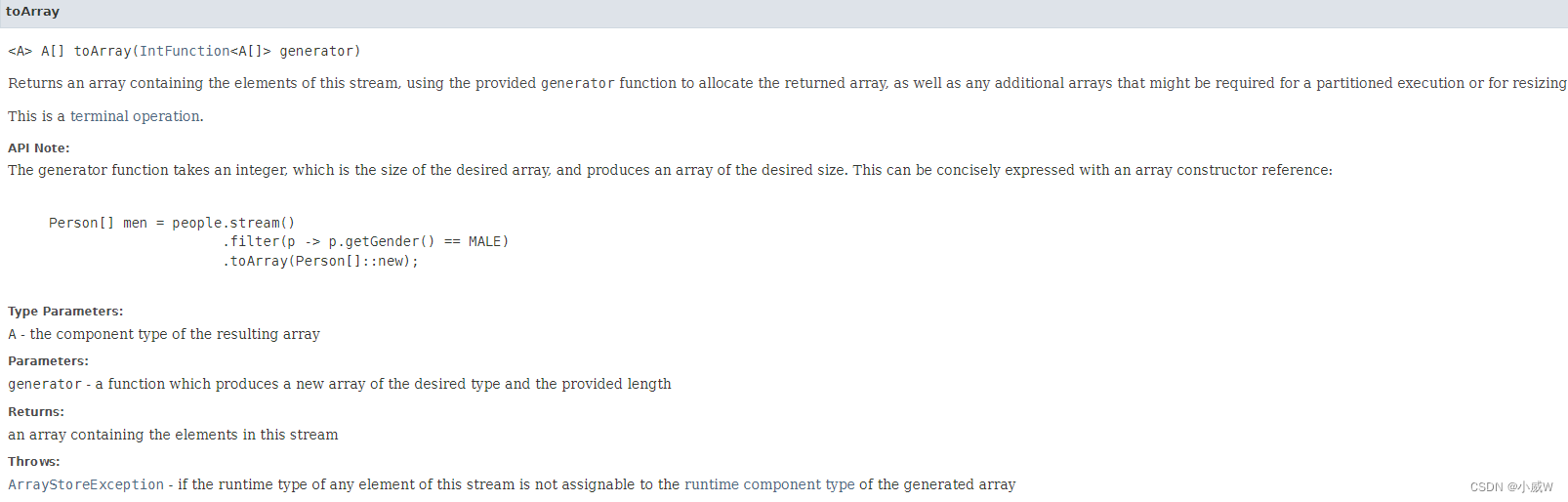
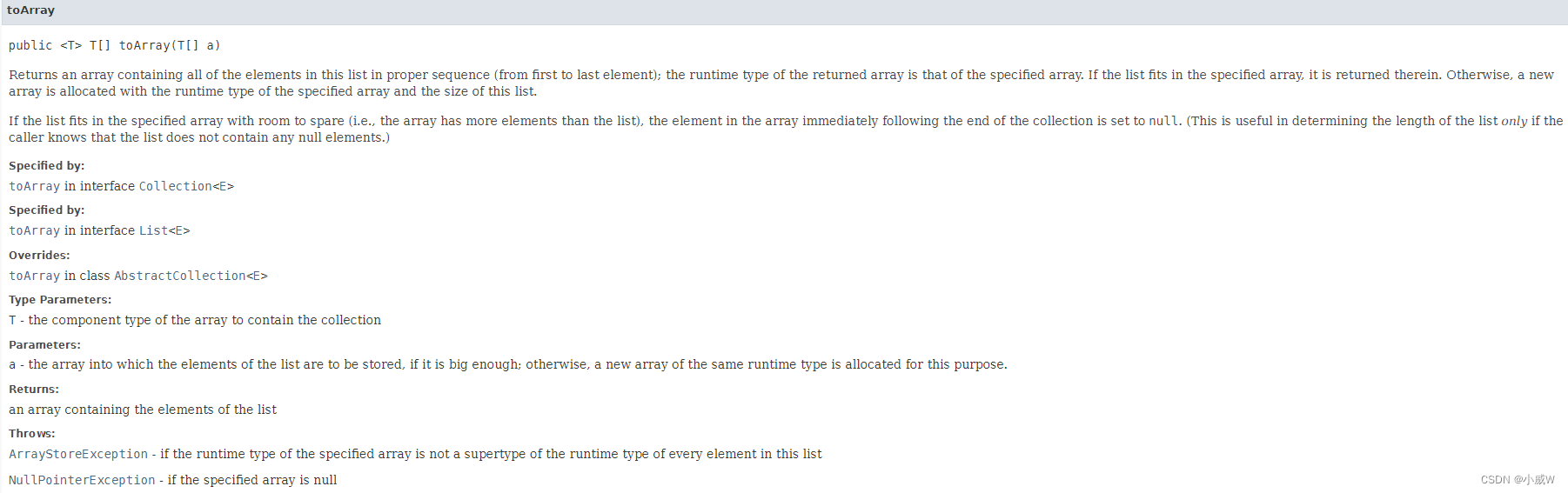
ArrayList 的 toArray 操作如下：
https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/util/ArrayList.html#toArray(T[])

2141. 同时运行 N 台电脑的最长时间（贪心）⭐⭐⭐⭐⭐

2141. 同时运行 N 台电脑的最长时间

难度：2265

提示：

1 <= n <= batteries.length <= 10^5
1 <= batteries[i] <= 10^9

解法1——二分答案

二分是 log ，判断合不合理是 n。
其中判断是否合理的方法基于：电量 > x 的只能被使用 x ，小于 x 的可以充分使用，最后计算这些可用电量之和能否支持 n 个机器运行 x 时长。

class Solution {
    public long maxRunTime(int n, int[] batteries) {
        long l = 0, r = (long)1e15;
        while (l < r) {
            long mid = l + r + 1 >> 1;
            if (op(n, batteries, mid)) l = mid;
            else r = mid - 1;
        }
        return l;
    }

    public boolean op(int n, int[] batteries, long k) {
        long sum = 0;
        for (int battery: batteries) sum += Math.min(battery, k);
        return n <= sum / k;	// 这里不能写成 n * k <= sum; 否则会产生溢出问题
    }
}

解法2——排序+贪心

思路

代码

核心思想就是：先把大的不能充分利用的都给删掉，剩下的小的都可以充分使用所以直接返回 sum / n。

class Solution {
    public long maxRunTime(int n, int[] batteries) {
        long sum = 0;
        for (int battery: batteries) sum += battery;
        Arrays.sort(batteries);
        for (int i = batteries.length - 1; i >= 0; --i) {
            int battery = batteries[i];
            if (battery <= sum / n) {
                return sum / n;     // 剩下的电池都比较小，都可以充分使用
            } else {
                // 消耗掉这个电池
                sum -= battery;
                n--;
            }
        }
        return 0;
    }
}

2234. 花园的最大总美丽值（贪心）

2234. 花园的最大总美丽值
难度：2561

---

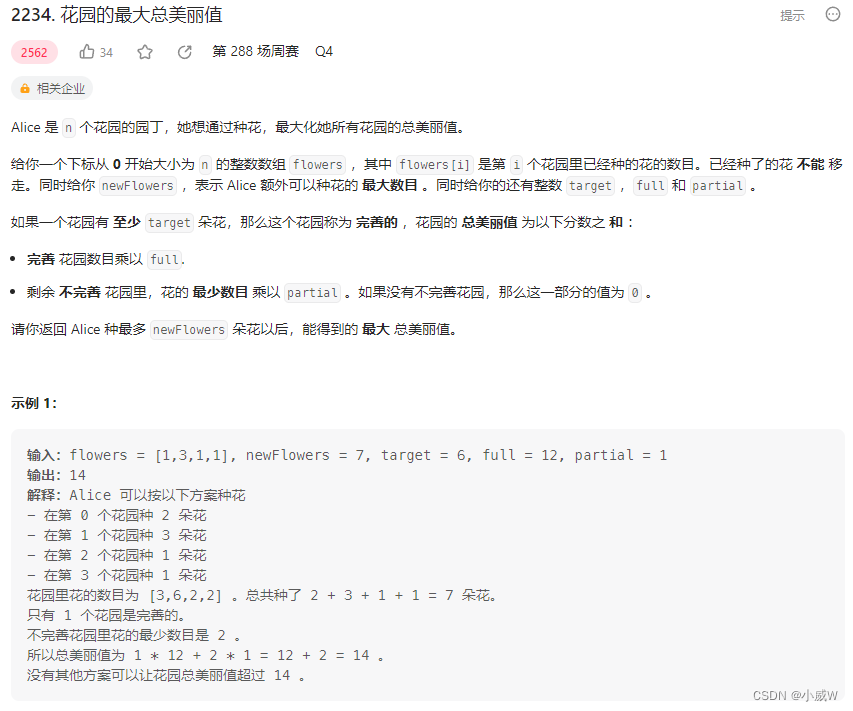
思路是先假设所有花园都可以补到 target ，这时候计算还剩多少个可以用的花朵。

然后从前往后枚举不能补到 target 的前缀，将可以用的花朵逐渐增加，在这个过程中计算不完善花园的最小值最大可以是多少 （leftFlowers + sumFlowers）/ x。

并且在这个枚举过程中不断通过 Math.max() 更新答案。

class Solution {
    public long maximumBeauty(int[] flowers, long newFlowers, int target, int full, int partial) {
        long n = flowers.length;
        Arrays.sort(flowers);  // 升序排序
        if (flowers[0] >= target) return n * full;
        // 填充后缀后剩余可以使用的花朵
        long leftFlowers = newFlowers - target * n; 
        for (int i = 0; i < n; ++i) {
            flowers[i] = Math.min(flowers[i], target);  // 计算多余的花
            leftFlowers += flowers[i];
        }

        long ans = 0L, sumFlowers = 0L;
        for (int i = 0, x = 0; i <= n; ++i) {           // 枚举后缀长度 n - i
            if (leftFlowers >= 0) {                     // 有剩余的花，说明后缀全是full
                // 计算最长前缀的长度。// 剩余的花够补到flowers[x]
                while (x < i && (long)flowers[x] * x - sumFlowers <= leftFlowers) { 
                    // 计算前缀已有花的总数
                    sumFlowers += flowers[x++];         
                }
                long beauty = (n - i) * full;
                // x > 0 说明有前缀，需要确保不会前缀的各个取值不会大于target
                if (x > 0) beauty += Math.min((leftFlowers + sumFlowers) / x, (long)target - 1) * partial;      
                ans = Math.max(ans, beauty);            // 更新答案
            }
            // i不需要补到target，剩余的花数量增加
            if (i < n) leftFlowers += target - flowers[i];  
        }
        return ans;
    }
}

2311. 小于等于 K 的最长二进制子序列（贪心）

2311. 小于等于 K 的最长二进制子序列

难度：1839

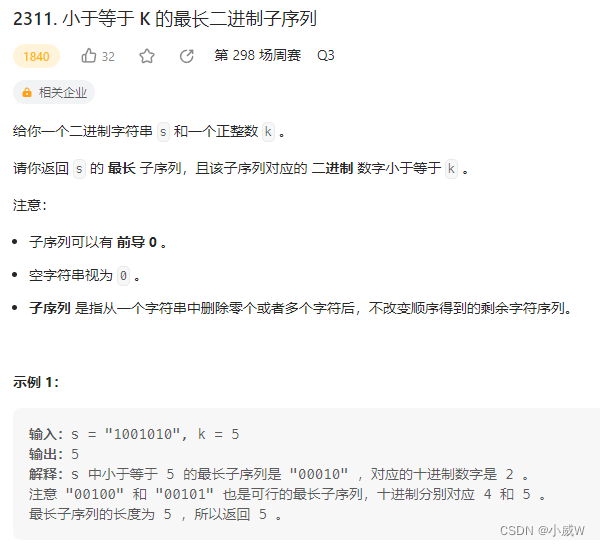
注意是最长子序列 而不是 最长连续子序列。

解法1——双指针删去最前面的1

前导零不会影响二进制数字的大小，当数字过大时，不断删去最开头的1知道数字满足条件即可。

class Solution {
    public int longestSubsequence(String s, int k) {
        int n = s.length(), sum = 0, ans = 0, t = 0;
        List<Integer> nums = new LinkedList();  // 记录1出现的位置
        for (int i = 0; i < n; ++i) {
            ++t;
            sum = sum * 2;
            if (s.charAt(i) == '1') {
                sum++;
                nums.add(i);
            }
            while (sum > k) {                   // 删去最靠前的1
                sum -= 1 << (i - nums.get(0));
                nums.remove(0);
                --t;
            }
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

解法2——分类讨论+贪心

直接看代码中的注释就可以理解思路了。

class Solution {
    public int longestSubsequence(String s, int k) {
        // m是k的2进制中从第一个1到最右边的位数
        int n = s.length(), m = 32 - Integer.numberOfLeadingZeros(k);
        // 如果n<m，那么s全选也会<=k
        if (n < m) return n;
        // 按2进制解析s.substring(n - m)的数值,<=k就可以全选这部分,否则需要删除1位
        var ans = Integer.parseInt(s.substring(n - m), 2) <= k ? m : m - 1;
        // 给结果加上前面的所有0的数量
        return ans + (int) s.substring(0, n - m).chars().filter(c -> c == '0').count();
    }
}

补充：public static int numberOfLeadingZeros​(int i)

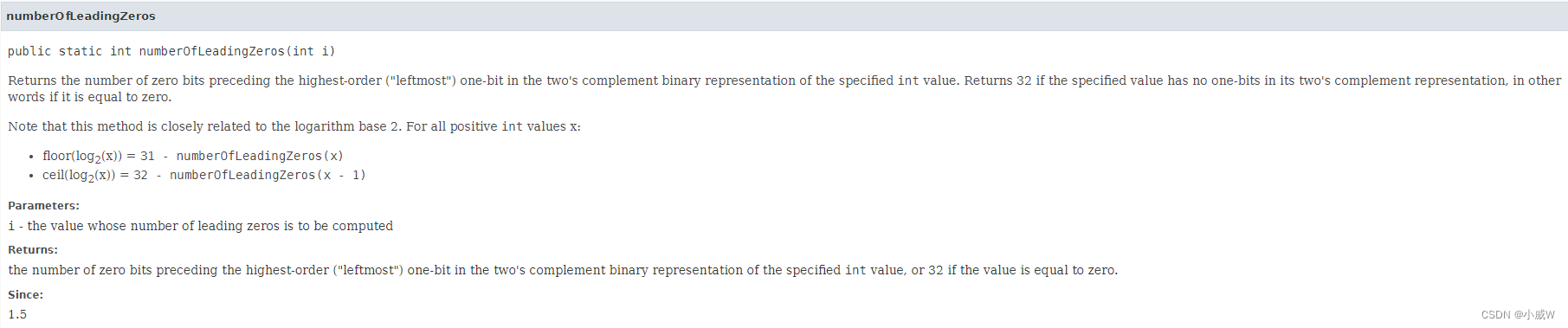
返回指定int值的二进制补码表示中最高阶（“最左边”）一位之前的零位数。如果指定的值在其二进制补码表示中没有一位，即等于零，则返回32。

与之相对的还有：public static int numberOfTrailingZeros​(int i)

返回指定int值的二进制补码表示形式中的最低阶（“最右边”）一位之后的零位数。如果指定的值在其二进制的补码表示中没有一位，即等于零，则返回32。

补充：public static int parseInt​(String s, int radix) throws NumberFormatException

public static int parseInt​(String s, int radix) throws NumberFormatException
https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/lang/Integer.html#parseInt(java.lang.String,int)

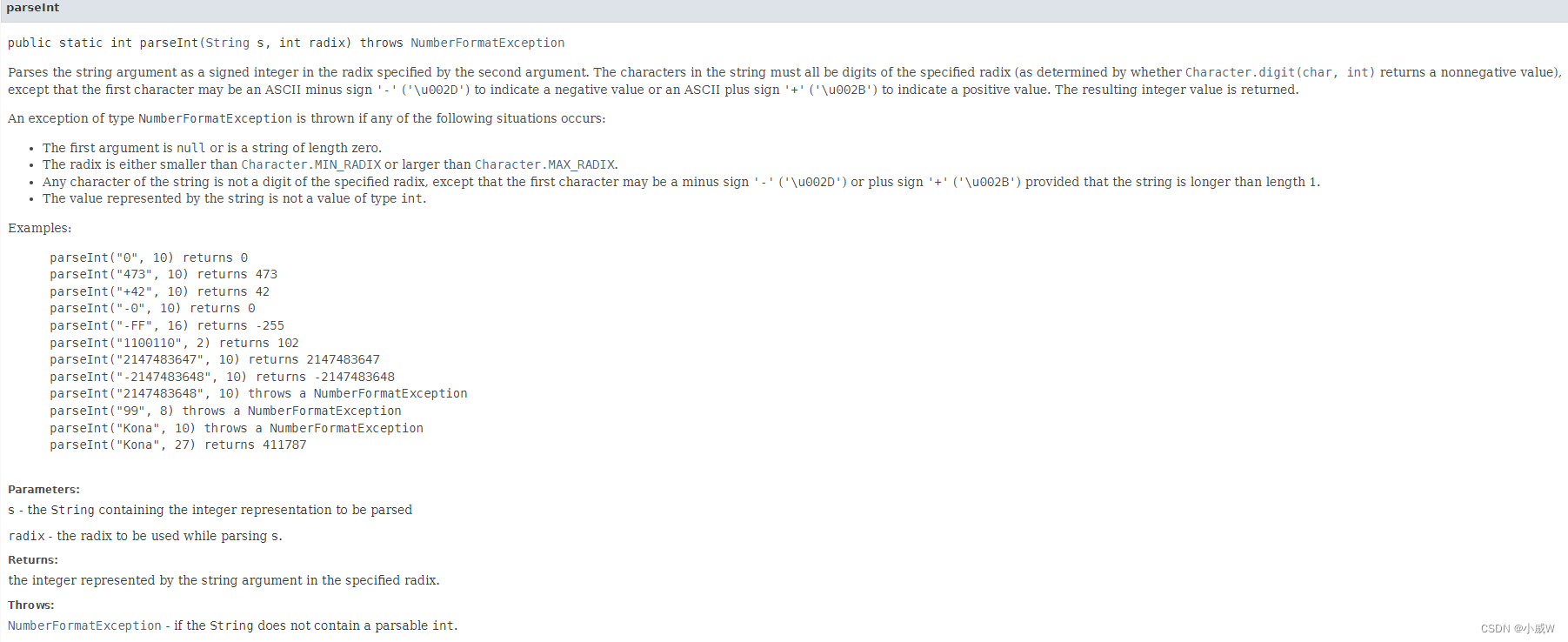
将字符串参数解析为第二个参数指定基数的带符号整数。