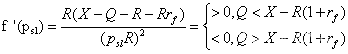论文解读者:陈康明,赵田田,李朋
编者按:
对于大多数一阶算法,我们会在收敛性分析时假设函数是凸的,且梯度满足全局 Lipschitz 条件。而本文中,对于某一类特殊函数。我们不仅不要求函数是凸的,也不再要求梯度满足全局 Lipschitz 条件。
考虑复合优化问题
(
P
)
min
{
Ψ
(
x
)
=
f
(
x
)
+
g
(
x
)
:
x
∈
C
ˉ
}
,
\begin{equation}\nonumber (\mathcal{P})\quad \min \{\Psi(x)=f(x)+g(x): x\in\bar{C}\}, \end{equation}
(P)min{Ψ(x)=f(x)+g(x):x∈Cˉ},
其中
C
ˉ
\bar{C}
Cˉ是
C
C
C的闭包,
C
C
C是
R
d
\mathbb{R}^{d}
Rd的非空开子集。对于大多数一阶算法,我们会在收敛性分析时假设
f
f
f和
g
g
g都是凸函数,且
g
g
g的梯度满足全局 Lipschitz 条件。而本文中,我们不仅不要求函数
f
f
f和
g
g
g是凸函数,也不再要求
g
g
g的梯度的满足全局 Lipschitz 条件,而是使用适应函数g几何形状的凸性条件代替。我们重点研究了一种基于 Bregman 距离而非欧式距离的近端梯度法,该方法涵盖了标准的近端梯度法,并且在一定的合理假设下,证明了该方法全局收敛到临界点。为了展示我们的成果的潜力,我们考虑了一类具有稀疏性约束的二次逆问题,这类问题在许多基础应用中经常出现。并且应用我们的方法推导出了该类问题的新的收敛方案,这是这类重要问题的第一个全局收敛的算法。
第一部分:预备知识
1.1 Bregman 距离
首先我们给出 kernel generating distance 的定义:
定义1.1 (kernel generating distance). 让 C C C是 R d \mathbb{R}^d Rd的凸的非空开集,如果函数 h : R d → ( − ∞ , + ∞ ] h: \mathbb{R}^d \rightarrow(-\infty,+\infty] h:Rd→(−∞,+∞]满足下面的条件,那么它被称为 kernel generating distance :
(i) h h h是适当的,下半连续的凸函数, 并且 dom h ⊂ C ˉ \operatorname{dom} h \subset \bar{C} domh⊂Cˉ, dom ∂ h = C \operatorname{dom} \partial h= C dom∂h=C。
(ii) 在 dom h ≡ C \operatorname{dom} h \equiv C domh≡C上, h h h是 C 1 C^1 C1的。
我们用
G
(
C
)
\mathcal{G}(C)
G(C)表示这类 kernel generating distance。
给定
h
∈
G
(
C
)
h\in\mathcal{G}(C)
h∈G(C),我们可以通过以下方式定义一个近似度量
D
h
:
dom
h
×
int
dom
h
→
R
+
D_h:\operatorname{dom} h\times\operatorname{int} \operatorname{dom} h\rightarrow\mathbb{R}_{+}
Dh:domh×intdomh→R+:
D h ( x , y ) : = h ( x ) − [ h ( y ) + ⟨ ∇ h ( y ) , x − y ⟩ ] D_h(x, y):=h(x)-[h(y)+\langle\nabla h(y), x-y\rangle] Dh(x,y):=h(x)−[h(y)+⟨∇h(y),x−y⟩]
这个近似度量 D h D_h Dh就被称为 Bregman 距离,它衡量了 x x x和 y y y的接近程度。
由于梯度不等式,对于所有的 x ∈ dom h , y ∈ int dom h x\in\operatorname{dom} h, y\in\operatorname{int} \operatorname{dom} h x∈domh,y∈intdomh, h h h是凸的当且仅当 D h ( x , y ) ≥ 0 D_h(x, y)\geq 0 Dh(x,y)≥0。并且如果 h h h是严格凸的,当且仅当 x = y x=y x=y时,等号成立。值得注意的是,一般情况下 D h D_h Dh 不是对称的,除非 h = ∣ ⋅ ∣ 2 h=|\cdot|^2 h=∣⋅∣2,这样得到的就是经典欧式距离的平方。
另外,当 h h h不是凸函数时, D h D_h Dh的结构形式也是有用的。它衡量了在给定点 x ∈ dom h x\in\operatorname{dom} h x∈domh处 h h h的值与其在 y ∈ int dom h y\in\operatorname{int} \operatorname{dom} h y∈intdomh附近的线性近似之间的差异或者说误差。在这种情况下,前面提到的 D h ( x , y ) ≥ 0 D_h(x, y)\geq 0 Dh(x,y)≥0和 D h ( x , y ) = 0 D_h(x, y)= 0 Dh(x,y)=0当且仅当 x = y x=y x=y都不再成立。然而, D h D_h Dh仍然具有两个简单但显著的性质,这些性质可以从基本的代数运算中得出:
三点恒等式:对于任意 y , z ∈ int dom y, z \in \operatorname{int} \operatorname{dom} y,z∈intdom和 x ∈ dom h x \in \operatorname{dom} h x∈domh,我们有 D h ( x , z ) − D h ( x , y ) − D h ( y , z ) = ⟨ ∇ h ( y ) − ∇ h ( z ) , x − y ⟩ D_h(x, z)-D_h(x, y)-D_h(y, z)=\langle\nabla h(y)-\nabla h(z), x-y\rangle Dh(x,z)−Dh(x,y)−Dh(y,z)=⟨∇h(y)−∇h(z),x−y⟩
线性可加性:对于任意 α , β ∈ R \alpha, \beta \in \mathbb{R} α,β∈R,以及任意函数 h 1 h_1 h1和 h 2 h_2 h2,我们有 D α h 1 + β h 2 ( x , y ) = α D h 1 ( x , y ) + β D h 2 ( x , y ) D_{\alpha h_1+\beta h_2}(x, y)=\alpha D_{h_1}(x, y)+\beta D_{h_2}(x, y) Dαh1+βh2(x,y)=αDh1(x,y)+βDh2(x,y)
对于所有 x , y ∈ dom h 1 ∩ dom h 2 x, y \in \operatorname{dom} h_1 \cap \operatorname{dom} h_2 x,y∈domh1∩domh2,使得 h 1 h_1 h1和 h 2 h_2 h2在 y y y处可导。
1.2 L-smooth adaptable 条件我们想要选择合适的函数 h ∈ G ( C ) h\in\mathcal{G}(C) h∈G(C),并用对应的 Bregman 函数 D h D_h Dh来代替近似点梯度法中的欧氏距离平方项。注意,本文所考虑的函数 f f f和 g g g未必是凸函数。其中 g g g满足假设:
g : R d → ( − ∞ , + ∞ ] g:\mathbb{R}^{d}\to (-\infty,+\infty] g:Rd→(−∞,+∞]是适当的下半连续函数,定义域满足$\text{dom}h\subset\text{dom}g , 且 , 且 ,且g 在 在 在C$上连续可微。
基于上述 g g g有关假设, 我们可以给出 L-smooth adaptable 的定义如下:
定义1.2 函数对 ( g , h ) (g,h) (g,h)在 C C C上满足 L-smooth adaptable 条件,当且仅当存在 L > 0 L>0 L>0使得 L h + g Lh+g Lh+g和 L h − g Lh-g Lh−g在 C C C上都是凸函数。
结合1.1节中 Bregman 函数的定义,容易得到它的一个等价定义:
定义1.2’ 函数对 ( g , h ) (g,h) (g,h)在 C C C上满足 L-smooth adaptable 条件,当且仅当存在 L > 0 L>0 L>0使得KaTeX parse error: {equation} can be used only in display mode.
上述定义可看作是 L-smooth 条件的推广。如果取
C
=
R
d
C=\mathbb{R}^{d}
C=Rd,
h
=
1
2
∥
⋅
∥
2
h=\frac{1}{2}\|\cdot\|^{2}
h=21∥⋅∥2, 则对应的不等式可写为
∣
D
g
(
x
,
y
)
∣
=
∣
g
(
x
)
−
g
(
y
)
−
<
∇
g
(
y
)
,
x
−
y
>
∣
≤
L
2
∥
x
−
y
∥
2
,
∀
x
,
y
∈
R
d
,
\begin{equation}\nonumber \left|D_g(x,y)\right|=|g(x)-g(y)-\left<\nabla{g}(y),x-y\right>|\leq \frac{L}{2}\|x-y\|^{2}, \quad \forall x,y\in\mathbb{R}^{d}, \end{equation}
∣Dg(x,y)∣=∣g(x)−g(y)−⟨∇g(y),x−y⟩∣≤2L∥x−y∥2,∀x,y∈Rd,
相当于 g g g满足 L-smooth条件。
另外,第二节的证明只需要 L h − g Lh-g Lh−g是凸函数这个条件。我们把它记作L-smad 条件。
第二部分:BPG 算法
2.1 BPG 算法
根据第一节的分析,我们可以作出以下初步假设:
假设2.1 (1) h ∈ G ( C ) h\in\mathcal{G}(C) h∈G(C), 且 C ‾ = dom h ‾ \overline{C}=\overline{\text{dom}h} C=domh;
(2) f : R d → ( − ∞ , + ∞ ] f:\mathbb{R}^{d}\to (-\infty,+\infty] f:Rd→(−∞,+∞]是适当的下半连续函数,定义域满足 dom f ∩ C ≠ ∅ \text{dom}f\cap{C}\neq\emptyset domf∩C=∅;
(3) g : R d → ( − ∞ , + ∞ ] g:\mathbb{R}^{d}\to (-\infty,+\infty] g:Rd→(−∞,+∞]是适当的下半连续函数,定义域满足 dom h ⊂ dom g \text{dom}h\subset\text{dom}g domh⊂domg,
且 g g g在 C C C上连续可微;(4) ( h , g ) (h,g) (h,g)满足 L-smad 条件;
(5) v ( P ) = inf { Ψ ( x ) : x ∈ C ‾ } > − ∞ v(\mathcal{P})=\inf\{\Psi(x):x\in\overline{C}\}>-\infty v(P)=inf{Ψ(x):x∈C}>−∞.
基于以上假设,我们可以利用函数
h
h
h,构造求解问题
P
\mathcal{P}
P的 BPG 算法如下:

不妨记 T λ ( x ) : = arg min u ∈ R d { f ( u ) + < ∇ g ( x ) , u − x > + 1 λ D h ( u , x ) } T_{\lambda}(x):=\argmin\limits_{u\in\mathbb{R}^d}\left\{f(u)+\left<\nabla{g}(x),u-x\right>+\frac{1}{\lambda}D_h(u,x)\right\} Tλ(x):=u∈Rdargmin{f(u)+⟨∇g(x),u−x⟩+λ1Dh(u,x)}
为了保证算法中的 (3.4) 式能够顺利求解,我们需要添加如下假设:
假设2.2 对任意的 λ > 0 \lambda>0 λ>0,都有 lim ∥ u ∥ → ∞ h ( u ) + λ f ( u ) ∥ u ∥ = + ∞ . \lim\limits_{\|u\|\to\infty}\frac{h(u)+\lambda{f}(u)}{\|u\|}=+\infty. ∥u∥→∞lim∥u∥h(u)+λf(u)=+∞.
假设2.3 对任意的 x ∈ C x\in{C} x∈C,都有 T λ ( x ) ⊂ C T_{\lambda}(x)\sub{C} Tλ(x)⊂C.
这两条假设都是易于实现的 [ 1 ] ^{[1]} [1]. 可以证明,在假设2.1—2.3之下,对任意的 x ∈ intdom h x\in\text{intdom}h x∈intdomh和 x ∈ intdom h x\in\text{intdom}h x∈intdomh, T λ ( x ) T_{\lambda}(x) Tλ(x)是 C C C的非空紧子集。此时,我们认为求解 (3.4) 这一步确实是可行的。
2.2 充分下降性质
在假设2.1—2.3之下,可证明算法具有充分下降性质:
引理2.1 对于任意 x ∈ intdom h x\in\text{intdom}h x∈intdomh, λ > 0 \lambda>0 λ>0以及 x + ∈ T λ ( x ) x^{+}\in{T}_{\lambda}(x) x+∈Tλ(x), 都有不等式 λ Ψ ( x + ) ≤ λ Ψ ( x ) − ( 1 − λ L ) D h ( x + , x ) . \begin{equation}\nonumber \lambda\Psi(x^{+})\leq\lambda\Psi(x)-(1-\lambda{L})D_h(x^{+},x). \end{equation} λΨ(x+)≤λΨ(x)−(1−λL)Dh(x+,x).
由 h h h的凸性可知 D h D_h Dh是非负函数。结合引理2.1,可得如下定理:
定理2.1 如果假设2.1—2.3成立, 0 < λ L < 1 0<\lambda{L}<1 0<λL<1, { x k } \{x^k\} {xk}是 BPG 算法生成的序列,则有以下结论:
(1) 序列 { Ψ ( x k ) } \{\Psi(x^k)\} {Ψ(xk)}单调不增;
(2) ∑ k = 0 + ∞ D h ( x k , x k − 1 ) < ∞ \sum_{k=0}^{+\infty}D_h(x^{k},x^{k-1})<\infty ∑k=0+∞Dh(xk,xk−1)<∞, 因此有 D h ( x k , x k − 1 ) → 0 ( k → ∞ ) D_h(x^{k},x^{k-1})\to0 (k\to\infty) Dh(xk,xk−1)→0(k→∞).
(3) min 1 ≤ k ≤ n D h ( x k , x k − 1 ) ≤ λ n ( Ψ ( x 0 ) − Ψ ∗ 1 − λ L ) \min_{1\leq{k}\leq{n}}D_h(x^k,x^{k-1})\leq\frac{\lambda}{n}(\frac{\Psi(x^{0})-\Psi_{*}}{1-\lambda{L}}) min1≤k≤nDh(xk,xk−1)≤nλ(1−λLΨ(x0)−Ψ∗),其中 Ψ ∗ = v ( P ) > − ∞ \Psi_{*}=v(\mathcal{P})>-\infty Ψ∗=v(P)>−∞.
实际上我们不难看出,如果函数 h h h满足假设2.1—2.3,那么 h + σ 2 ∥ ⋅ ∥ 2 h + \frac{\sigma}{2}\|\cdot\|^{2} h+2σ∥⋅∥2一定也满足假设,其中 σ > 0 \sigma>0 σ>0. 因此不妨设 h h h是强凸函数,对应的强凸系数为 σ \sigma σ. 此时定理2.1中的 (3) 可推出 min 1 ≤ k ≤ n ∥ x k − x k − 1 ∥ 2 ≤ λ n Ψ ( x 0 ) − Ψ ∗ σ ( 1 − λ L ) \min_{1\leq{k}\leq{n}}\|x^k-x^{k-1}\|^{2}\leq\frac{\lambda}{n}\frac{\Psi(x^{0})-\Psi_{*}}{\sigma(1-\lambda{L})} min1≤k≤n∥xk−xk−1∥2≤nλσ(1−λL)Ψ(x0)−Ψ∗.
2.3 收敛速度
为了证明算法的全局收敛性,本节我们设 C = R d C=\mathbb{R}^d C=Rd, 并添加了如下假设:
假设2.4 (1) dom h = R d \text{dom}h=\mathbb{R}^d domh=Rd, 且 h h h在 R d \mathbb{R}^d Rd上是 σ − \sigma- σ−强凸的;
(2) ∇ h \nabla{h} ∇h和 ∇ g \nabla{g} ∇g在 R d \mathbb{R}^d Rd上都是局部 Lipschitz 连续的。
在假设2.1—2.4之下,可证明算法生成的序列 { x k } \{x^k\} {xk}是极小化 Ψ \Psi Ψ的一个类梯度下降序列。其定义如下:
定义1.3 记 F : R d → ( − ∞ , + ∞ ] F:\mathbb{R}^d\to(-\infty,+\infty] F:Rd→(−∞,+∞]是适当的下半连续函数。我们称 { x k } \{x^k\} {xk}是极小化 F F F的一个类梯度下降序列,当且仅当以下三个条件成立:
(1) 存在 ρ 1 > 0 \rho_1>0 ρ1>0, 使得 ρ 1 ∥ x k − x k − 1 ∥ 2 ≤ F ( x k ) − F ( x k − 1 ) \rho_1\|x^k-x^{k-1}\|^2\leq{F}(x ^k)-F(x^{k-1}) ρ1∥xk−xk−1∥2≤F(xk)−F(xk−1)对所有 k k k成立;
(2) 存在 ρ 2 > 0 \rho_2>0 ρ2>0,使得对任意的 k k k都存在 ω k + 1 ∈ ∂ F ( x k + 1 ) \omega^{k+1}\in\partial{F}(x^{k+1}) ωk+1∈∂F(xk+1) ,
满足 ∥ ρ k + 1 ∥ ≤ ρ 2 ∥ x k + 1 − x k ∥ \|\rho_{k+1}\|\leq\rho_2\|x^{k+1}-x^k\| ∥ρk+1∥≤ρ2∥xk+1−xk∥;(3) 对于 { x k } \{x^k\} {xk}的聚点 x ˉ \bar{x} xˉ,
不妨设 lim k → ∞ , k ∈ K x k = x ˉ \lim\limits_{k\to\infty,k\in\mathcal{K}}x^k=\bar{x} k→∞,k∈Klimxk=xˉ.
此时有 lim sup k → ∞ , k ∈ K F ( x k ) ≤ F ( x ˉ ) \limsup_{k\to\infty,k\in\mathcal{K}}F(x^k)\leq{F}(\bar{x}) limsupk→∞,k∈KF(xk)≤F(xˉ).
利用类梯度下降序列的性质,我们可以证明算法的全局收敛性。记 Ψ \Psi Ψ的稳定点集合为 crit Ψ = { x ∈ R d : 0 ∈ ∂ Ψ ( x ) = ∂ f ( x ) + ∇ g ( x ) } , \begin{equation}\nonumber \text{crit}\Psi=\{x\in\mathbb{R}^d:0\in\partial\Psi(x)=\partial{f}(x)+\nabla{g}(x)\}, \end{equation} critΨ={x∈Rd:0∈∂Ψ(x)=∂f(x)+∇g(x)},
序列 { x k } \{x^k\} {xk}所有聚点构成的集合为 ω ( x 0 ) \omega(x^0) ω(x0). 对于满足定义1.3的序列 { x k } \{x^k\} {xk}和对应的函数 F F F, 可证明 ω ( x 0 ) \omega(x^0) ω(x0)是 crit F \text{crit}F critF的非空紧子集,且 F F F在 ω ( x 0 ) \omega(x^0) ω(x0)中每点的取值是相同的。进一步,我们可得到如下结论:
定理2.2 如果假设2.1—2.4成立,且 0 < λ L < 1 0<\lambda{L}<1 0<λL<1, 则有:
(1) { x k } \{x^k\} {xk}任意聚点都是 Ψ \Psi Ψ的稳定点;
(2) 如果 Ψ \Psi Ψ满足 KL 性质,那么 ∑ ∥ x k + 1 − x k ∥ < ∞ \sum\|x^{k+1}-x^{k}\|<\infty ∑∥xk+1−xk∥<∞且 { x k } \{x^k\} {xk}收敛到某一个稳定点。
第三部分:数值算例
3.1 问题模型 (SQIP)
为证明算法的有效性,作者用提出的算法近似求解一个二次方程问题,问题的目标是近似寻找一个
x
∈
R
d
x\in \mathbb{R}^{d}
x∈Rd满足下面的一系列方程
x
T
A
i
x
≈
b
i
,
i
=
1
,
2
,
…
,
m
\begin{equation}\nonumber x^{T}A_{i}x \approx b_{i},~i=1,2,\ldots,m \end{equation}
xTAix≈bi, i=1,2,…,m
其中 A i ∈ R d A_{i}\in \\R^{d} Ai∈Rd是对称矩阵, b i ∈ R b_{i}\in \\R bi∈R是包含噪声的测量值。
通常,研究的系统是欠定的,因此一般利用正则项把原始信号的一些先验信息包含进模型。正则项通常用一个函数
f
f
f表示,这个函数可能是非凸、非光滑、扩展值函数 (为包含约束)。当用最小平方模型来描述测量误差,那么问题能够重新描述为
(QIP)
min
{
Ψ
(
x
)
:
=
1
4
∑
i
=
1
m
(
x
T
A
i
x
−
b
i
)
2
+
θ
f
(
x
)
:
x
∈
R
d
}
\begin{equation}\nonumber \text{(QIP)}~~\min\Big\{\Psi(x):=\frac{1}{4}\sum_{i=1}^{m}(x^{T}A_{i}x-b_{i})^{2}+\theta f(x):~x\in \\R^{d}\Big\} \end{equation}
(QIP) min{Ψ(x):=41i=1∑m(xTAix−bi)2+θf(x): x∈Rd}
其中
θ
>
0
\theta>0
θ>0是一个惩罚参数,主要对数据的真实性和正则项
f
f
f之间进行平衡。
定义非凸函数
g
:
R
d
→
R
g:\\R^{d}\rightarrow \\R
g:Rd→R
g
(
x
)
=
1
4
∑
i
=
1
m
(
x
T
A
i
x
−
b
i
)
2
.
g(x)=\frac{1}{4}\sum_{i=1}^{m}(x^{T}A_{i}x-b_{i})^{2}.
g(x)=41∑i=1m(xTAix−bi)2.
函数
g
g
g$在
R
d
\R^{d}
Rd是连续可微的,但是它的梯度不是全局利普希茨连续的,因此不能够采用经典的近端梯度法求解问题(QIP)。
3.2 算法求解
在这一部分,基本空间是
C
≡
R
d
C\equiv \R^{d}
C≡Rd,非凸函数
g
:
R
d
→
R
g:\R^{d}\rightarrow \R
g:Rd→R被定义为
g
(
x
)
=
1
4
∑
i
=
1
m
(
x
T
A
i
x
−
b
i
)
2
.
g(x)=\frac{1}{4}\sum_{i=1}^{m}(x^{T}A_{i}x-b_{i})^{2}.
g(x)=41i=1∑m(xTAix−bi)2.
对于非凸模型,我们考虑下面两种情况:
(a) 凸 l 1 l_{1} l1范数正则项,即 f : R d → R f:\R^{d}\rightarrow \R f:Rd→R,其中 f ( x ) = ∥ x ∥ 1 f(x)=\|x\|_{1} f(x)=∥x∥1
(b)非凸 l 0 l_{0} l0球约束。 f : R d → R f:\R^{d}\rightarrow \R f:Rd→R,其中 f ( x ) = δ B 0 s ( x ) f(x)=\delta_{\mathbb{B}_{0}^{s}}(x) f(x)=δB0s(x), l 0 l_{0} l0球上的指示函数,正整数 s < d s<d s<d,
B 0 s = { x : ∥ x ∥ 0 ≤ s } , \mathbb{B}_{0}^{s}=\{x: \|x\|_{0}\leq s\}, B0s={x:∥x∥0≤s},
∥ x ∥ 0 \|x\|_{0} ∥x∥0 是 l 0 l_0 l0范数,表示向量 x x x的非零元素个数。
为了把我们的方法应用到问题(a)和(b)中,我们首先需要选择一个合适的函数
h
∈
G
(
R
d
)
h\in\mathcal{G}(\\R^{d})
h∈G(Rd)使得对于
(
g
,
h
)
(g,h)
(g,h),
L-smad
\textbf{L-smad}
L-smad成立。这里,我们采用的
h
:
R
d
→
R
h:\R^{d}\rightarrow \R
h:Rd→R为
h
(
x
)
=
1
4
∥
x
∥
2
4
+
1
2
∥
x
∥
2
2
h(x)=\frac{1}{4}\|x\|_{2}^{4}+\frac{1}{2}\|x\|_{2}^{2}
h(x)=41∥x∥24+21∥x∥22
现在,我们证明 L-smad \textbf{L-smad} L-smad成立,即存在 L > 0 L>0 L>0使得 L h − g Lh-g Lh−g在 R d \R^{d} Rd上为凸。
引理3.1 假设 g g g和 h h h是上面定义的函数,那么对任意 L L L满足 L ≥ ∑ i = 1 m 3 ∥ A i ∥ 2 + ∥ A i ∥ ∣ b i ∣ , L\geq \sum_{i=1}^{m}3\|A_{i}\|^{2}+\|A_{i}\||b_{i}|, L≥i=1∑m3∥Ai∥2+∥Ai∥∣bi∣,
函数 L h − g Lh-g Lh−g在 R d \R^{d} Rd上为凸函数。
为了把 2.2 2.2 2.2节的结果应用到问题(a)和(b)中,我们观察到上面的函数 h h h在 R d \R^{d} Rd上是 1 − 1- 1−强凸,很容易看出假设 2.1 − 2.4 2.1-2.4 2.1−2.4是成立的。另外, g g g是实多项式函数,因此是半代数函数。函数 ∥ x ∥ 0 \|x\|_{0} ∥x∥0和 ∥ x ∥ 1 \|x\|_{1} ∥x∥1也是半代数函数([4] 附录5)。因此,由于半代数函数的和是半代数函数,可得模型(a)和(b)的目标函数 Ψ \Psi Ψ是半代数函数,因此提出的BPG算法能够应用到模型(QIP) (a)和(b),且能够产生一个全局收敛序列收敛到 Ψ \Psi Ψ的临界点。另外,对于模型(a)和(b),全局收敛策略具有一个简明的显式迭代步,接下来会详细进行介绍。
在BPG算法中,我们需要计算Bregman近似梯度映射:
T
λ
(
x
)
=
arg
min
{
f
(
u
)
+
⟨
∇
g
(
x
)
,
u
−
x
⟩
+
1
λ
D
h
(
u
,
x
)
:
u
∈
R
d
}
(
λ
>
0
)
.
T_{\lambda}(x)=\arg\min\Big\{f(u)+\langle\nabla g(x),u-x\rangle+\frac{1}{\lambda}D_{h}(u,x):~u\in \R^{d}\Big\}~~(\lambda >0).
Tλ(x)=argmin{f(u)+⟨∇g(x),u−x⟩+λ1Dh(u,x): u∈Rd} (λ>0).
对于模型 (a)和(b),我们将给出这一迭代步能够产生一个显式的解析解。
在描述之前,我们首先介绍一些简便的符号和一些余下章节将用到的著名算子。令
λ
>
0
\lambda>0
λ>0并固定任意
x
∈
R
d
x\in \R^{d}
x∈Rd 。定义
p
≡
p
λ
(
x
)
=
λ
∇
g
(
x
)
−
∇
h
(
x
)
(为了简便,通常省略
λ
和
x
)
\begin{equation}\tag{3.1} p \equiv p_{\lambda}(x)=\lambda \nabla g(x)-\nabla h(x)~~\text{(为了简便,通常省略}\lambda\text{和}x) \end{equation}
p≡pλ(x)=λ∇g(x)−∇h(x) (为了简便,通常省略λ和x)(3.1)
对于
(
g
,
h
)
(g,h)
(g,h),它们梯度的直接计算结果是
p
λ
(
x
)
p_{\lambda}(x)
pλ(x)。现在,忽略掉表达式
T
λ
T_{\lambda}
Tλ中的常数项,可得
T
λ
(
x
)
=
arg
min
{
λ
f
(
u
)
+
⟨
p
λ
(
x
)
,
u
⟩
+
h
(
u
)
:
u
∈
R
d
}
.
\begin{equation}\tag{3.2} T_{\lambda}(x)=\arg\min\Big\{\lambda f(u)+\langle p_{\lambda}(x),u\rangle+h(u):~u\in \R^{d}\Big\}. \end{equation}
Tλ(x)=argmin{λf(u)+⟨pλ(x),u⟩+h(u): u∈Rd}.(3.2)
接下来,我们介绍两个非常著名的算子,它们会用于计算
T
λ
T_{\lambda}
Tλ。
具有参数
τ
\tau
τ的软阈值算子。对任意
y
∈
R
d
y\in \R^{d}
y∈Rd,
S τ ( y ) = arg min x ∈ R d { τ ∥ x ∥ 1 + 1 2 ∥ x − y ∥ 2 } = max { ∣ y ∣ − τ , 0 } sgn ( y ) , \begin{equation}\tag{3.3} S_{\tau}(y)=\arg\min_{x\in\R^{d}}\Big\{\tau\|x\|_{1}+\frac{1}{2}\|x-y\|^{2}\Big\}=\max\{|y|-\tau,0\}\text{sgn}(y), \end{equation} Sτ(y)=argx∈Rdmin{τ∥x∥1+21∥x−y∥2}=max{∣y∣−τ,0}sgn(y),(3.3)
其中绝对值按照分量进行计算。具有参数
τ
\tau
τ的硬阈值算子。对任意
y
∈
R
d
y\in \R^{d}
y∈Rd,
H
τ
(
y
)
=
arg
min
x
∈
R
d
{
∥
x
−
y
∥
2
:
x
∈
B
0
τ
}
=
{
y
i
,
i
≤
τ
,
0
,
否则,
\begin{equation}\tag{3.4} H_{\tau}(y)=\arg\min_{x\in\R^{d}}\Big\{\|x-y\|^{2}:~x\in\mathbb{B}_{0}^{\tau}\Big\}= \begin{cases} y_{i},~~i\leq \tau,\\ 0,~~\text{否则,} \end{cases} \end{equation}
Hτ(y)=argx∈Rdmin{∥x−y∥2: x∈B0τ}={yi, i≤τ,0, 否则,(3.4)
对于问题(a)和(b),我们分别建立 T λ T_{\lambda} Tλ的显式表达式。
命题3.1 ( l 1 l_{1} l1范数正则化的Bregman近似公式) 令 f = ∥ ⋅ ∥ 1 f=\|\cdot\|_{1} f=∥⋅∥1 且对
x ∈ R d x\in\R^{d} x∈Rd,令
v ( x ) : = S λ θ ( p λ ( x ) ) v(x):=S_{\lambda\theta}(p_{\lambda}(x)) v(x):=Sλθ(pλ(x))。那么 x + = T λ ( x ) x^{+}=T_{\lambda}(x) x+=Tλ(x)为
x + = − t ∗ v ( x ) = t ∗ S λ θ ( ∇ h ( x ) − λ ∇ g ( x ) ) , x^{+}=-t^{*}v(x)=t^{*}S_{\lambda\theta}(\nabla h(x)-\lambda\nabla g(x)), x+=−t∗v(x)=t∗Sλθ(∇h(x)−λ∇g(x)), 是显示公式,其中 t ∗ t^{*} t∗是下面方程的唯一正实根,且具有显式公式形式。
t 3 ∥ v ( x ) ∥ 2 2 + t − 1 = 0 t^{3}\|v(x)\|_{2}^{2}+t-1=0 t3∥v(x)∥22+t−1=0
接下来,我们考虑 l 0 l_{0} l0范数约束的稀疏二次逆问题。首先,我们回顾下下面的结果[5,命题4.3,79页]。
引理3.2 如果 0 ≠ a ∈ R d 0\neq a \in \R^{d} 0=a∈Rd和正整数 s < d s<d s<d,可得 max { ⟨ a , z ⟩ : ∥ z ∥ 2 = 1 , ∥ z ∥ 0 ≤ s } = ∥ H s ( a ) ∥ 2 , \max\{\langle a,z \rangle:~\|z\|_{2}=1,~\|z\|_{0}\leq s\}=\|\mathcal{H}_{s}(a)\|_{2}, max{⟨a,z⟩: ∥z∥2=1, ∥z∥0≤s}=∥Hs(a)∥2,
其中最优解为 z ∗ = H s ( a ) / ∥ H s ( a ) ∥ 2 z^{*}=\mathcal{H}_{s}(a)/\|\mathcal{H}_{s}(a)\|_{2} z∗=Hs(a)/∥Hs(a)∥2。
命题3.2 ( l 0 l_{0} l0范数正则化的Bregman近似公式) 令 f = δ B 0 s f=\delta_{\mathbb{B}_{0}^{s}} f=δB0s, x ∈ R d x\in \R^{d} x∈Rd。那么
x + = T λ ( x ) x^{+}=T_{\lambda}(x) x+=Tλ(x)为
x + = − t ∗ ∥ H s ( p λ ( x ) ) ∥ 2 − 1 H s ( p λ ( x ) ) x^{+}=-\sqrt{t^{*}}\|\mathcal{H}_{s}(p_{\lambda}(x))\|_{2}^{-1}\mathcal{H}_{s}(p_{\lambda}(x)) x+=−t∗∥Hs(pλ(x))∥2−1Hs(pλ(x))
其中 t ∗ ≡ η ∗ \sqrt{t^{*}}\equiv \eta^{*} t∗≡η∗是下面立方方程的唯一非负实根
η 3 + η − ∥ H s ( p λ ( x ) ) ∥ 2 = 0. \begin{equation}\tag{3.5} \eta^{3}+\eta-\|\mathcal{H}_{s}(p_{\lambda}(x))\|_{2}=0. \end{equation} η3+η−∥Hs(pλ(x))∥2=0.(3.5)
参考文献:
[1] Bolte, J., Sabach, S., Teboulle, M., & Vaisbourd, Y. (2018). First order methods beyond convexity and Lipschitz gradient continuity with applications to quadratic inverse problems. SIAM Journal on Optimization, 28(3), 2131-2151.
[2] Bauschke, H. H., Bolte, J., & Teboulle, M. (2017). A descent lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications. Mathematics of Operations Research, 42(2), 330-348.
[3] Geiping, J., & Moeller, M. (2018). Composite optimization by nonconvex majorization-minimization. SIAM Journal on Imaging Sciences, 11(4), 2494-2528.
[4] Bolte, Jérôme, Sabach, S. , & Teboulle, M. (2014). Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Mathematical Programming, 146(1-2), 459-494.
[5] Luss, R. , & Teboulle, M. . (2012). Conditional gradient algorithms for rank-one matrix approximations with a sparsity constraint. Siam Review, 55(1), 65-98.