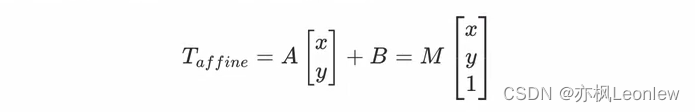图像缩放

        图像缩放是指对图像大小进行调整，对原图进行放大或缩小。图像缩放一般通过插值采样来实现。

        常见的插值方法：最近邻插值、双线性插值、双三次插值。

最近邻插值

        最近邻插值是最简单的一种插值方法，通过映射将原始图片中的像素值映射到放大（或者缩小）后的图片中的每一个位置上即可，而不需要通过计算来得到放大后图片中的每一个像素值。

        其原理很简单，看下面这张图应该就很清晰了。

         最近邻插值计算像素位置的方法如下：

        

                

         : 原图的像素点坐标

        : 缩放后的图中的像素点坐标

        最近邻插值比较简单，但缩放后的图片质量不高。

双线性插值

        双线性插值用原图像中4(2*2)个像素点计算新图像中的1个像素点，效果比双三次插值稍差，但性能比双三次插值要好，属于比较均衡的一种插值方法。

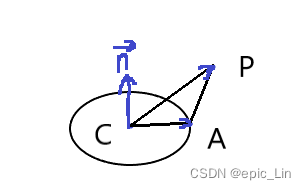
         如上图所示，P点是我们要计算像素值的点，双线性插值首先在水平方向上计算出R1和R2点的值，然后在垂直方向上根据R1,R2计算出P点的值。用数学表达式对应过程如下：

        

        

        

        其中点P坐标为（x,y），Q11坐标为（x1,y1），Q12坐标为（x2,y1），Q21坐标为（x1,y2）,Q22坐标为（x2,,y2）。从公式看计算过程很直白，可以理解为R1,R2的像素值是根据点P在水平方向上相对于左右两个点的水平距离为权计算出来的结果。然后再计算出P在垂直方向上相对于R1,R2两个点垂直距离为权计算出来的结果(距离越近权重越大)。

        综合上面几个式子，可以得出最后P点像素值为：

        

        整理可得：

        

        在数字图像中，实际应用中取的点是四个相邻的点，因此x2 - x1 = 1, y2 - y1 = 1,因此上式的所有分母都是1。在opencv中，双线性插值实际做了一定调整，做了中心对齐：

        

        

        想要详细了解为何这么做，可以参考这里：

双线性插值算法_ABC_Orange的博客-CSDN博客1、线性插值的解释单线性插值法双线性插值法2、另一位牛人讲的比较易懂1.双线性插值2.存在的问题3、又是另一位讲的通俗易懂1，原理2，计算方法3，加速以及优化策略3.1 源图像和目标图像几何中心的对齐　　3.2 将浮点运算转换成整数运算4，代码1、线性插值的解释双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插..._双线性插值https://blog.csdn.net/ABC_ORANGE/article/details/104124928

双三次插值

        双三次（Bicubic）插值又称立方卷积插值，是一种更复杂的插值方法。该算法使用待采样点周围16个点的灰度值作三次插值。三次运算可以得到更接近高分辨率图像的放大效果，但运算量也急剧增加。

        双三次插值的像素值计算公式为：

        从公式可以看出，如果对应代码，上面的式子就相当于二重循环。双三次插值的“双”的意思是对一个4x4大小的像素格子在X和Y两个方向上进行采样。“三次”指的是计算权重的时候，所选用的公式是一个三次多项式。

        双三次插值的权重计算函数为：

                权重函数中：|x|表示的是目标像素点距离某个临近像素点的距离；a是一个经验值，一般取-0.5或-0.75。权重函数的图像大致如下：

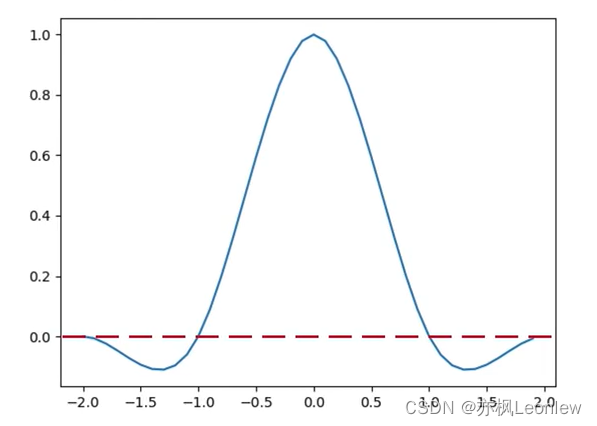
        看下面这幅图：

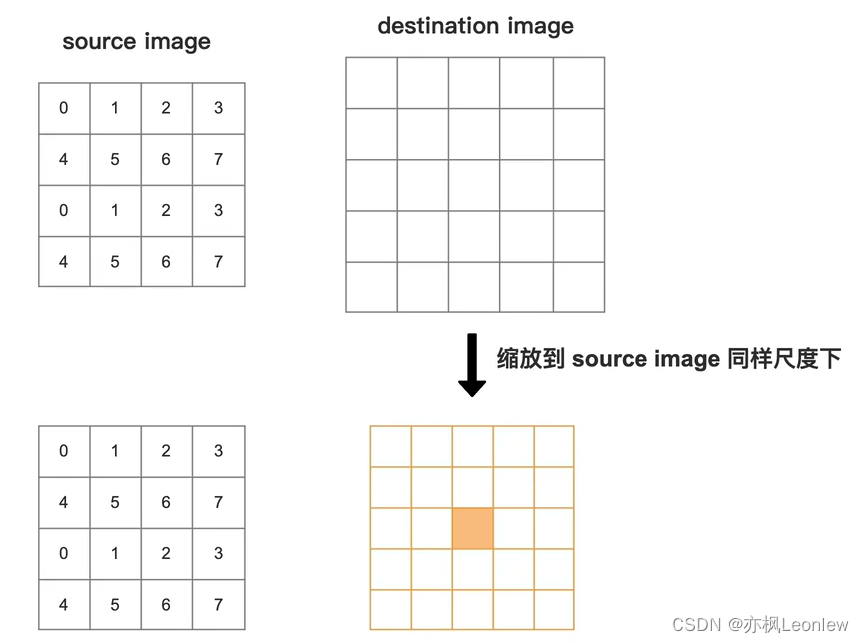
         假设我们要放大原图,source image为原图，destination image为放大后的图。对于目标图中的某个像素点坐标，我们要计算它的像素值，首先就是先找到在原图中它所对应的参考像素点的位置。这里相当于是将目标图缩放到了原图的尺寸下，这样就确定了目标图中像素点计算的时候所对应的原图参考像素点的中心位置。这个步骤和双线性插值是类似的。

        接下来我们以找到的点的位置作为中心点，取出周围16个点的像素值进行插值计算。由于整个计算的重点是对于x和y方向上的权重计算，我们以下面两幅图细化来看权重值的计算：

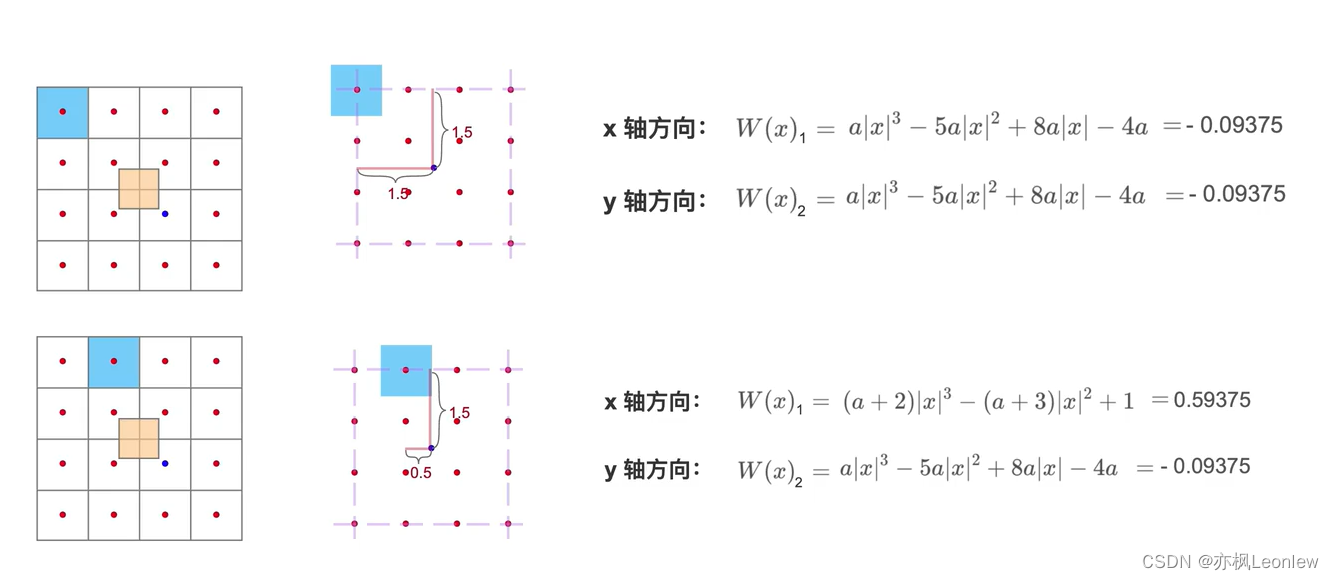
         图中黄色点为中心点，蓝色点是举例用的两个像素点。上下两个图分别展示了两个不同的像素点（蓝色）的权重计算（对中心点像素值的贡献）,其中a = -0.75。

        计算出权重后，我们就可以计算中心点的像素值了,参考下图：

        参考：

        插值算法 ｜ 双三次插值算法_哔哩哔哩_bilibili

图像平移

        图像的平移原理很简单，计算公式如下：

        

        x'和y'是移动后的点的位置，是移动的偏移量。在实际应用中，通常用一个矩阵来表示这种变换，通过矩阵和向量相乘得到目标位置向量（齐次坐标），矩阵为：

        在OpenCV中，平移的API所需要的平移矩阵参数是一个2*3的矩阵：

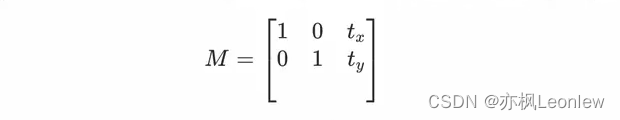
图像旋转

        图像旋转操作是通过一个旋转矩阵变换实现的。旋转矩阵定义（齐次坐标形式）为：

         对于这个矩阵的推导，网上有很多版本，在这里我也来尝试用极坐标推导一下（任意点P，非齐次坐标）。

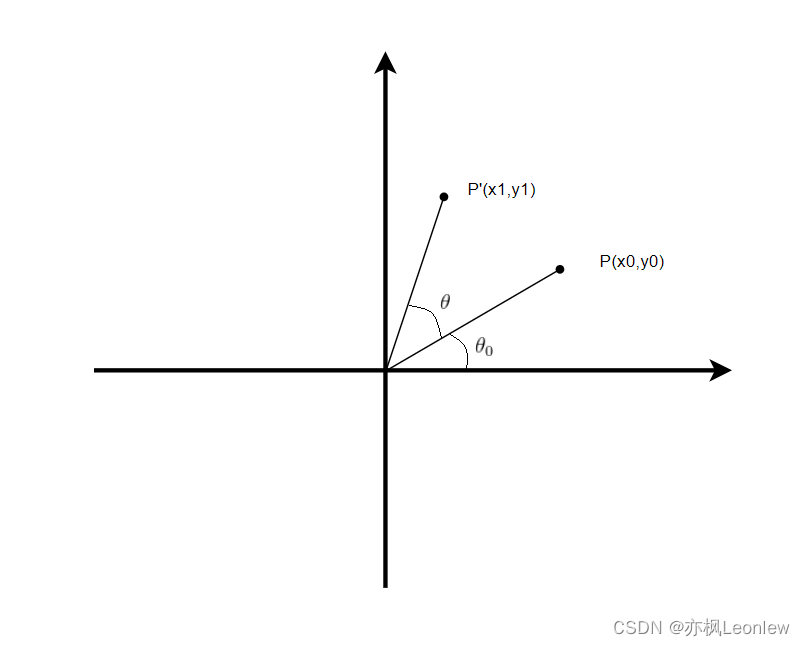
         如上图，图中点P是没有旋转前的位置，P'是P点旋转角度后的位置。P点的坐标(x0,y0)写成极坐标的形式为：

         

        旋转后的点P'极坐标为：

        

        用三角函数的和角公式展开可得:

        

        

        这两个式子其实可以看做是两个变量的线性方程组：

        

        

        这两个线性方程组，写成矩阵方程的形式就是：

        

        由此我们可以得到2x2的旋转矩阵就是

        

图像仿射变换

        图像仿射变换涉及图像的形状、位置、角度的变化，可以理解为图像缩放、旋转、翻转和平移等操作的组合。

        以下图为例：

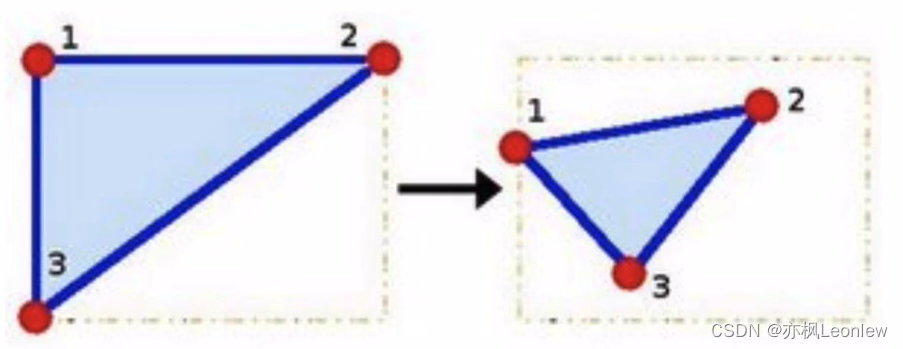
         左图中的点1,2,3和右图中的点是一一对应的，经过映射后的点仍然构成三角形，但三角形的形状发生了较大的改变。这个映射就对应了仿射变换。

        OpenCV中，仿射变换是一个2*3的矩阵：

         

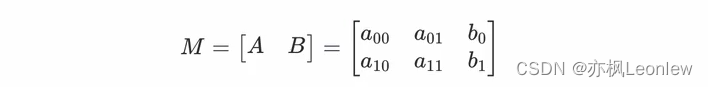
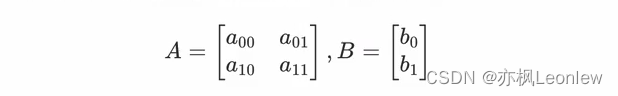
        A是线性变换矩阵，B是平移矩阵。对于任意一个点(x,y)，仿射变换的计算方式为：