官方代码地址:https://github.com/NVlabs/noise2noise
论文地址:https://arxiv.org/abs/1803.04189
第一次接触这方向,相当于翻译了。
摘要
作者通过机器学习将基础统计推理应用于信号重建上:学习将损坏的观察结果(corrupted observations)映射到干净信号上。作者从这个管道得到了一个简单且有力的结论:通过仅查看损坏样例来学习恢复图像,能达到甚至有时会超越那些没有精确的图像先验或没有退化方法的相似模型情况下(注意前提),使用干净数据训练的模型的。
在实际上,作者仅仅基于噪声数据去学习一个单独的模型,目标是学习相机图片噪声的移除,合成蒙特卡罗图像去噪,和欠采样MRI 扫描的重构。这些图像都被不同的处理方式破坏了。
论文简介
从损坏或者不完整的测量中重建信号是统计数据分析一个重要的子领域。深度神经网络的最新进展激发了人们对避免信号损坏的传统、显式先验统计建模的浓厚兴趣,而是学习将损坏的观察结果映射到未观察到的干净版本。
训练数据可能是同一场景的短曝光和长曝光图像对,可能是磁共振图像在K空间采样完整和不完整的对,可能是光线追踪渲染合成场景下快但有噪声和慢但收敛好的光线追踪渲染图像等。
最近有多项应用方向取得了巨大进展,包括高斯去噪,去JPEG,文字移除,超分辨率,着色(colorization)和图像修复等。但是,获得干净的训练目标通常是困难或乏味的:一个没有噪声的照片需要长曝光才能获得,完整的MRI采样排除了动态对象等等。
在这项工作中,我们观察到我们通常可以通过仅查看不良图像来学习将不良图像变成良好图像,并且做得很好 - 有时甚至更好 - 就像我们使用干净的例子一样。此外,本文方法既不需要损坏的显式统计似然模型,也不需要先验图像,而是从训练数据中间接学习这些。除了去噪之外,本文的观察直接适用于逆问题,例如从欠采样数据重建 MRI。
理论背景
有监督训练前置知识
当有样本对(可靠的 x x x和 y y y)的时候,神经网络的优化目标为 arg min θ ∑ i L ( f θ ( x ^ i ) , y i ) (1) \argmin\limits_{\theta}\sum\limits_{i}L(f_{\theta}(\hat{x}_i),y_i) \tag{1} θargmini∑L(fθ(x^i),yi)(1)
假设符号 y = { y 1 , y 2 , y 3 } y=\{y1, y2, y3\} y={y1,y2,y3}为不靠谱的测量结果,比如室内温度。一个估计真实未知温度 z z z的通用策略是通过一个损失函数 L L L,寻找和测量值有最小平均偏差的温度值: arg min z E { L ( z , y ) } (2) \argmin\limits_z\mathbf{E}\{L(z,y)\} \tag{2} zargminE{L(z,y)}(2)
对于 L 2 L_2 L2损失 L ( z , y ) = ( z − y ) 2 L(z,y)=(z-y)^2 L(z,y)=(z−y)2,公式 ( 2 ) (2) (2)的最小数值为其观察列表的算数平均值: z = E y { y } (3) z=\mathbf{E}_y\{y\} \tag{3} z=Ey{y}(3)
而对于 L 1 L_1 L1损失 L ( z , y ) = ∣ z − y ∣ L(z,y)=|z-y| L(z,y)=∣z−y∣,公式 ( 2 ) (2) (2)则是寻找观察列表的中位数。
训练神经网络回归是这种点估计的推广。观察经典的训练任务形式:给定一组输入-目标对 ( x i , y i ) (x_i, y_i) (xi,yi),优化神经网络函数的参数 θ \theta θ: arg min θ E ( x , y ) { L ( f θ ( x ) , y ) } (4) \argmin\limits_{\theta}\mathbf{E}(x,y)\{L(f_{\theta(x),y})\} \tag{4} θargminE(x,y){L(fθ(x),y)}(4)
完成的训练任务可以解耦成对每个训练采样进行相同的最小化问题,简单地将下面公式 ( 5 ) (5) (5)等价于公式 ( 4 ) (4) (4): arg min θ E x { E y ∣ x { L ( f θ ( x ) , y ) } } (5) \argmin\limits_{\theta}\mathbf{E}_x\{\mathbf{E}_{y|x}\{L(f_{\theta}(x),y)\}\} \tag{5} θargminEx{Ey∣x{L(fθ(x),y)}}(5)
理论上,网络可以通过为每个输入样本单独解决点估计问题来最小化这种损失。 因此,潜在损失的属性由神经网络训练继承。(即 L 1 L1 L1寻找中位数的属性, L 2 L2 L2寻找平均数的属性)
无监督训练推理知识
文中有提到,在超分、去噪之类的病态问题上,由于一张输入图对应的是多种可能性,使用L2损失会由于导致模糊(各种可能性的平均),所以有的工作会使用学习鉴别器函数来作为损失。但是,作者发现,L2损失带来的这种平均问题的趋势,可以带来一个想不到的优势。
而作者的观察是,在一些特定问题的上,这些趋势能带来意想不到的好处(比如 L 2 L_2 L2寻找平均值得趋势)。直观来看, L 2 L_2 L2最小化的属性是寻找期望值。那么,如果我们用期望与目标匹配的随机数替换目标,这个估计值仍是不会改变的。所以,不管特殊分布 y s ys ys是怎么得出的,公式 ( 3 ) (3) (3)的结果都不会改变。相应的,如果输入的条件目标分布 p ( y ∣ x ) p(y|x) p(y∣x)也被相同期望的条件值替换,公式 ( 5 ) (5) (5)的优化网络参数 θ \theta θ也不会改变。这意味着,原则上,我们可以在网络学习内容(参数)不变的前提下,用零均值的噪声破坏训练目标。将这个与公式 ( 1 ) (1) (1)的被破坏输入相结合,就有了如下的经验风险最小化任务: arg min θ ∑ i L ( f θ ( x ^ i , y ^ i ) ) (6) \argmin\limits_{\theta}\sum\limits_{i}L(f_{\theta}(\hat{x}_i,\hat{y}_i)) \tag{6} θargmini∑L(fθ(x^i,y^i))(6)
上面公式的输入和输出都是在以底层为条件的情况下受到了损坏的分布(损坏分布不必一样),未被观察到的感觉目标也能推理出来 E { y ^ i ∣ x ^ i } \mathbf{E}\{\hat{y}_i|\hat{x}_i\} E{y^i∣x^i}。给定无限数据,解决方案和公式 ( 1 ) (1) (1)相同。给定有限数据,方差是目标中损坏的平均方差除以训练样本的数量(见附录)。
有趣的是,以上都不依赖于损坏的似然模型,也不依赖于底层干净图像流形的密度模型(先验)。 也就是说,我们不需要明确的 p ( n o i s y ∣ c l e a n ) p(noisy|clean) p(noisy∣clean) 或 p ( c l e a n ) p(clean) p(clean),只要我们有根据它们分布的数据。
应用样例
在图像恢复任务重,受损坏输入数据的期望是寻求恢复的干净目标。
比如,在低光图像重,一个长时的,没噪声的曝光是短暂的,独立的,有噪声曝光的平均值。考虑到这一点,以上内容表明仅给定噪声图像对就可以学习消除光子噪声的能力,而无需潜在的昂贵或困难的长时间曝光。
在其他损失函数上也能有相似的观察。
比如,
L
1
L_1
L1损失是恢复目标的中位数,意味着神经网络可以训练来修复具有显著离群值的内容(最高50%,因为是中位数,所以中位数得在正常范围上)。所以,也只需要成对的此类损坏图像。
论文实验
论文实验室对上面理论的实践。先从简单的噪声分布(高斯,泊松,伯努利)开始,然后进行难度更大,难以分析的蒙特卡罗图像合成噪声实验。也有实验表明能通过仅仅使用损坏的观察中学习磁共振成像 (MRI) 中亚奈奎斯特光谱采样的图像重建。
加性高斯噪声
作者使用合成加性高斯噪声研究损坏目标的影响。 由于噪声的均值为零,作者使用 L 2 L_2 L2 损失进行训练以恢复均值。
使用的baseline网络是“RED30”(Mao et al., 2016),该网络是有128层特征层的分层残差网络,被证明在广泛的图像恢复任务中有效,也包括高斯噪声。训练参数为:数据集为ImageNet中的50K张图像,patchSize为256,随机噪声标准差范围为 σ ∈ [ 0 , 50 ] \sigma\in[0,50] σ∈[0,50],噪声对每个训练样本应用。比如,网络需要在移除噪声的同时估计噪声的大小(“盲”去噪,“blind” denoising)。
验证集为BSD300,SET14和KODAK。表现如下表所示:

分析
这三个数据集上的表现在性质上是相似的,所以下面讨论平均值。使用干净的目标和标准管道训练,在
σ
=
25
\sigma=25
σ=25时,RED30达到
31.63
±
0.02
31.63 \pm 0.02
31.63±0.02dB。当目标图像使用噪声图时(公式
(
6
)
(6)
(6)),去噪的表现仍然很好。收敛速度也很快,如下图所示。所以,我们得出一个结论:在这项任务中,干净的目标不是必要的。这个结论也适用于不同的网络以及不同网络容量。作者进行了进一步测试,使用狭窄的U-Net替换了RED30,大概带来10倍的训练加速,也得到了相近的结果(高斯噪声实验中减少了0.2dB),附录中有网络架构和训练参数的描述。

收敛速度
很显然,每个训练样本要训练的要求都是不可能的。因为一个网络没有办法成功从一个噪声实例转换成另一个噪声实例。所以,训练损失在训练中也不会减少,该损失梯度仍会保持相当大。
那为什么更大、更嘈杂的梯度没有影响收敛速度呢?
虽然激活梯度确实很嘈杂,但权重梯度实际上相对干净。因为高斯噪声在所有像素中都是独立且同分布的(i.i.d,independent and identically distributed),权重梯度在整个卷积网络的
2
16
2^{16}
216个像素中进行了平均。
上图1b通过向噪声引入像素间相关性使情况变得更加困难。这种棕色加性噪声是通过不同贷款和缩放保持 σ = 25 \sigma=25 σ=25的空间高斯滤波器获得的模糊白高斯噪声。结果也如图1b所示,随着相关性的增加,权重梯度的有效平均值在减少,权重更新变得更加嘈杂(波动)。这波动让收敛变慢,但及时在极度模糊的情况下,最终画质也是相似的(在0.1db以内)。
有限数据和获取预算
以前的研究都是通过向干净图像增加合成噪声的方式获得无限的噪声示例。我们现在在有限数据和固定捕获预算的现实场景中研究损坏与干净的训练数据。
实验步骤如下。将一张ImageNet的图像添加
σ
=
25
\sigma=25
σ=25的白色加性高斯噪声对应一个捕获单元(CU,capture unit)。假设19个CU足以进行干净捕获,那么一个噪声实现加上干净版本(19个噪声实现的平均),总共消耗20个CU。整个捕获预算则定为
2000
2000
2000CUs。这个预算是通过干净的潜伏(latents)
N
N
N和每个干净潜伏的噪声实现
M
M
M得到的,即
N
∗
M
=
2000
N*M=2000
N∗M=2000。
在传统的场景中,我们只有100个图像对(
N
=
100
,
M
=
20
N=100,M=20
N=100,M=20):一个噪声实现和对应的干净图像(是19个噪声图像的平均),对应的是上图1c的Case 1。然后,作者发现使用相同的捕获数据,但使用更多的训练对方式(应该是对数据再进行噪声吧?),即
100
∗
20
∗
19
=
38000
100 * 20 * 19=38000
100∗20∗19=38000个图像对能获得更好的结果(增加0.1以上的dB),即使
N
N
N仍为
100
100
100,对应的是上图1c的Case 2。最后,作者观察到,在
N
=
1000
N=1000
N=1000,
M
=
2
M=2
M=2的设置下,即增加干净数据,但对每个数据只进行两组噪声实现,能产生更好的结果。再次增加了0.1以上的db,上图1c的Case 3.
结论:对于加性高斯噪声,对比干净的目标,损坏的目标在两个层面上提供好处,不仅性能相同,而且更好。两个好处为:(1)可以看到相同潜在干净图像的更多损坏实现;(2)可以看到更多潜在的干净的图像,即使每个图像只有两个损坏的实现,那也是有益的。
我们得出结论,对于加性高斯噪声,损坏的目标在两个层面上比干净的目标提供好处——不仅性能相同,而且更好:两者都是 1) 看到相同潜在干净图像的更多损坏实现,以及 2) 看到更多潜在的 干净的图像,即使每个图像只有两个损坏的实现,也是有益的。
结果展示
下面展示了一些RED30的结果:




其他合成噪声
泊松噪声
泊松噪声是图片噪声的主要来源。尽管泊松噪声是零均值,因为它是信号依赖的,所以它更难以去除。训练时,使用 L 2 L_2 L2损失,噪声强度范围为 λ ∈ [ 0 , 50 ] \lambda\in[0,50] λ∈[0,50]。使用干净数据目标的结果在 30.59 ± 0.02 30.59\pm0.02 30.59±0.02dB,而噪声数据目标也相当好,在 30.57 ± 0.02 30.57\pm0.02 30.57±0.02dB,也是相似的收敛速度。
对比的方式为:先使用Anscombe 转换将泊松噪声转换成高斯噪声,然后通过BM3D去噪,再进行逆转换。得到的结果比本文方法少2dB。
其他效应,例如暗电流和量化,由泊松噪声主导,可以设为零均值(Hasinoff 等人,2016 年),因此不会对噪声目标的训练造成任何问题。
我们得出结论,在此应用程序中不需要无噪声训练数据。
乘性伯努利噪声
乘性伯努利噪声,又名二项式噪声。构造一个随机掩码 m m m,其数值 1 1 1表示有效像素,数值 0 0 0表示置零/丢失像素。为了避免丢失像素也进行梯度的反向传播,所以将其排除在损失计算中:这我就不懂了,丢失的像素不是才要得到的吗? arg min θ ∑ i ( m ⊙ ( f θ ( x ^ i ) − y ^ i ) ) 2 (7) \argmin\limits_{\theta}\sum\limits_{i}(m\odot(f_{\theta}(\hat{x}_i)-\hat{y}_i))^2 \tag{7} θargmini∑(m⊙(fθ(x^i)−y^i))2(7)
损坏像素的概率被 p p p定义,在训练中, p p p的范围为 p ∈ [ 0.0 , 0.95 ] p\in[0.0,0.95] p∈[0.0,0.95],测试时, p = 0.5 p=0.5 p=0.5。使用干净数据,训练结果均值在 31.85 ± 0.03 31.85\pm0.03 31.85±0.03dB,噪声数据有一点提升,在 32.02 ± 0.03 32.02\pm0.03 32.02±0.03dB。可能是因为嘈杂的目标在网络输出端有效地实现了一种 dropout 形式 (Srivastava et al., 2014)。DIP要差2dB左右。DIP不是基于机器学习的解决方案,也与本文的方法非常不同,但它的特点是不需要干净样本,也不需要明确的损坏模型。本文使用了 DIP 补充材料中描述的“图像重建”设置。
文字清除
下图3展示了盲文本清除的结果。损坏包括随机位置的大量不同数量的随机字符串,它们也彼此重叠,而且字体大小和颜色也是随机的。字体和字符串方向保持不变。

该网络使用独立损坏的输入和目标对进行训练。损坏像素的概率 p p p在训练时调整范围为 p ∈ [ 0 , 0.5 ] p\in[0,0.5] p∈[0,0.5],在测试时 p ≈ 0.25 p\approx 0.25 p≈0.25。
在实验中,发现 L 2 L_2 L2损失对该任务不是正确选项。因为覆盖的文本具有与实际图像无关的颜色,并且生成的图像会错误地倾向于正确答案和平均文本颜色(中灰色)的线性组合。然而,对于任何合理数量的重叠文本(小于0.5的遮盖),一个像素往往会保留原始颜色,因此中位数是正确的统计数据。故使用 L 1 = ∣ f θ ( x ^ − y ^ ) ∣ L_1=|f_\theta(\hat{x}-\hat{y})| L1=∣fθ(x^−y^)∣作为损失函数。上图表现了一个样例结果。
随机值脉冲噪声
随机值脉冲噪声用噪声替换一些像素并保留其他像素的颜色。作者研究的不是标准的椒盐噪声(用黑色或白色随机替换像素),而是研究更难的分布,其中每个像素都替换为从概率为 p p p的均匀分布 [ 0 , 1 ] 3 [0,1]^3 [0,1]3中抽取的随机颜色,概率 1 − p 1-p 1−p为保留原始颜色。像素的颜色分布是原始颜色的狄拉克分布加上均匀分布,相对权重由替换概率 p 给出。在这个事例中,均值和中值都不能产生正确结果。期望目标是一个分布模式(Dirac spike)。分布仍然是单峰的。对于近似模式搜索,我们使用定义为“L0 损失”函数的退火版本 ( f θ ( x ^ ) − y ^ + ϵ ) γ (f_\theta(\hat{x})-\hat{y}+\epsilon)^\gamma (fθ(x^)−y^+ϵ)γ,其中 ϵ = 1 0 − 8 \epsilon=10^{-8} ϵ=10−8, γ \gamma γ在训练过程中从 2 2 2线性退火到 0 0 0。这种退火不会在本文的测试中引起任何数值问题。 附录分析了L0损失与寻模的关系。
训练网络时,同样使用噪声输入和噪声输出,损坏像素的概率对于每个对都在
[
0
,
0.95
]
[0,0.95]
[0,0.95]中随机设置。图 4 显示了 70% 输入像素被随机化时的推理结果。使用 L2 损失进行训练会使结果严重偏向灰色,因为结果倾向于线性组合正确答案和均匀随机损坏的均值。正如理论预测的那样,只要少于 50% 的像素被随机化,L1 损失就会产生良好的结果,但超过该阈值后,它会很快开始使暗区和亮区偏向灰色(下图 5)。另一方面,即使在极度损坏(例如 90% 像素)的情况下,L0 也显示出很小的偏差,因为所有可能的像素值,正确答案(例如 10%)仍然是最常见的。


蒙塔卡罗渲染
高动态范围(HDR)
蒙塔卡罗渲染图像去噪
磁共振成像 (MRI)
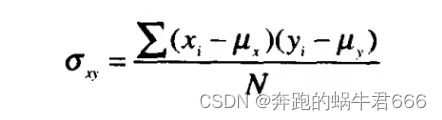


![[附源码]Python计算机毕业设计Django-中国传统手工艺销售平台](https://img-blog.csdnimg.cn/8ef98439179a44118e1285446de01e50.png)



![[附源码]Python计算机毕业设计Django在线影院系统](https://img-blog.csdnimg.cn/96950f8b6b57476cbfb3b57398eee355.png)
![[附源码]计算机毕业设计JAVA中小学微课学习系统](https://img-blog.csdnimg.cn/c08e2fb567794d0b82fffb3eebdc2247.png)