Problem - 1340B - Codeforces

 

Denis,在买了花和糖果之后（你将在下一个任务中了解这个故事），与Nastya约会，向她表白要成为一对。现在，他们坐在咖啡馆里，最后... Denis请她答应在一起，但是... Nastya没有给出任何答案。

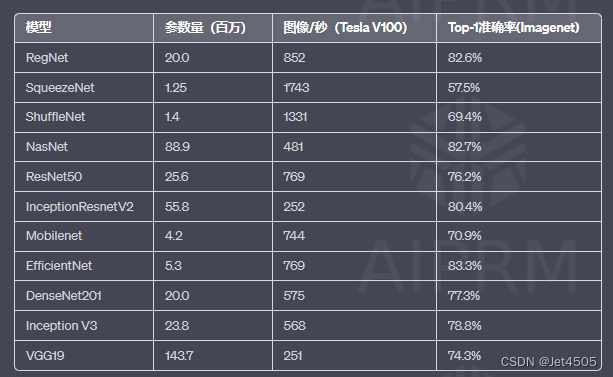
因此，这个可怜的男孩非常难过。他非常伤心，以至于用拳头砸了一个带有数字的记分牌。数字显示方式与电子时钟相同：每个数字位置由7个段组成，可以打开或关闭以显示不同的数字。图片展示了如何显示所有10个十进制数字：

打击后，一些段停止工作，也就是说，一些段可能会停止发光，如果它们之前发光的话。但是Denis记得有多少根杆子亮着，现在又有多少根杆子亮着。Denis打破了恰好k个段，他知道哪些杆子现在还能工作。Denis提出了问题：如果你打开恰好k个目前关闭的杆子，最大可能出现在记分牌上的数字是多少？

允许数字包含前导零。

输入

第一行包含整数n（1≤n≤2000）- 记分牌上的数字数量和k（0≤k≤2000）- 停止工作的段数量。

接下来的n行包含长度为7的二进制字符串，其中第i个字符串编码了记分牌上的第i个数字。

记分牌上的每个数字由7个段组成。我们按照下图的方式对它们编号，并假设二进制字符串的第i位如果第i根杆不发光，则为0，如果发光，则为1。因此，长度为7的二进制字符串将指定当前发光的段。

因此，序列“1110111”，“0010010”，“1011101”，“1011011”，“0111010”，“1101011”，“1101111”，“1010010”，“1111111”，“1111011”依次编码从0到9的所有数字。

输出

输出一个由n个数字组成的单个数字 - 如果你打开恰好k根杆子，可以得到的最大数字；如果无法打开恰好k根杆子以显示正确数字，则输出-1。

示例

输入 拷贝

1 7

0000000

输出 拷贝

8

输入 拷贝

2 5

0010010

0010010

输出 拷贝

97

输入 拷贝

3 5

0100001

1001001

1010011

输出 拷贝

-1

注意

在第一个测试中，我们必须包括所有7根杆，并在记分牌上得到一个8。

在第二个测试中，我们打开了一些杆子，以形成数字。对于额外包括的5根杆，可以得到数字07、18、34、43、70、79、81和97，我们选择最大值-97。

在第三个测试中，无法只打开5根杆以显示记分牌上的数字序列。

题解:
首先我们,对于每串数字,可以看他都可以变成什么数字,花费是多少

如果一串数字,无法变成任何0~9的数字,直接输出-1即可(这种情况出现的原因是,原本一个数字那里没有1,但是给出的串上有1)

接着我们可以根据这个花费,从末尾开始往前,记录每个位置的,最大最小花费,便于我们搜索时剪枝

接着从第一位进行搜索,每一位搜索的过程都应该时9~0,

因为贪心来讲,我们如果要结果最大,肯定让前面的数字越大越好,即使他需要消耗的更多,并且这样搜索,会导致第一次搜索成功就是最大值

如果我们搜完恰好用了k次,记得都要返回

搜索过程中,除了根据每个位置我们记录的最大,最小值进行剪枝,还要根据,每个位置的花费看是否成功进行剪枝

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
 #define int long long
typedef pair<int,int> PII;
typedef unsigned long long ULL;
const int N = 5e5 + 10;
int mod = 1e9 + 7;
int n,k;
int vis[2004][30];
string a[11]={ "1110111", "0010010", "1011101", "1011011", "0111010", "1101011", "1101111", "1010010", "1111111", "1111011" };
int ma[N],mi[N];
int st;
int ans[2004];
int dp[2002][2002];
void dfs(int now,int hua)
{
	if(now == n + 1)
	{
		if(hua == k)
		{
			st = 1;
		}
		return ;
	}
	if(st)
	return ;
	if(dp[now][hua] == -1)
	return ;
	for(int i = 9;i >= 0;i--)
	{
		if(vis[now][i] == -1)
		continue;
		if(hua + vis[now][i] > k)
		continue;
		int els = k - hua - vis[now][i];
		if(els > ma[now + 1])
		continue;
		if(els < mi[now + 1])
		continue;
		ans[now] = i;
		dfs(now + 1,hua + vis[now][i]);
		if(st)
		return ;
		dp[now][hua] = -1;
	}
}
int check(string s,string t)
{
	int w = 0;
	for(int i = 0;i < 7;i++)
	{
		if(s[i] == '1'&&t[i] == '0')
		{
			return -1;
		}
		else if(s[i] != t[i])
		{
			w++;
		}
	}
	return w;
}
void solve()
{
	cin >> n >> k;
	int flag = 0;
	for(int i = 1;i <= n;i++)
	{
		string s;
		cin >> s;
		int f = 0;
		for(int j = 0;j <= 9;j++)
		{
			vis[i][j] = check(s,a[j]);
			if(vis[i][j] != -1)
			{
				f = 1;
			}
		}
		if(!f)
		{
			flag = 1;
		}
	}
	if(flag)
	{
		cout <<"-1\n";
		return ;
	}
	for(int i = n;i >= 1;i--)
	{
		int Max = 0,Min = 1e9;
		for(int j = 0;j <= 9;j++)
		{
			if(vis[i][j] == -1)
			continue;
			Max = max(Max,vis[i][j]);
			Min = min(Min,vis[i][j]);
		}
		ma[i] = ma[i + 1] + Max;
		mi[i] = mi[i + 1] + Min;
	}
	dfs(1,0);
	if(!st)
	{
		cout <<"-1";
		return ;
	}
	for(int i = 1;i <= n;i++)
	{
		cout << ans[i];
	}
}
signed main()
{
	ios::sync_with_stdio(0 );
	cin.tie(0);cout.tie(0);
	int t = 1;
//	cin >> t;
	while(t--)
	{
		solve(); 
	}
}