常用数据预处理与特征选择方法总结记录

在很多机器学习或者是深度学习建模之前，对于数据的处理尤为重要，选择合适的数据预处理方法和特征构建算法对于后续模型的结果有着很大的影响作用，这里的主要目的就是想记录总结汇总常用到的处理方法，学习备忘！

数据清洗：
数据清洗是指对数据进行处理，以去除或修正缺失值、异常值和重复值等问题。
   处理缺失值：
   可以通过删除包含缺失值的样本、使用均值或中位数填充缺失值，或使用插值方法（如线性插值或多重插补）来填充缺失值。
   优点：
   简单易行，不会引入额外的特征。
   缺点：
   可能会导致数据丢失或引入不准确性，填充方法可能不适用于所有情况。

   处理异常值：
   可以通过统计方法（如3σ原则）或使用离群点检测算法（如箱型图或基于距离的方法）来识别和处理异常值。
   优点：
   可以排除异常值对模型造成的干扰。
   缺点：
   可能会误删有用的信息，需要专业领域知识来判断异常值是否真实存在。

   处理重复值：
   可以通过比较样本之间的特征值，找出并删除重复的记录。
   优点：
   避免了重复数据对模型训练和评估的影响。
   缺点：
   删除重复值可能会减少数据集的大小，但在某些情况下可能没有太大影响。

Demo代码实现如下所示：

import numpy as np
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor
from sklearn.datasets import make_classification


"""
使用make_classification生成了一个具有缺失值、异常值和重复值的示例数据集。然后，分别使用SimpleImputer进行缺失值填充、使用IsolationForest进行异常值检测和移除、使用np.unique进行重复值去除
"""


# 创建一个示例数据集
X, y = make_classification(n_samples=100, n_features=5, n_informative=3, n_classes=2, random_state=42)

# 处理缺失值
missing_values = np.isnan(X)
imputer = SimpleImputer(strategy='mean')  # 使用均值填充缺失值，也可以使用'median'或'most_frequent'
X_filled = imputer.fit_transform(X)

# 处理异常值
outlier_detector = IsolationForest(contamination=0.1)  # 设置异常值比例为10%
outlier_labels = outlier_detector.fit_predict(X_filled)
X_outliers_removed = X_filled[outlier_labels == 1]

# 处理重复值
_, unique_indices = np.unique(X_outliers_removed, axis=0, return_index=True)
X_duplicates_removed = X_outliers_removed[np.sort(unique_indices)]

特征缩放：
特征缩放是对特征进行归一化或标准化，以使其具有相同的尺度。
   归一化：
   将特征值缩放到0和1之间，常用方法包括最小-最大规范化。
   优点：
   保留了特征的分布形状，适用于对特征值范围敏感的算法（如K近邻）。
   缺点：
   可能受极端值的影响，对离群点不稳定。

   标准化：
   将特征值转换为均值为0、方差为1的正态分布，常用方法包括Z-score标准化。
   优点：
   更稳定，不受极端值的影响。
   缺点：
   可能会改变特征的分布形状。

Demo代码实现如下所示：

import numpy as np
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.datasets import make_classification


"""
使用make_classification生成了一个示例数据集。然后，分别使用MinMaxScaler进行归一化和使用StandardScaler进行标准化。

在归一化中，MinMaxScaler将特征值缩放到0和1之间，通过选择最小值和最大值来确定缩放范围。优点是保留了特征的分布形状，适用于对特征值范围敏感的算法（如K近邻）。缺点是可能受极端值的影响，对离群点不稳定。

在标准化中，StandardScaler将特征值转换为均值为0、方差为1的正态分布。优点是更稳定，不受极端值的影响。缺点是可能会改变特征的分布形状。
"""

# 创建一个示例数据集
X, y = make_classification(n_samples=100, n_features=5, n_informative=3, n_classes=2, random_state=42)

# 归一化
minmax_scaler = MinMaxScaler()
X_normalized = minmax_scaler.fit_transform(X)

# 标准化
standard_scaler = StandardScaler()
X_standardized = standard_scaler.fit_transform(X)

数据平衡：
数据平衡处理是针对不平衡的分类问题，通过过采样、欠采样或合成新样本等方法来调整类别之间的样本数量差异。
   过采样：
   增加少数类样本的数量，常用方法有随机复制、SMOTE（合成少数类过采样技术）等。
   优点：
   可以提高模型对少数类的识别能力。
   缺点：
   可能导致过拟合，并引入重复信息。

   欠采样：
   减少多数类样本的数量，常用方法有随机删除、Tomek Links等。
   优点：
   可以提高模型对多数类的泛化能力。
   缺点：
   可能会导致丢失多数类的重要信息。

   合成新样本：
   通过利用少数类和多数类之间的关系来合成新的样本，例如SMOTE。
   优点：
   保留了原始数据分布的特征，避免了信息丢失。
   缺点：
   可能引入合成样本的噪声。

Demo代码实现如下所示：

import numpy as np
from sklearn.datasets import make_classification
from sklearn.utils import resample
from imblearn.over_sampling import SMOTE

"""
使用make_classification生成了一个示例的不平衡数据集。然后，使用resample函数进行过采样和欠采样。对于过采样，我们随机复制了少数类样本，使其数量与多数类相同。对于欠采样，我们随机从多数类样本中删除了一些样本，使其数量与少数类相同。最后，使用SMOTE进行合成新样本，根据少数类和多数类之间的关系生成新的样本。
"""

# 创建一个示例不平衡的数据集
X, y = make_classification(n_samples=1000, n_features=10, weights=[0.9, 0.1], random_state=42)

# 过采样
X_oversampled, y_oversampled = resample(X[y == 1], y[y == 1], replace=True,
                                        n_samples=X[y == 0].shape[0], random_state=42)
X_balanced_oversampled = np.concatenate((X[y == 0], X_oversampled))
y_balanced_oversampled = np.concatenate((y[y == 0], y_oversampled))

# 欠采样
X_undersampled, y_undersampled = resample(X[y == 0], y[y == 0], replace=False,
                                          n_samples=X[y == 1].shape[0], random_state=42)
X_balanced_undersampled = np.concatenate((X[y == 1], X_undersampled))
y_balanced_undersampled = np.concatenate((y[y == 1], y_undersampled))

# 合成新样本
smote = SMOTE(random_state=42)
X_synthetic, y_synthetic = smote.fit_resample(X, y)

数据转换：
数据转换是对数据进行转换，以满足模型假设或改善数据的分布。
   对数转换：
   将数据取对数，常用于偏态分布的数据。
   优点：
   可以使数据更加对称，减小极端值的影响。
   缺点：
   无法处理非正值或零值。

   指数转换：
   将数据进行指数变换，常用于数据呈指数增长的情况。
   优点：
   可以减小指数增长带来的差异性，使得模型更容易捕捉到趋势。
   缺点：
   可能会放大噪声，造成数据的不稳定性。

Demo代码实现如下所示：

import numpy as np
from sklearn.preprocessing import FunctionTransformer
from sklearn.datasets import make_classification


"""
使用make_classification生成了一个示例数据集。然后，分别使用FunctionTransformer进行对数转换和指数转换。

对于对数转换，np.log1p函数将数据取对数（以e为底），np.expm1函数为其逆操作。这种转换常用于偏态分布的数据，可以使数据更加对称，减小极端值的影响。

对于指数转换，np.exp函数将数据进行指数变换（以e为底），np.log函数为其逆操作。这种转换常用于数据呈指数增长的情况，可以减小指数增长带来的差异性，使得模型更容易捕捉到趋势。
"""


# 创建一个示例数据集
X, y = make_classification(n_samples=100, n_features=5, n_informative=3, n_classes=2, random_state=42)

# 对数转换
log_transformer = FunctionTransformer(func=np.log1p, inverse_func=np.expm1)
X_log_transformed = log_transformer.transform(X)

# 指数转换
exp_transformer = FunctionTransformer(func=np.exp, inverse_func=np.log)
X_exp_transformed = exp_transformer.transform(X)

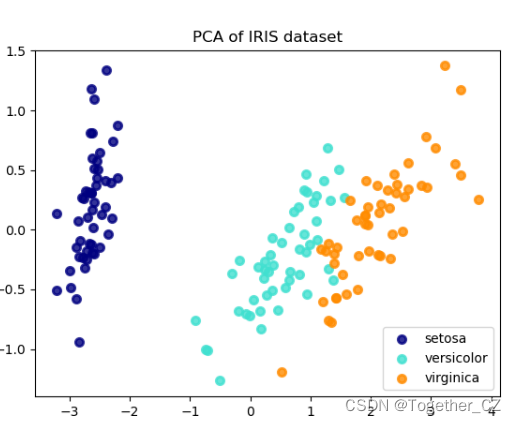
降维：
降维是通过减少特征维度来降低数据复杂性和噪声的方法。
   主成分分析（PCA）：
   通过线性变换将原始特征映射到新的特征空间，以保留最大方差的主成分。
   优点：
   可以消除高度相关的特征，并减少数据集的维度。
   缺点：
   可能导致信息丢失，不适用于非线性关系的问题。

   线性判别分析（LDA）：
   在保持类别间距离最大化和类别内距离最小化的基础上，将高维数据投影到低维空间。
   优点：
   可以减少维度同时保持类别信息。
   缺点：
   对数据的分布假设要求较高。

Demo代码实现如下所示：

import numpy as np
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification


"""
使用make_classification生成了一个示例数据集。然后，分别使用PCA进行主成分分析和LinearDiscriminantAnalysis进行线性判别分析。

主成分分析（PCA）通过线性变换将原始特征映射到新的特征空间，在保留最大方差的前K个主成分的基础上实现降维。优点是可以消除高度相关的特征，并减少数据集的维度。缺点是可能导致信息丢失，不适用于非线性关系的问题。

线性判别分析（LDA）在保持类别间距离最大化和类别内距离最小化的基础上，将高维数据投影到低维空间。优点是可以减少维度同时保持类别信息。缺点是对数据的分布假设要求较高。
"""



# 创建一个示例数据集
X, y = make_classification(n_samples=100, n_features=10, n_informative=5, n_classes=2, random_state=42)

# 主成分分析（PCA）
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)

# 线性判别分析（LDA）
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X, y)