文章目录
- 1. 什么是汉诺塔
- 2. 汉诺塔的解题步骤
- 3. 代码实现汉诺塔
1. 什么是汉诺塔
1. 汉诺塔的来源
一位法国数学家曾编写过一个印度的古老传说:在世界中心拿勒斯的圣庙里边,有一块黄铜板,上边插着三根宝柱。印度教的主神梵天在创造世界的时候,在其中一根柱从下到上穿好了 64 片金片,这就是所谓的汉诺塔。然后不论白天黑夜,总有一名僧侣按照下面的法则来移动这些金片:一次只移动一片,不管在哪根柱子上,小片必须在大片上面。
2. 汉诺塔的玩法
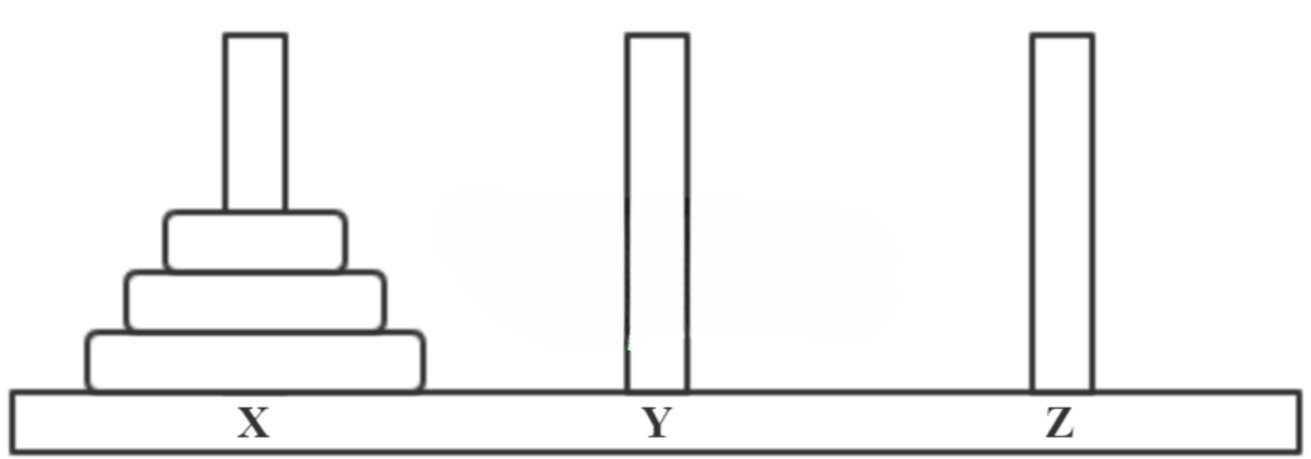
- 暂时用三层的汉诺塔来演示,初始状态下的汉诺塔如下图所示:
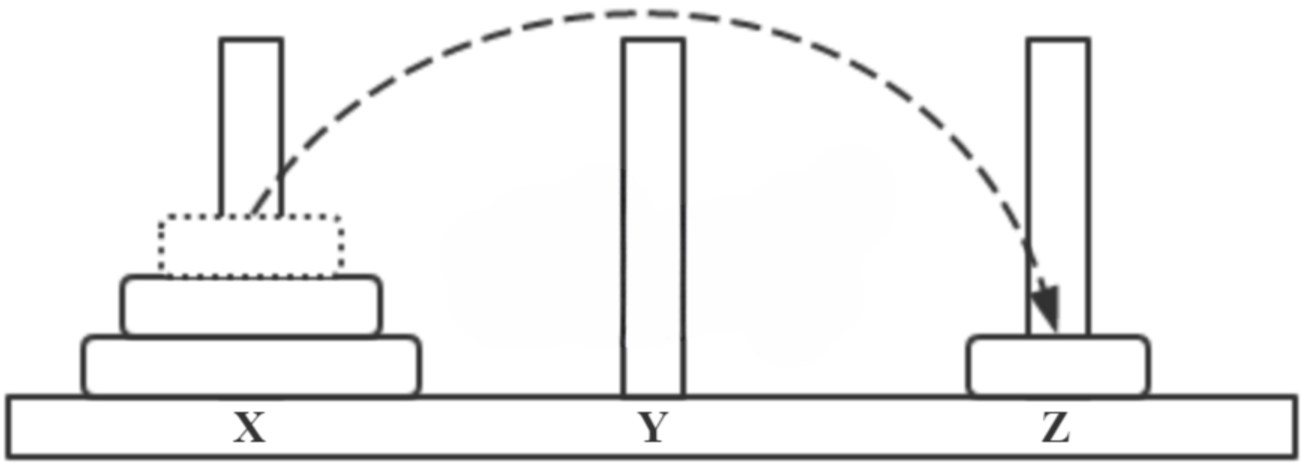
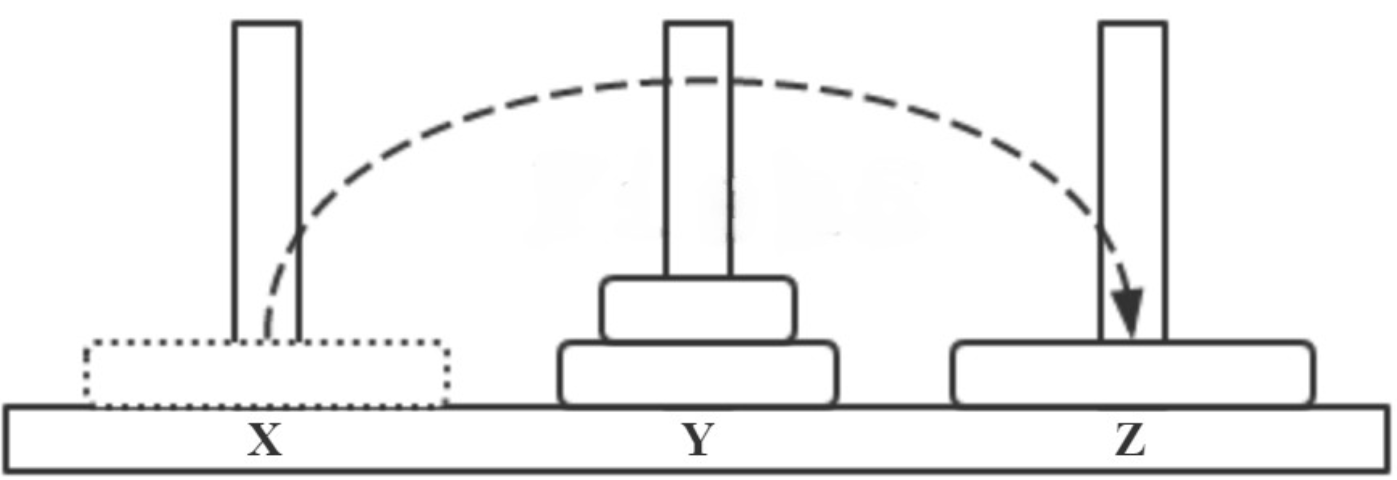
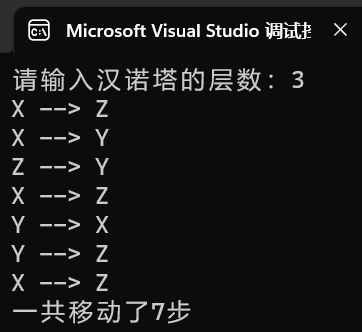
- step1 X → Z,如下图所示。
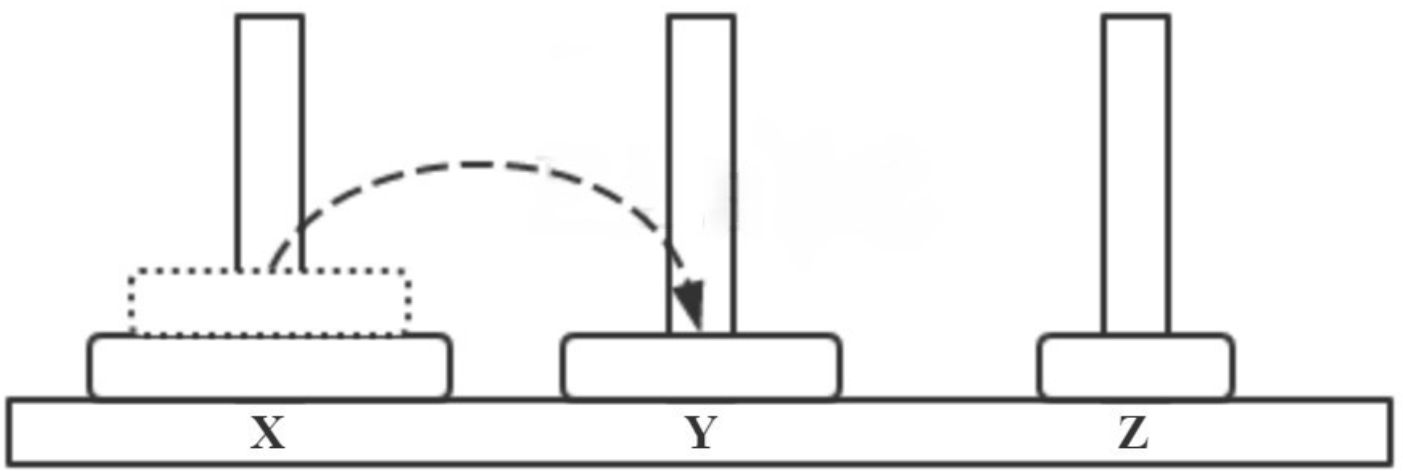
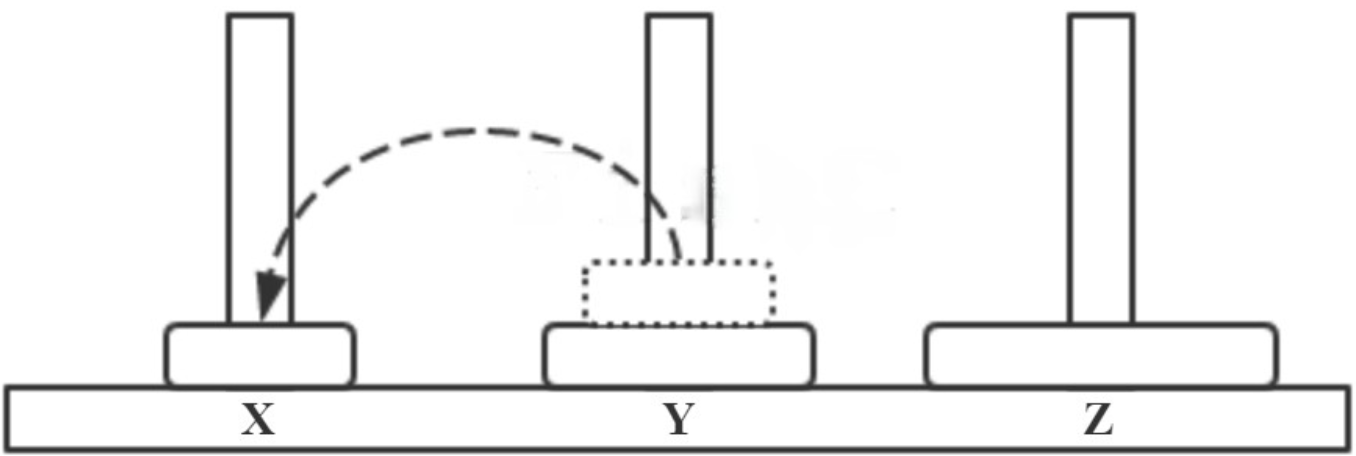
- step2 X → Y,如下图所示。
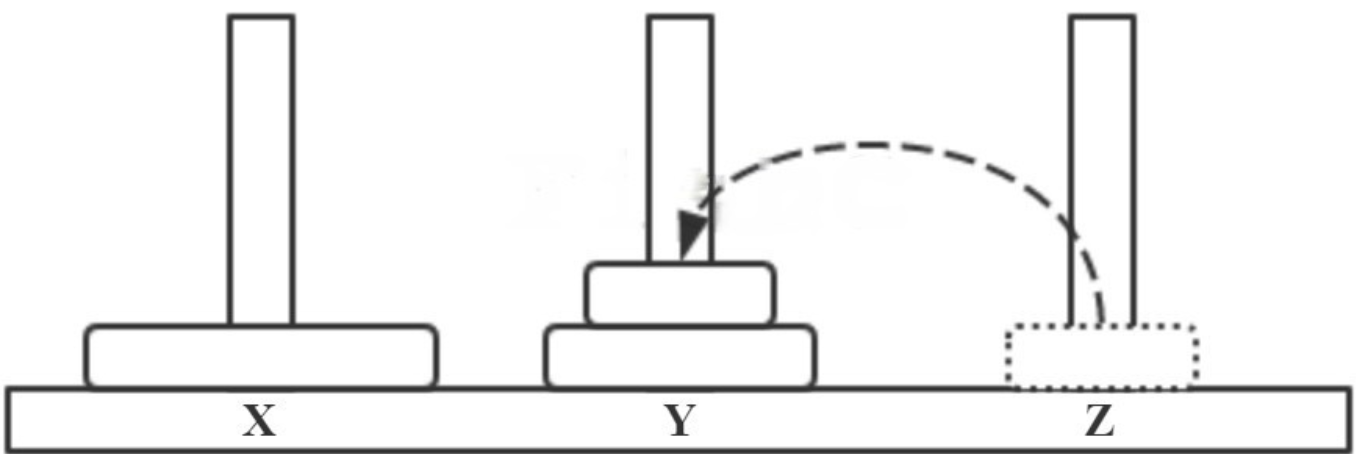
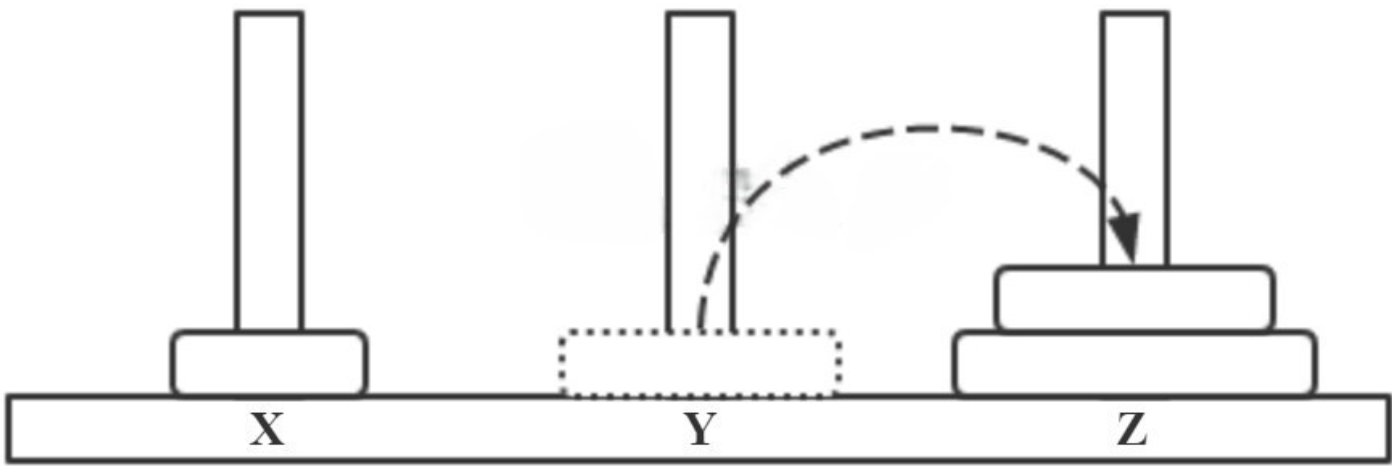
- step3 Z → Y,如下图所示。
- step4 X → Z,如下图所示。
- step5 Y → X,如下图所示。
- step6 Y → Z,如下图所示。
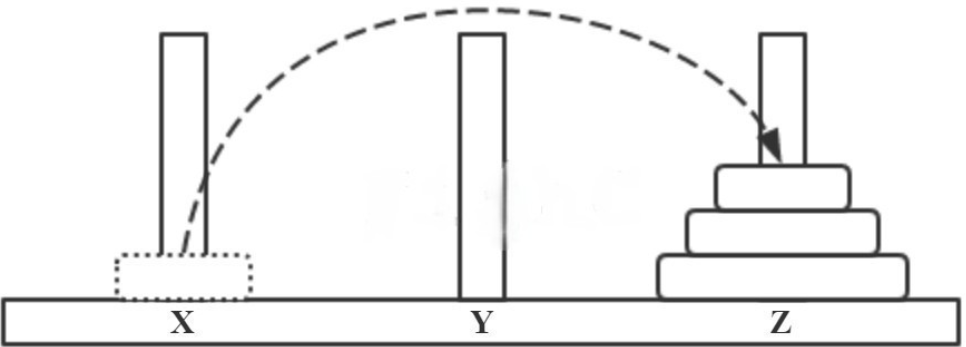
- step7 X → Z,如下图所示。
2. 汉诺塔的解题步骤
对于上述游戏的玩法,可以简单分解为以下三个步骤
- 将前 n-1 个盘子从 X 柱移动到 Y 柱上,,确保大盘在小盘下面。
- 将最下面的第 n 个盘子从 X 柱移动到 Z 柱上。
- 将 Y 柱上的 n-1 个盘子移动到 Z 柱上。
- 在游戏中,由于每次只能移动一个圆盘,所以在移动的过程中显然要借助另外一根柱子才可以实施。
- 步骤(1)将 X 柱上的 1 ~ n-1 个盘子移动到 Y 柱上,需要借助 Z 柱;
- 步骤(3)将 Y 柱上的 n-1 个盘子移动到 Z 柱上,则需要借助 X 柱。
- 所以把新的思路分成以下两个问题。
- 问题1:如何将 X 柱上的 n-1 个盘子借助 Z 柱移动到 Y 柱上?
- 问题2:如何将 Y 柱上的 n-1 个盘子借助 X 柱移动到 Z 柱上?
- 解决这两个问题的方法与解决 “ 如何将 X 柱上的 n 个盘子借助 Y 柱移动到 Z 柱上?” 这个问题是一样的,都是可以拆解成上述三个步骤来实现。
问题1:将(如何将 X 柱上的 n-1 个盘子借助 Z 柱移动到 Y 柱上?)这个问题拆解为:
- 将前 1 ~ n-2 个盘子从 X 柱移动到 Z 柱上,确保大盘在小盘下面。
- 将最底下的第 n-1 这一个盘子移动到 Y 柱上。
- 将 Z 柱上的 1 ~ n-2 个盘子移动到 Y 柱上。
问题2:将(如何将 Y 柱上的 1 ~ n-1 个盘子借助 X 柱移动到 Z 柱上?)这个问题拆解为:
- 将前 1 ~ n-2 个盘子从 Y 柱移动到 Z 柱上,确保大盘在小盘下面。
- 将最底下的第 n-1 这一个盘子移动到 Z 柱上。
- 将 X 柱上的 1 ~ n-2 个盘子移动到 Y 柱上。
3. 代码实现汉诺塔
- 汉诺塔的拆解过程刚好就满足递归算法的定义,因此,使用递归来解决汉诺塔问题就变得很简单了。
#include <stdio.h>
int count = 0;
void hanoi(int n, char x, char y, char z)
{
if (1 == n)//如果只有一层则直接将盘子从 X 移到 Z 柱即可
{
printf("%c --> %c\n", x, z);
}
else//反之则看着解题步骤去写代码
{
hanoi(n - 1, x, z, y);//步骤1:将前 n-1 个盘子借助 z 柱从 x 柱移到 y 柱
printf("%c --> %c\n", x, z);
hanoi(n - 1, y, x, z);//步骤3:将 Y 柱上的 n - 1 个盘子借助 x 柱移动到 z
}
count++;
}
int main()
{
int n;
printf("请输入汉诺塔的层数:");
scanf("%d", &n);
hanoi(n, 'X', 'Y', 'Z');//n:汉诺塔层数。X Y Z:汉诺塔的三根柱子
printf("一共移动了%d步\n", count);
return 0;
}
代码分析
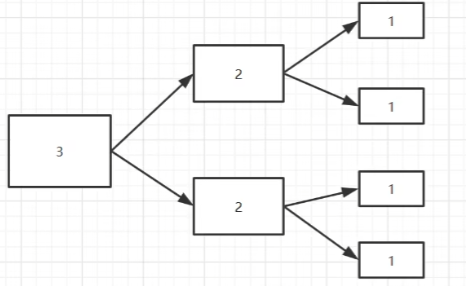
- 想要解决一个 3 层的汉诺塔,就得先解决两个 2 层的汉诺塔,要完成一个 2 层的汉诺塔又得先完成两个 1 层的汉诺塔。
- 同理,想要解决一个 n 层的汉诺塔,就得先解决两个 n-1 层的汉诺塔,解决一个 n-1 层的汉诺塔就又得先完成两个 n-2 层的汉诺塔。