1.选择排序
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。

Java代码实现如下。

ps:选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2),同时选择排序不是稳定的排序算法,选择排序只需要常量的内存空间消耗所以是原地排序算法。
2.归并排序(Merge Sort)
我们先看看归并排序的实现思路
1.先将需要比较的数组从中间进行拆分前后两部分,然后将拆完后的继续拆分成前后两部分,直到不能拆分为止,图中并非完全拆好后结果,只是第一步。

2.将每次拆分的前后两部分分别进行排序
首先我们用两个游标i和j来分别指向前部分的第一个数据和后部分的一个数据,然后比较前部分的第一个数据和后一个的第一个数据,如果前部分的第一个比后部分的第一个小,那么就将前部分的一个放入新的数组中,同时前部分游标向后移动,也就是i++,否则就是将后部分的第一个数据放入到新数组中,同时后部分游标向后移动,也就是j++。直到i和j的值为数组长度时结束。

ps:那么如果前部分已经全部放入新数组中,而后部分还有没有放入新数组中的怎么办呢?我们直接将没有放入新数组中的数据依次放入即可.

3.最后将排好序的前后部分进行合并
合并我们需要借助另一个数组来实现,也就是一个和排序数组长度相同的数组,每个分治排序后的数据都是放在新数组中,同时将新数组中的值拷贝到原数组中,使原数组中分治的左右两边都是有有序的.
Java代码实现如下。

ps:归并排序的时间复杂度为 O(nlogn),同时归并排序是稳定的排序算法,归并排序需要一个和排序数组一样大的新数组,内存空间为O(n),所以不是原地排序算法。
3.快速排序
我们来看看快速排序的实现原理,首先给数组找一个基准数,一般选择首或者尾,然后用两个游标来指向数组两头,用尾部j比较基准数k,如果基准数小于j,则j向左移动,若基准数大与j,那么j不动,同时i开始比较基准数,如果基准数大于i那么i向右移动,若基准数小于i那么此时i和j交换数据,交换后j继续比较基准数,直到最后i和j相遇时,将基准数和j互换。
然后把i的位置移动到k,缩小范围,继续将基准数k的左边变为都是小于他的数,右边都是大于他的数,数组左边全部完成后把基准数变为数组右半边第一位,继续把基准数小的移动到左边,大的在基准数右边。

Java代码实现如下。
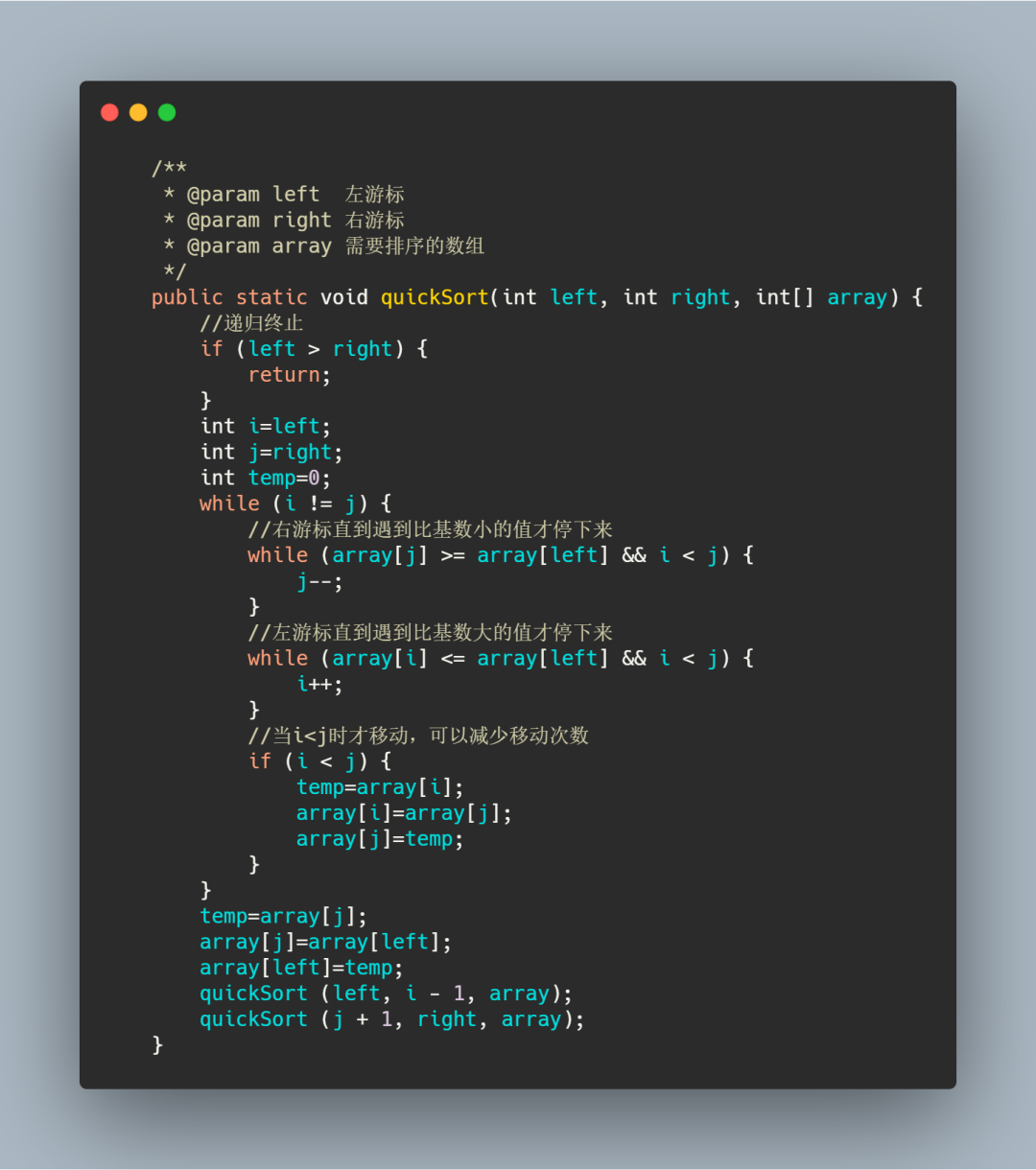
ps:快速排序时间复杂度绝大多数都是O(nlogn),但是如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。如果我们每次选择最后一个元素作为基准数,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。同时快速排序不是稳定的排序算法,快速排序只需要常量的内存空间消耗所以是原地排序算法。