题目：
给定二叉树头结点head，任何两个节点之间都有距离，求整棵二叉树最大距离。
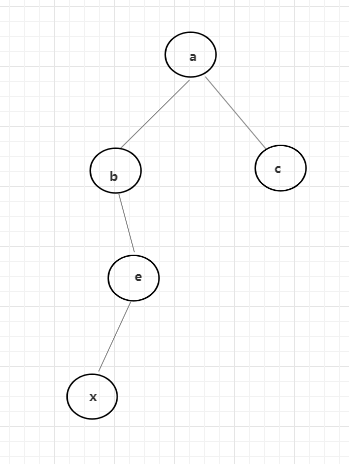
二叉树如下图所示，假设从x到b，中间节点只能走一次，我们人为规定距离就是整条路径的节点数量，所以距离是3：x -> e -> b。这棵树最大的距离是5（x - > c）。

分析：
由此可以推断出，一棵树最大的距离共有2类3种情况。一种是经过的head节点，一种是没经过head节点

1. 经过x节点，那最大距离就是左树高度+右树高度+1（head节点）
2. 没经过x节点，则可能会是左子树的最大距离，也可能是右子树的最大距离

public static class Node{
        int val;
        Node left;
        Node right;
        public Node(int val){
            this.val = val;
        }
    }
    //收集左右子树信息，树高度和最大距离
    public static class Info{
        int height;
        int maxDistinct;

        public Info(int height,int maxDistinct){
            this.height = height;
            this.maxDistinct = maxDistinct;
        }
    }

    public static int maxDistinct(Node head){
        if (head == null ){
            return 0;
        }
        return process(head).maxDistinct;
    }
		
    public static Info process(Node head){
        if (head == null){
            return new Info(0,0);
        }
		
        Info leftInfo = process(head.left);
        Info rightInfo = process(head.right);
		
        int height = Math.max(leftInfo.height,rightInfo.height) + 1;
        //一共3种情况
        //最大距离是左子树的最大距离
        int p1 = leftInfo.maxDistinct;
        //最大距离是右子树的最大距离
        int p2 = rightInfo.maxDistinct;
        //经过了head节点，那么就是左右子树的高度相加 再加上head节点的 1
        int p3 = leftInfo.height +  rightInfo.height + 1;
		//在3种情况中求得这棵树的最大距离
        int maxDistinct = Math.max(p3,Math.max(p1,p2));
        return new Info(height,maxDistinct);
    }