数学建模常用模型(四):灰色关联分析法
灰色关联分析法(Grey Relational Analysis,GRA)是一种用于多指标决策评价的方法,由灰色系统理论发展而来。它用于分析和评价多个指标之间的相关性和影响程度,帮助决策者进行综合评价和决策。
这是我自己总结的一些代码和资料(本文中的代码以及参考书籍等),放在github上供大家参考:https://github.com/HuaandQi/Mathematical-modeling.git
1.灰色关联分析法的基本步骤如下:
-
数据标准化:将原始指标数据进行标准化,使得数据在相同范围内,并消除因量纲不同而引起的影响。
-
构建关联度矩阵:根据标准化后的数据,计算各个指标之间的关联度。关联度矩阵反映了各个指标之间的相似程度。
-
确定关联度函数:根据问题的特点和需求,选择合适的关联度函数来计算指标之间的关联度。常用的关联度函数包括线性关联度函数、指数关联度函数等。
-
计算关联度系数:根据关联度函数,计算出各个指标与目标指标之间的关联度系数。关联度系数越大,表示指标与目标指标之间的关联程度越高。
-
综合评价:将各个指标的关联度系数进行加权综合,得到最终的综合评价结果。权重的分配可以根据实际需求和决策者的主观判断来确定。
2.计算公式
计算灰色关联系数:
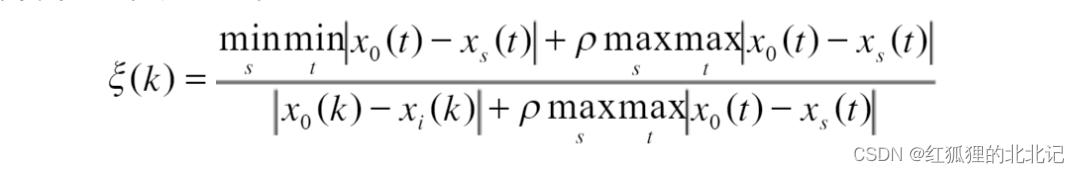
计算灰色加权关联度,计算公式为:
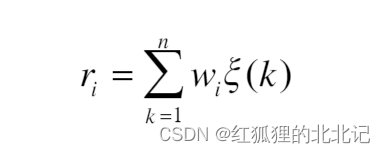
其中ri就是第i个指标对理想对象(参考数列,一般该数列都是1,就是最有情况)的加权关联度。就可以认为是评价的结果。
3.程序实例
通过对某健将级女子铅球运动员的跟踪调查,获得其 1982年至1986年每年最好成绩及16项专项素质和身体素质的时间序列资料,试对此铅球运动员的专项成绩进行因素分析。
import pandas as pd
import numpy as np
from factor_analyzer import FactorAnalyzer
# 创建数据框
data = pd.DataFrame({
'Year': [1982, 1983, 1984, 1985, 1986],
'Specialty_Score': [80, 85, 78, 90, 87],
'Quality1': [3.5, 4.2, 3.8, 4.0, 3.9],
'Quality2': [2.5, 2.8, 3.2, 2.9, 3.1],
'Quality3': [4.8, 4.5, 4.7, 4.9, 4.6],
'Physical1': [8, 8.5, 9, 8.2, 8.6],
'Physical2': [6.5, 6.7, 6.9, 7.2, 7.0],
'Physical3': [9.5, 9.2, 9.8, 9.4, 9.6]
})
# 提取因素分析所需的数据
factor_data = data.iloc[:, 2:]
# 创建因素分析对象
fa = FactorAnalyzer(n_factors=3, rotation='varimax')
# 执行因素分析
fa.fit(factor_data)
# 获取因子载荷矩阵
loadings = fa.loadings_
# 打印因子载荷矩阵
print("因子载荷矩阵:")
print(loadings)
在这个示例中,我们创建了一个包含专项成绩和素质的数据框。然后,我们使用FactorAnalyzer类创建了一个因素分析对象,并使用fit方法对数据进行因素分析。我们设置了3个因子,并选择了旋转方法为varimax。最后,我们获取并打印因子载荷矩阵,它显示了每个指标与每个因子之间的相关性。
4.运行结果
因子载荷矩阵:
[[ 0.19683026 -0.94019786 0.27004129]
[ 0.89526287 -0.06774054 0.44116648]
[-0.45872014 0.57584204 0.51864933]
[ 0.97239538 -0.09571545 0.00547983]
[ 0.26233715 -0.14818179 0.95437284]
[ 0.63675259 0.76214372 0.11820335]]