[该题的牛客链接](https://www.nowcoder.com/questionTerminal/8ee967e43c2c4ec193b040ea7fbb10b8?

---

一、方法一：%/达到二进制位右移的效果

//方法一
//         
//10 % 2 -> 0
//10 /= 2 -> 5 -> 101
// 
// 5 % 2 -> 1 -> count+1
// 5 /= 2 -> 2 -> 10
// 
// 2 % 2 -> 0
// 2 /= 2 -> 1 -> 1
// 
// 1 % 2 -> 1 -> count+1
// 1 /= 2-> 0 -> 跳出循环
//count得到就是2 
#include<stdio.h>

int Count(int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
		{
			count++;
		}
		n /= 2;
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Count(n);
	printf("%d\n", ret);
	return 0;
}

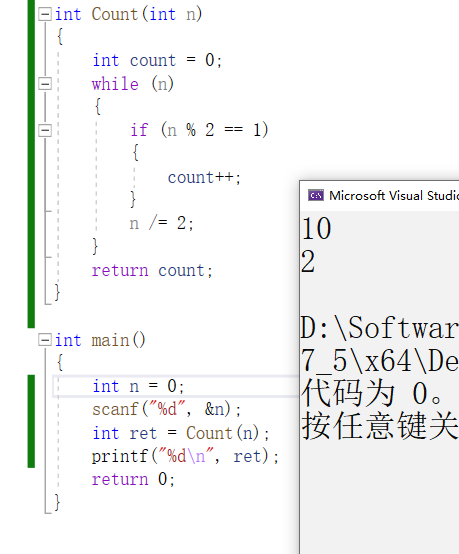
代码上方注释也给出了大概解释，这里我再用文字解释一下。
我们拿10举例，10的二进制是1010，共两个1
首先10%2得到结果为0，不做处理
然后再让10/=上2，得到结果为5，此时我们可以注意到，5的二进制是101
然后再让5%2，得到结果是1，此时让count加1
然后再让5/=2，得到结果为2，二的二进制是10
然后可以让2在%2得到结果为0，同样不做处理
然后2/=2得到结果为1，对应二进制就是1
然后1%2，结果是1，让count在加1
然后1/=2结果是0，最终跳出循环
我们可以发现，每次/=得到的二进制数从1010到101再到10最好到1，有种类似二进制数不断右移的效果，每次右移之后再判断末位是否为1就行，因此同样除了使用%/方法外，我们可以直接用>>来实现

1.1用>>操作符实现

//就是把/= 换成>>=，只是用/=更好理解一些
#include<stdio.h>

int Count(int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
		{
			count++;
		}
		n >>= 1;
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Count(n);
	printf("%d\n", ret);
	return 0;
}

1.2方法一代码的改进（针对负数情况）

回到最开始的代码，当我们输入负数时

会发现结果竟然是0，但是-1的补码是32个1呀，结果应该是32才对
那我们再来分析一下
-1 % 2 等于-1，count还是0
然后-1 /= 2等于 0，跳出循环，所以结果最终是0
改进代码：

#include<stdio.h>

int Count(unsigned int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
		{
			count++;
		}
		n /= 2;
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Count(n);
	printf("%d\n", ret);
	return 0;
}

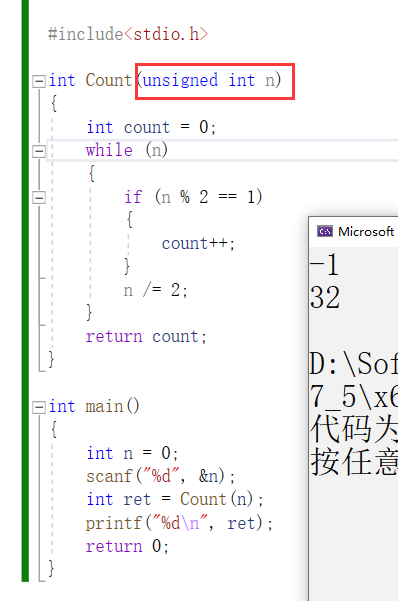
分析：当形参用int时，-1传进去就还是-1，因为看作有符号数，就把-1的补码再转回源码得到-1
而当用unsigned int时，-1的补码就被当作无符号数了，所以转成源码就还是32个1了，可以正常计算1的个数了
但是但是，牛客的题目是接口类型的，形参类型已经给定是int了，所以这个代码还是无法通过

二、方法二：按位与1（&1）来判断最末位是否是1

#include<stdio.h>

int Count(unsigned int n)
{
	int count = 0;
	for (int i = 0; i < 32; i++)
	{
		if (1 == ((n >> i) & 1))
		{
			count++;
		}
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Count(n);
	printf("%d\n", ret);
	return 0;
}

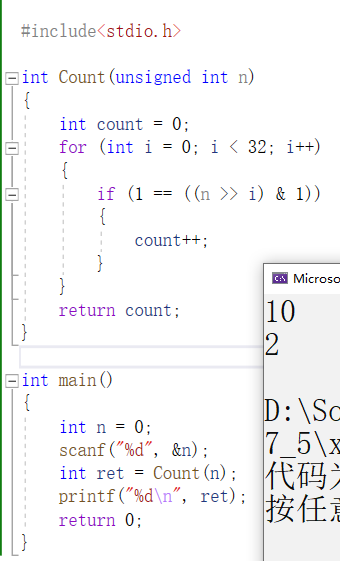
当然-1也是可以的

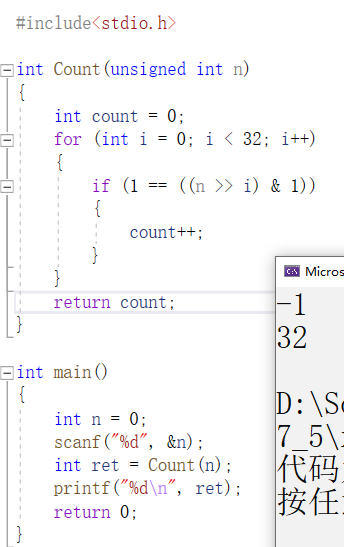
分析：

当一个数对应的二进制数补码末位为1时，该数&1结果为1，末位为0时结果为0
总结：一个数&1能得到该二进制的最末位，该数|0（或上0）也可以达到该效果。

三、方法三：n = n&(n-1)——比较难想到的方法

首先，我们看看方法二里面的不足：不管二进制数中有几个1，循环都要执行32次，严重影响效率
改进：n = n&(n-1)

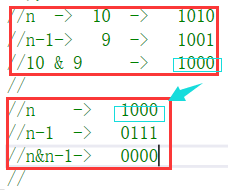
每个红框就是执行一次n = n&(n-1)，当最终执行结果为0时停止，执行几次就代表最开始的n的二进制中有几个1
原理：每次的减一操作，能够将二进制最靠右的1给减掉，因为这个1的右边全是0，减一需要借位了，刚好把1给借掉，可以导致n和n-1的1、0错位，再&之后就全是0了，这样一套操作就能消除一个零
这个方法就能避免方法二的缺点，当计算1对应二进制位1的个数时只会执行一次！

拓展——判断一个数是不是2的幂次方（非负整数）

常规解法不写，写一个通过方法三拓展出来的方法
这题的关键是找到2的幂次方数的特点：对应的二进制数中1的个数为1，例如1——1，2——10，4——100，8——1000…所以只要n&(n-1)的结果等于0，就代表者只要一个1！

#include<stdio.h>

int Power(int n)
{
	return !(n & (n - 1));
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	if (Power(n))
	{
		printf("%d是2的幂次方", n);
	}
	else
	{
		printf("%d不是2的幂次方", n);
	}
	return 0;
}