选择排序--简单选择排序，堆排序（大根堆，小根堆的建立，堆排序，插入删除元素）包含程序

news2024/11/27 10:24:27

 选择排序：每一趟从待排序列中选择最小的元素作为有序子序列中的元素，待元素只剩下一个，就不用选了。

一，简单选择排序

1.过程：假设以A[]表示数组

1.1最开始定义一个变量用来存储数组数组第一个元素的序号 i = 0; min = i，A[min] = 49;

数组序号01234567
待排序列4938659776132749

1.2用min对应数组中的元素依次往后作比较，A[min] = 49 > A[1] = 38,所以此时min = 1,A[min] =38

然后继续向后进行比较，A[min] = 38 < A[2] = 65;   A[min] = 38 < A[3] = 97;  A[min] = 38 < A[4]=76

A[min] = 38 > A[5] = 13,所以令 min = 5,A[min] = 13;  A[min] = 13 < A[6] = 27; A[min] = 13<A[7]=49

此时序号min就是数组中最小的元素，因此交换位置A[min]和A[i];

数组序号01234567
待排序列1338659776492749

2.代码展示

//简单选择排序
void SelectSort(Str &L)
{
	for(int i = 0; i < L.length-1; ++i)//一共进行n-1趟
	{
	  int min = i;//记录最小元素的位置
	  for(int j = i+1; j < L.length; ++j)//在A[i...n-1]中选择最小的元素
		  if(L.data[j] < L.data[min])
			  min = j;//更新最小元素的位置
	  if(min != i)
		  swap(L.data[min],L.data[i]);//在swap函数中交换元素位置，函数中元素共移动了3次
	}
}

3.结果：

4.分析

空间复杂度：仅使用了常数个辅助单元，空间复杂度为O(1)

时间复杂度：在简单选择排序过程中，元素移动的操作次数很少，不会超过3(n-1)（假如是n个元素的逆序，故n-1个都是需要移动，在swap函数中，每次交换元素位置的时候移动3次，故不会超过3(n-1)） ;元素之间的比较次数与序列的初始状态无关，始终是n(n-1)/2次（每次都是从待排序列的第一个元素开始往后进行比较n-1+....+1）,所以时间复杂度为O(n^{2})。

二，堆排序

堆的定义：n个关键字序列L[1...n]称为堆，当且仅当该序列满足：

（1）L(i) >= L(2i) 且L(i) >= L(2i+1)或（2）L(i) <= L(2i)且L(i) <= L(2i+1)。可以将堆视为一棵完全二叉树，满足条件（1）的堆称为大根堆；满足条件（2）的堆称为小根堆。

1.过程

1.1创建堆的过程(以大根堆为例)

数组序号012345678
待排序列4938659776132749

 从左到右，从上到下，图的编号是1，2，3，4，5；

创建大根堆的步骤：

1.第1张图是待排序列按照完全二叉树的形式进行排版。

2.从完全二叉树的最后一个非终端结点开始，依次向上，与其左右孩子结点的最大值进行比较。

3.因为97只有左孩子且其值为49 ，97>49，所以不进行交换；因为13<27，所以65与其右孩子的值17进行比较，65>27,所以不进行交换；因为97>76,所以38与其左孩子的值97进行比较，38<97,所以进行交换，交换后如第2张图； 因为97>65, 所以49与其左孩子的值97进行比较，49<97,交换后如第3张图。

4.然后按照第3步进行检查，因为值为38的结点只有左孩子，所以38与其左孩子值为49进行比较，38<49,所以进行交换，交换后如第4张图；因为49<76,所以49与其右孩子值为76进行比较，49<76,所以进行交换，如第5张图。如此完成该例子的大根堆创建，结果就是第5张图。

创建大根堆的代码展示：

//以大根堆的形式调整元素所在位置
void MaxHeadAdjust(Str &L, int k)
{//将元素k为根的子树进行调整
	L.data[0] = L.data[k];//最开始将根结点元素放在序号为0的位置
	for(int i = 2*k; i <= L.length; i*=2)//沿着较大的子结点向下筛选
	{
		if(i < L.length  && L.data[i] < L.data[i+1])//当i < 待排序列的长度的时候才会，关键字才会有右孩子；如果左孩子的值小于右孩子的值，那么关键字就和右孩子的值进行比较
			i++;//i++就表示右孩子的序号
		if(L.data[0] >= L.data[i])//如果关键字大于等于孩子结点的值，那么就不需要进行交换
			break;//直接结束程序，也不需要再次下坠
		else
		{
			L.data[k] = L.data[i];//如果小于，那么就将孩子的值赋值到双亲结点
			k = i;//那么随之而来就是将关键字的序号进行改变
		}
	}
	L.data[k] = L.data[0];//确定最后位置之后就将原本存储到0序号的元素的值赋值到最终位置
}

//创建大根堆
void BuildMaxHeap(Str &L)
{
	for(int i = L.length/2; i >= 1; --i)//从i = [n/2] -- 1,反复调整堆
		MaxHeadAdjust(L,i);
}

1.2堆排序的过程（以大根堆为例）

堆排序：每一趟将堆顶元素加入有序子序列（与创建堆后的待排序列的最后一个元素交换），并且将序列长度降低1，然后现在的待排序列再次调整成大根堆。（小元素不断”下坠“）。 

1.第一张图是创建堆的时候的完全二叉树，然后将堆顶元素与最后一个元素进行交换，输出堆顶元素，然后减少待排序列的长度。

2.因为76>63,所以将元素38"下坠"，和76交换位置；得到图3，后续是同样步骤得到图4.

堆排序代码展示：

//大根堆堆排序算法
void MaxHeapSort(Str &L)
{
  BuildMaxHeap(L);
  for(int i = L.length; i >= 1; --i)
  {
	  printf("%d ",L.data[1]);
	  swap(L.data[1],L.data[i]);
	  L.length--;
	  MaxHeadAdjust(L,1);
  }
  printf("\n");
}

2.插入元素

基本思想：将元素插入到待排序列的后面一个位置，对于大根堆，向上比较双亲结点，构成符合大根堆的样子

代码展示：

//大根堆堆排序插入
void InsertMaxHeap(Str &L, int v)
{
	int i = ++L.length;//插入元素则数组的有效长度增加1
	int j = i/2;//双亲结点
	L.data[L.length] = v;//将值赋值给数组中
	while(L.data[i] > L.data[j])//进行比较
	{
		swap(L.data[i],L.data[j]);//大于则交换位置
		i = j;//继续向上比较
		j = i/2;
	}
}

 

3.删除元素

基本思想：将删除的元素用数组最后一个元素进行代替，然后再构造成大根堆

//大根堆堆排序删除
void DeletMaxHeap(Str &L, int &w)
{
  int i;
  printf("请输入想要删除数组元素的序号：\n");
  scanf_s("%d",&i);
  w = L.data[i];
  swap(L.data[L.length],L.data[i]);
  L.length--;
  MaxHeadAdjust(L,i);

}

 

 4.小根堆（过程和大根堆类似，改变符号就好了，此处就展示代码）

4.1创建小根堆

//以小根堆的形式调整数组中的元素
void MinHeadAdjust(Str &L, int k)
{
	L.data[0] = L.data[k];
	for(int i = 2*k; i <= L.length; i*=2)
	{
		if(i < L.length  && L.data[i] > L.data[i+1])
			i++;
		if(L.data[0] <= L.data[i])
			break;
		else
		{
			L.data[k] = L.data[i];
			k = i;
		}
	}
	L.data[k] = L.data[0];
}

//创建小根堆
void BuildMinHeap(Str &L)
{
	for(int i = L.length/2; i >= 1; --i)
		MinHeadAdjust(L,i);
}

4.2堆排序

//小根堆堆排序
void MinHeapSort(Str &L)
{
  BuildMinHeap(L);
  for(int i = L.length; i >= 1; --i)
  {
	  printf("%d ",L.data[1]);
	  swap(L.data[1],L.data[i]);
	  L.length--;
	  MinHeadAdjust(L,1);
  }
  printf("\n");
}

4.3插入元素

//小根堆堆排序插入
void InsertMinHeap(Str &L, int v)
{
	int i = ++L.length;
	int j = i/2;
	L.data[L.length] = v;
	while(L.data[i] < L.data[j])
	{
		swap(L.data[i],L.data[j]);
		i = j;
		j = i/2;
	}
}

4.4删除元素

//小根堆堆排序删除
void DeletMinHeap(Str &L, int &w)
{
  int i;
  printf("请输入想要删除数组元素的序号：\n");
  scanf_s("%d",&i);
  w = L.data[i];
  swap(L.data[L.length],L.data[i]);
  L.length--;
  MinHeadAdjust(L,i);

}

结果：

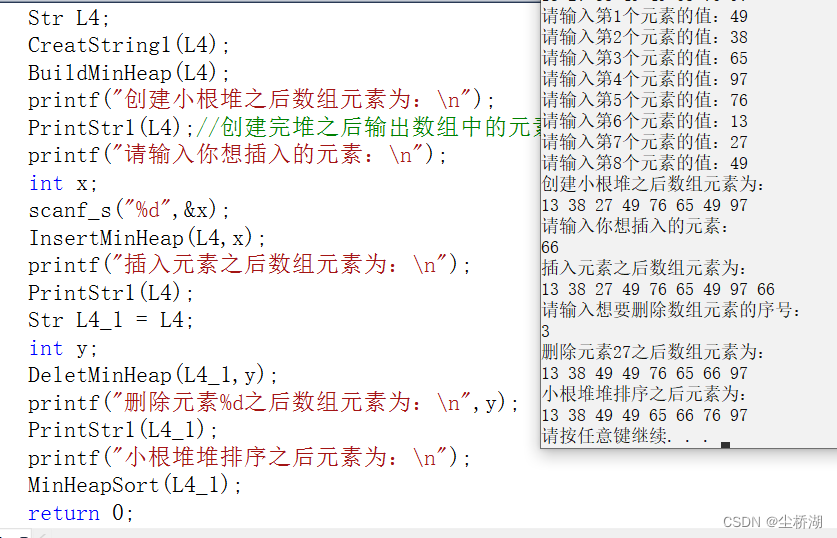
5.分析

在建含n个元素的堆时，关键字的比较次数不会超过4n，时间复杂度为O(n) 

空间复杂度：仅使用了常数个辅助单元1，所以空间复杂度为O(1)

时间复杂度：建堆时间为O(n),之后有n-1次向下调整，每次调整时间的复杂度为O(h),h = \log n为树高，故在最好最坏的平均条件下，堆排序的时间复杂度为O(n)+O(n\log n)  = O(n\log n) 

三，总结：

选择排序空间复杂度时间复杂度稳定性
简单选择排序O(1)O(n^{2})不稳定
堆排序O(1)O(n\log n) 不稳定

四，完整代码

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>

//定义数组结构体
typedef struct
{
  int *data;
  int length;
}Str;

//函数说明
void CreatString(Str &L);
void CreatString1(Str &L);
void swap(int &a, int &b);
void SelectSort(Str &L);
void PrintStr(Str L);
void PrintStr1(Str L);
//大根堆
void BuildMaxHeap(Str &L);
void MaxHeadAdjust(Str &L, int k);
void MaxHeapSort(Str &L);
void InsertMaxHeap(Str &L, int v);
void DeletMaxHeap(Str &L, int &w);

//小根堆
void BuildMinHeap(Str &L);
void MinHeapSort(Str &L);
void MinHeadAdjust(Str &L, int k);
void InsertMinHeap(Str &L, int v);
void DeletMinHeap(Str &L, int &w);

int main(void)
{
  Str L;
  CreatString(L);
  SelectSort(L);
  printf("简单选择排序之后数组元素为：\n");
  PrintStr(L);
  //大根堆
  Str L1;
  CreatString1(L1);
  printf("大根堆堆排序之后数组元素为：\n");
  MaxHeapSort(L1);//堆排序之后元素是有序的
  Str L2;
  CreatString1(L2);
  BuildMaxHeap(L2);
  printf("创建大根堆之后数组元素为：\n");
  PrintStr1(L2);//创建完堆之后输出数组中的元素，数组中元素不一定是有序的
  printf("请输入你想插入的元素：\n");
  int v;
  scanf_s("%d",&v);
  InsertMaxHeap(L2,v);
  printf("插入元素之后数组元素为：\n");
  PrintStr1(L2);
  Str L2_1 = L2;
  printf("堆排序之后数组元素为：\n");
  MaxHeapSort(L2);
  int w;
  DeletMaxHeap(L2_1,w);
  printf("删除元素%d之后数组元素为：\n",w);
  PrintStr1(L2_1);
  printf("删除元素之后堆排序为：\n");
  MaxHeapSort(L2_1);
  //小根堆
  Str L3;
  CreatString1(L3);
  printf("小根堆堆排序之后数组元素为：\n");
  MinHeapSort(L3);//堆排序之后元素是有序的
  Str L4;
  CreatString1(L4);
  BuildMinHeap(L4);
  printf("创建小根堆之后数组元素为：\n");
  PrintStr1(L4);//创建完堆之后输出数组中的元素，数组中元素不一定是有序的
  printf("请输入你想插入的元素：\n");
  int x;
  scanf_s("%d",&x);
  InsertMinHeap(L4,x);
  printf("插入元素之后数组元素为：\n");
  PrintStr1(L4);
  Str L4_1 = L4;
  int y;
  DeletMinHeap(L4_1,y);
  printf("删除元素%d之后数组元素为：\n",y);
  PrintStr1(L4_1);
  printf("小根堆堆排序之后元素为：\n");
  MinHeapSort(L4_1);
  return 0;
}


//创建数组
void CreatString(Str &L)
{
	L.data = (int *)malloc(sizeof(int)*8);
	L.length = 8;
	int val;
	for(int i = 0; i < L.length; ++i)
	{
	  printf("请输入第%d个元素的值：",i+1);
	  scanf_s("%d",&val);
	  L.data[i] = val;
	}
}

void CreatString1(Str &L)
{
 	L.data = (int *)malloc(sizeof(int)*12);
	L.length = 8;
	int val;
	for(int i = 1; i <= L.length; ++i)
	{
	  printf("请输入第%d个元素的值：",i);
	  scanf_s("%d",&val);
	  L.data[i] = val;
	} 
}

//简单选择排序
void SelectSort(Str &L)
{
	for(int i = 0; i < L.length-1; ++i)//一共进行n-1趟
	{
	  int min = i;//记录最小元素的位置
	  for(int j = i+1; j < L.length; ++j)//在A[i...n-1]中选择最小的元素
		  if(L.data[j] < L.data[min])
			  min = j;//更新最小元素的位置
	  if(min != i)
		  swap(L.data[min],L.data[i]);//在swap函数中交换元素位置，函数中元素共移动了3次
	}
}

//元素交换位置
void swap(int &a, int &b)
{
  int temp = a;
  a = b;
  b = temp;
}

//遍历输出
void PrintStr(Str L)
{
	for(int i = 0; i < L.length; ++i)
	{
		printf("%d ",L.data[i]);
	}
	printf("\n");
}

void PrintStr1(Str L)
{
	for(int i = 1; i <= L.length; ++i)
	{
		printf("%d ",L.data[i]);
	}
	printf("\n");
}



//以大根堆的形式调整元素所在位置
void MaxHeadAdjust(Str &L, int k)
{//将元素k为根的子树进行调整
	L.data[0] = L.data[k];//最开始将根结点元素放在序号为0的位置
	for(int i = 2*k; i <= L.length; i*=2)//沿着较大的子结点向下筛选
	{
		if(i < L.length  && L.data[i] < L.data[i+1])//当i < 待排序列的长度的时候才会，关键字才会有右孩子；如果左孩子的值小于右孩子的值，那么关键字就和右孩子的值进行比较
			i++;//i++就表示右孩子的序号
		if(L.data[0] >= L.data[i])//如果关键字大于等于孩子结点的值，那么就不需要进行交换
			break;//直接结束程序，也不需要再次下坠
		else
		{
			L.data[k] = L.data[i];//如果小于，那么就将孩子的值赋值到双亲结点
			k = i;//那么随之而来就是将关键字的序号进行改变
		}
	}
	L.data[k] = L.data[0];//确定最后位置之后就将原本存储到0序号的元素的值赋值到最终位置
}

//创建大根堆
void BuildMaxHeap(Str &L)
{
	for(int i = L.length/2; i >= 1; --i)//从i = [n/2] -- 1,反复调整堆
		MaxHeadAdjust(L,i);
}

//大根堆堆排序算法
void MaxHeapSort(Str &L)
{
  BuildMaxHeap(L);
  for(int i = L.length; i >= 1; --i)
  {
	  printf("%d ",L.data[1]);
	  swap(L.data[1],L.data[i]);
	  L.length--;
	  MaxHeadAdjust(L,1);
  }
  printf("\n");
}

//大根堆堆排序插入
void InsertMaxHeap(Str &L, int v)
{
	int i = ++L.length;//插入元素则数组的有效长度增加1
	int j = i/2;//双亲结点
	L.data[L.length] = v;//将值赋值给数组中
	while(L.data[i] > L.data[j])//进行比较
	{
		swap(L.data[i],L.data[j]);//大于则交换位置
		i = j;//继续向上比较
		j = i/2;
	}
}

//大根堆堆排序删除
void DeletMaxHeap(Str &L, int &w)
{
  int i;
  printf("请输入想要删除数组元素的序号：\n");
  scanf_s("%d",&i);
  w = L.data[i];
  swap(L.data[L.length],L.data[i]);
  L.length--;
  MaxHeadAdjust(L,i);

}



//以小根堆的形式调整数组中的元素
void MinHeadAdjust(Str &L, int k)
{
	L.data[0] = L.data[k];
	for(int i = 2*k; i <= L.length; i*=2)
	{
		if(i < L.length  && L.data[i] > L.data[i+1])
			i++;
		if(L.data[0] <= L.data[i])
			break;
		else
		{
			L.data[k] = L.data[i];
			k = i;
		}
	}
	L.data[k] = L.data[0];
}

//创建小根堆
void BuildMinHeap(Str &L)
{
	for(int i = L.length/2; i >= 1; --i)
		MinHeadAdjust(L,i);
}

//小根堆堆排序
void MinHeapSort(Str &L)
{
  BuildMinHeap(L);
  for(int i = L.length; i >= 1; --i)
  {
	  printf("%d ",L.data[1]);
	  swap(L.data[1],L.data[i]);
	  L.length--;
	  MinHeadAdjust(L,1);
  }
  printf("\n");
}


//小根堆堆排序插入
void InsertMinHeap(Str &L, int v)
{
	int i = ++L.length;
	int j = i/2;
	L.data[L.length] = v;
	while(L.data[i] < L.data[j])
	{
		swap(L.data[i],L.data[j]);
		i = j;
		j = i/2;
	}
}

//小根堆堆排序删除
void DeletMinHeap(Str &L, int &w)
{
  int i;
  printf("请输入想要删除数组元素的序号：\n");
  scanf_s("%d",&i);
  w = L.data[i];
  swap(L.data[L.length],L.data[i]);
  L.length--;
  MinHeadAdjust(L,i);

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/724213.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

赛效：怎么无损压缩Word文档

赛效：怎么无损压缩Word文档

1&#xff1a;在电脑上打开PDF猫&#xff0c;在导航栏的“文件压缩”菜单里点击“Word压缩”。 2&#xff1a;点击或者拖拽Word文档上传。 3&#xff1a;文件添加成功后&#xff0c;点击右下角“开始转换”。 4&#xff1a;转换成功后&#xff0c;文件下方有下载按钮&#xff0…
阅读更多...
快速搭建专属于自己的单商户商城系统！

快速搭建专属于自己的单商户商城系统！

<系统简介> 基于ThinkPHP6.0、Vue、uni-app、PHP8.0、MySQL5.7、element-ui等主流通用技术开发的一套likeshop单商户商城系统&#xff0c;真正做到好懂&#xff0c;易改&#xff0c;不绕弯 代码全开源 极易二开 可免费商用 系统适用于B2C、单商户、自营商城场景。完…
阅读更多...
SOLIDWORKS电控柜设计插件

SOLIDWORKS电控柜设计插件

电控柜设备的种类有很多种&#xff0c;但它们大体都是箱柜式的结构。电控柜是有标准的&#xff0c;但对于公司产品而言&#xff0c;针对不同的项目&#xff0c;如果都使用同一种规格的电控柜&#xff0c;又有可能空间太大&#xff0c;造成浪费&#xff0c;因此一般来说&#xf…
阅读更多...
Postman 连接/请求超时（远程服务/接口访问不上）

Postman 连接/请求超时（远程服务/接口访问不上）

一、问题情况 二、解决思路 接口访问不了&#xff0c;先看请求方式&#xff0c;然后看IP地址&#xff0c;发现都对着&#xff0c;但请求接口对应的端口号发现连接不上&#xff0c;于是想到是不是防火墙没有关&#xff08;不过理论上严谨一点&#xff0c;是只要把这个端口给开放…
阅读更多...
机器学习27：使用 Pandas 和 TensorFlow 进行数据建模编程实践

机器学习27：使用 Pandas 和 TensorFlow 进行数据建模编程实践

本文将详细介绍基于 Pandas 和 TensorFlow 探索、清理以及转换用于训练模型的数据集的方法&#xff0c;辅以代码和图片。 学习目标&#xff1a; 了解使用 Pandas 进行数据清理和处理丢失数据的基础知识。使用校准图评估模型性能。使用各种特征转换训练模型。使用可视化来了解…
阅读更多...
前端学习——jsDay5

前端学习——jsDay5

对象 对象使用 小练习 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"width…
阅读更多...
科技力量赋予 SK5 代理 HTTP 代理 IP 网络无限可能

科技力量赋予 SK5 代理 HTTP 代理 IP 网络无限可能

第一部分&#xff1a;智能网络加速技术 智能缓存&#xff1a;SK5 代理 HTTP 代理 IP 利用智能缓存技术&#xff0c;将经常访问的资源缓存在代理服务器中&#xff0c;从而实现更快速的资源加载和页面响应。这种智能化的缓存策略有效减少了对远程服务器的依赖&#xff0c;提升了用…
阅读更多...
产品经理学习画原型-登录界面

产品经理学习画原型-登录界面

开始画登录界面 选择一个矩形 常用修改&#xff1a; 选择文本标签&#xff1a; 设置字体、字号、颜色 添加水平线&#xff1a; 调整两个线连接&#xff0c;可以用CTRL加号、减号放大缩小画布来处理 选择一个主要按钮&#xff1a; 处理颜色、圆角 添加文本框&#xff1a; 设置高…
阅读更多...
Android性能分析【启动优化】

Android性能分析【启动优化】

作者&#xff1a;申国骏 性能分析工具 首先我们来学习一下如何使用性能分析的工具。我们从一个具体的例子出发&#xff0c;就是如何分析应用启动的性能。 Android Profiler 配置 我们来先看看Android Profiler。为了能在应用一启动就能马上捕捉到分析数据&#xff0c;我们需…
阅读更多...
python接口自动化（十八）--重定向（Location）（详解）

python接口自动化（十八）--重定向（Location）（详解）

简介 在实际工作中&#xff0c;有些接口请求完以后会重定向到别的url&#xff0c;而你却需要重定向前的url。URL主要是针对虚拟空间而言&#xff0c;因为不是自己独立管理的服务器&#xff0c;所以无法正常进行常规的操作。但是自己又不希望通过主域名的二级目录进行访问&#…
阅读更多...
Linux下make和makefile的使用方法

Linux下make和makefile的使用方法

1.make和makefile的区别 make是指令&#xff0c;makefile是文件&#xff0c;这是两者的却别。两者搭配使用&#xff0c;完成项目自动化创建。 2.make原理 make是如何工作的&#xff0c;也就是在默认情况下&#xff0c;我们只输入make命令&#xff0c;那么 1.make会在当前目录下…
阅读更多...
Python基础：函数和函数式编程

Python基础：函数和函数式编程

文章目录 函数和函数式编程函数函数式编程 函数和函数式编程 函数 声明函数&#xff1a; def hello():print("hello function!")调用函数&#xff1a; # 使用()调用 hello()#output:hello function!# 没有()&#xff0c;则不进行调用&#xff0c;一切皆是对象&am…
阅读更多...
Spring + Spring MVC + MyBatis+Bootstrap+Mysql酒店管理系统源码

Spring + Spring MVC + MyBatis+Bootstrap+Mysql酒店管理系统源码

IDEASpring Spring MVC MyBatisBootstrapMysql酒店管理系统源码 一、系统介绍1.环境配置 二、系统展示1. 管理员登录2.会员信息管理3.客房信息类型管理4.客房信息管理5.客房信息添加6.预定信息管理7.入住信息管理8.入住信息添加 三、部分代码UserMapper.javaUserController.j…
阅读更多...
MySQl数据库第四课-------------努力------努力------努力

MySQl数据库第四课-------------努力------努力------努力

作者前言 欢迎小可爱们前来借鉴我的gtiee秦老大大 (qin-laoda) - Gitee.com —————————————————————————————————— 目录 sudo whoami who exit reboot、shutdown 软件安装 编辑器vim ————————————————————————…
阅读更多...
9.2.2 【Linux】按键说明

9.2.2 【Linux】按键说明

第一部份&#xff1a;一般指令模式可用的按钮说明&#xff0c;光标移动、复制贴上、搜寻取代等 第二部份&#xff1a;一般指令模式切换到编辑模式的可用的按钮说明 第三部份&#xff1a;一般指令模式切换到命令行界面的可用按钮说明
阅读更多...
公网远程连接Redis数据库「内网穿透」

公网远程连接Redis数据库「内网穿透」

文章目录 1. Linux(centos8)安装redis数据库2. 配置redis数据库3. 内网穿透3.1 安装cpolar内网穿透3.2 创建隧道映射本地端口 4. 配置固定TCP端口地址4.1 保留一个固定tcp地址4.2 配置固定TCP地址4.3 使用固定的tcp地址连接 转载自cpolar极点云文章&#xff1a;公网远程连接Red…
阅读更多...
Python_列表比较大小

Python_列表比较大小

比较原理 从第一个元素顺序开始比较&#xff0c;如果相等&#xff0c;则继续&#xff0c;返回第一个不相等元素得比较结果。如果所有元素比较均相等&#xff0c;则长的列表大&#xff0c;一样长则两列表相等。 示例 a [5, 6, 3] b [5, 4, 3, 1] # 返回第1个不相等同位元素…
阅读更多...
计算机图形硬件（二） 5 - 3 图形工作站和观察系统、输入设备

计算机图形硬件（二） 5 - 3 图形工作站和观察系统、输入设备

1 图形工作站和观察系统 目前&#xff0c;大多数图形监视器以光栅扫描显示的方式工作&#xff0c;一般使用 CRT或平板系统。图形系统的范围从小型通用计算机系统到多监视器及超大幅面观察屏幕。个人计算机的屏幕分辨率从640x480到1280x1024屏幕对角线从12英寸到21英寸。多数通…
阅读更多...
基于STM32的300W无刷直流电机驱动方案

基于STM32的300W无刷直流电机驱动方案

如何驱动无刷电机&#xff1f; 近些年&#xff0c;由于无刷直流电机大规模的研发和技术的逐渐成熟&#xff0c;已逐步成为工业用电机的发展主流。围绕降低生产成本和提高运行效率&#xff0c;各大厂商也提供不同型号的电机以满足不同驱动系统的需求。现阶段已经在纺织、冶金、…
阅读更多...
【macOS 系列】下载brew或其他依赖包提示连接超时的问题解决

【macOS 系列】下载brew或其他依赖包提示连接超时的问题解决

在下载brew或其他依赖包提示连接超时 错误信息&#xff1a; curl: (7) Failed to connect to [raw.githubusercontent.com](http://raw.githubusercontent.com/) port 443 after 34 ms: Connection refused最简单的方式&#xff0c;就是修改DNS&#xff1a;为114.114.114.114…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023