文章目录
- LeetCode题号
- 104. 二叉树的最大深度
- 111. 二叉树的最小深度
- 144. 94. 二叉树的前序、中序遍历(DFS遍历)
- 589. 589. N 叉树的前、后序遍历
- 543. 二叉树的直径
- 102. 二叉树的层序遍历
LeetCode题号
- 简单 104. 二叉树的最大深度(DFS遍历法+分治)
- 简单 111. 二叉树的最小深度(BFS)
- 简单 144. 二叉树的前序遍历(DFS遍历)
- 简单 94. 二叉树的中序遍历(DFS遍历)
- 简单 589. N 叉树的前序遍历(DFS遍历)
- 简单 590. N 叉树的后序遍历(DFS遍历)
- 简单 543. 二叉树的直径(分治法)
- 中等 102. 二叉树的层序遍历(BFS)
104. 二叉树的最大深度

方法1:DFS
class Solution {
int maxDepth = 0;
int depth = 1;
public int maxDepth(TreeNode root) {
traverse(root);
System.out.println(depth);
return maxDepth;
}
public void traverse(TreeNode root){
depth++;
if(root == null) {
maxDepth = Math.max(maxDepth,depth);
System.out.println(depth);
return;
}
traverse(root.left);
traverse(root.right);
depth--;
}
}
方法2:分治:
- 首先,检查根节点是否为空。如果为空,说明该二叉树为空树,最大深度为 0。因此,返回 0。
- 如果根节点不为空,递归地计算左子树和右子树的最大深度,并取两者中的较大值。
- 最后,将较大值加上1,作为当前节点的深度,返回给上层递归调用。
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
111. 二叉树的最小深度
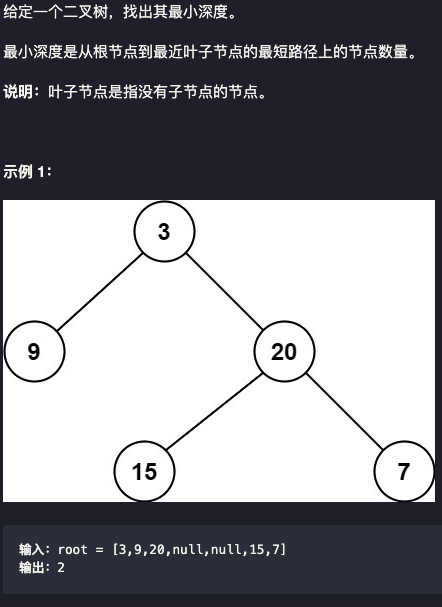
BFS方法:使用了广度优先搜索(BFS)来遍历二叉树的每个节点,并找到最小深度。通过使用队列来存储待处理的节点,并每次取出队列中的第一个节点进行处理,直到找到叶子节点为止。时间复杂度为 O(n),其中 n 是二叉树中的节点数量。
class Solution {
/**
* 函数 minDepth 接受一个二叉树的根节点 root 作为参数,并返回树的最小深度。
* @param root
* @return
*/
public int minDepth(TreeNode root) {
// 边界条件:根节点为空直接返回
if(root==null)return 0;
int deep = 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
deep++;
while (!queue.isEmpty()){
int qsize = queue.size();
for (int i = 0; i < qsize; i++) {// 遍历下一层的每个节点
TreeNode cur = queue.poll();
// 找到第一个叶子节点,其深度即为答案
if(cur.left==null&&cur.right==null){// 判断是否为叶子节点
return deep;
}
if(cur.left!=null){
queue.add(cur.left);
}
if(cur.right!=null){
queue.add(cur.right);
}
}
deep++; // 每一层的深度 + 1
}
return deep;
}
}
144. 94. 二叉树的前序、中序遍历(DFS遍历)
DFS前序遍历:
class Solution {
List<Integer> list = new ArrayList<>(); // 存储遍历结果
public List<Integer> preorderTraversal(TreeNode root) {
traverse(root);
return list;
}
void traverse(TreeNode root){
if(root == null)return;
list.add(root.val); // 二叉树的前序遍历位置
traverse(root.left);
traverse(root.right);
}
}
DFS中序遍历:
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> inorderTraversal(TreeNode root) {
traverse(root);
return list;
}
void traverse(TreeNode root){
if(root==null)return;
traverse(root.left);
list.add(root.val);// 二叉树的中序遍历位置
traverse(root.right);
}
}
589. 589. N 叉树的前、后序遍历
N叉树没有中序遍历,二叉树前中序遍历后都有。
DFS N叉树前序遍历:
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> preorder(Node root) {
DFS(root);
return list;
}
public void DFS(Node root){
if(root==null)return;
list.add(root.val); // 前序位置
for(Node n:root.children){ // 二叉树是左右两个子树、N叉树是n个子树
DFS(n);
}
}
}
DFS N叉树后序遍历:
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> postorder(Node root) {
DFS(root);
return list;
}
public void DFS(Node root){
if(root==null)return;
for(Node n:root.children){
DFS(n);
}
list.add(root.val); // 后序位置
}
}
543. 二叉树的直径

分治:计算每个节点的左右节点的深度之和,最大值即为答案。
class Solution {
int finalRes = 0;
public int diameterOfBinaryTree(TreeNode root) {
int r = maxDepth(root);
return finalRes;
}
int maxDepth(TreeNode root){
if(root ==null){
return 0;
}
int l = maxDepth(root.left); // 返回左节点的最大深度
int r = maxDepth(root.right);// 返回右节点的最大深度
// 后续遍历位置,计算当前左右节点最大深度之和
int oneRes = l+r;// 当前节点的左右节点深度之和(直径)
finalRes = Math.max(finalRes,oneRes); // 更新整棵树的最大直径
return Math.max(l,r)+1;// 返回当前节点的最大深度
}
}
102. 二叉树的层序遍历
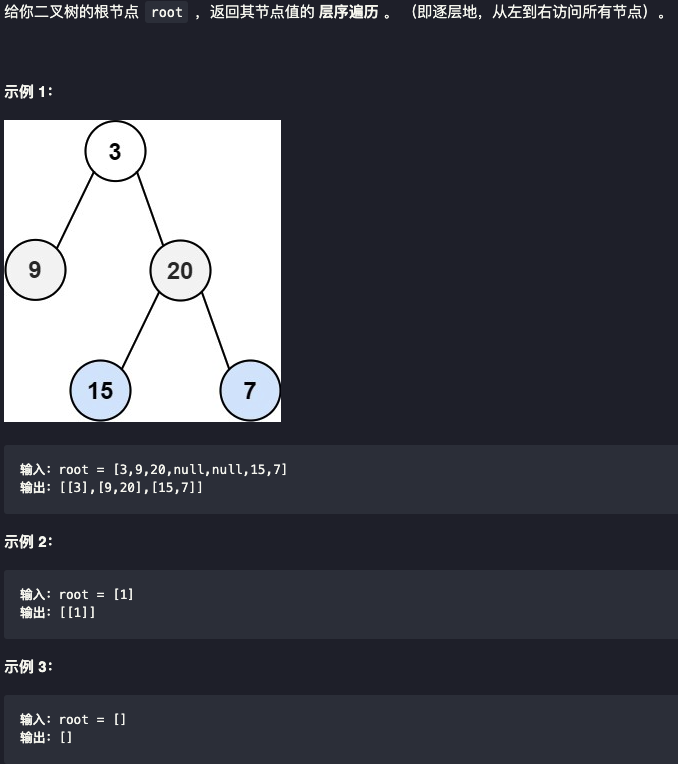
BFS:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> final_list = new ArrayList<List<Integer>>(); // 存放每一层的list
if(root == null){
return final_list;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
int queuesize = queue.size();
List<Integer> list = new ArrayList<Integer>();
for(int i =0; i < queuesize;i++){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
final_list.add(new ArrayList<Integer>(list));// 将每一层的结果放入最终结果中
}
return final_list;
}
}