算法与数据结构（六）

news2024/11/27 18:42:41

一、图

一、临接表

表示方法如下：
在这里插入图片描述
带权值的无向图的构建：

#define MaxInt 32767     // 极大值
#define MVNum 100        // 最大定点数
typedef int ArcType;     // 边的权值类型
typedef char VerTexType; // 顶点数据类型

//弧(边)的结点结构
struct ArcNode
{
    int adjvex;              // 该边指向顶点的下标
    struct ArcNode *nextarc; // 下一条边指针
    ArcType info;            // 边的权值
};

// 顶点的结点结构
typedef struct VNode
{
    VerTexType data;          // 顶点信息
    struct ArcNode *firstarc; // 指向第一条边关联该点的边
} VNode, AdjList[MVNum];

// 图的结构定义
typedef struct
{
    AdjList vertices;
    int vexnum, arcnum; // 图的顶点数和边数
} ALGraph;

创建图：

// 采用邻接表表示法创建无向网
Status CreateUDG(ALGraph &G)
{
    cin >> G.vexnum >> G.arcnum; // 输入总顶点数与总边数
    for (int i = 0; i < G.vexnum; ++i)
    {
        cin >> G.vertices[i].data;
        G.vertices[i].firstarc = NULL;
    }

    for (int k = 0; k < G.arcnum; ++k)
    {
        char v1, v2;
        cin >> v1 >> v2;
        int i = LocateVex(G, v1);
        int j = LocateVex(G, v2);

        ArcNode *p1 = new ArcNode;
        p1->adjvex = j;
        p1->nextarc = G.vertices[i].firstarc;
        G.vertices[i].firstarc = p1;

        ArcNode *p2 = new ArcNode;
        p2->adjvex = i;
        p2->nextarc = G.vertices[j].firstarc;
        G.vertices[j].firstarc = p2;
    }
    return 0;
}

//顶点在顶点表中的下标
int LocateVex(ALGraph G, VerTexType u)
{
    int i;
    for (int i = 0; i < G.vexnum; ++i)
       if (u == G.vertices[i].data) return i;
    return -1;
}

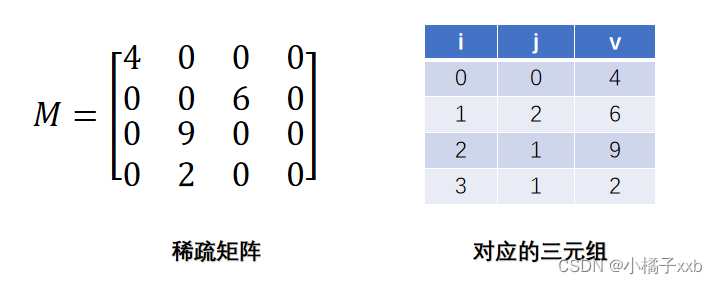
二、临接矩阵

表示如下：
在这里插入图片描述
带权值的有向图的构建：

#include <bits/stdc++.h>
using namespace std;
#define MaxVertices 100	//假设包含的最大结点数
#define MaxWeight -1	//假设两点不邻接的正无穷值

//定义结点
struct AdjMarix {
	int Vertices[MaxVertices];	//存储结点信息
	int Edge[MaxVertices][MaxVertices] = { 0 };	//存储每条边的权值
	int numV;	//当前顶点的个数
	int numE;	//当前边的个数
};

void CreatGraph(AdjMarix *G) {
	int vi, vj, w;
	cout << "请输入顶点数量：" << endl;
	cin >> G->numV;
	cout << "请输入顶点信息：" << endl;
	//输入结点的编号并初始化
	for (int i = 0; i < G->numV; i++) {
		cin >> vi;
		G->Vertices[i] = vi;
		G->Edge[i][i] = MaxWeight; //初始化过程先默认权值为无穷大
	}
	cout << "请输入边的数量：" << endl;
	cin >> G->numE;
	cout << "请输入边的信息：" << endl;
	for (int i = 0; i < G->numE; i++) {
		cin >> vi >> vj >> w; //vi、vj为邻接矩阵对应点的坐标，w为边的权值
		G->Edge[vi - 1][vj - 1] = w;
		//G->Edge[vj-1][vi-1]=w; 无向图需要再加上这一句
	}
}

//遍历图，展示邻接表矩阵
void ShowGraph(AdjMarix *G) {
	for (int i = 0; i < G->numV; i++) {
		for (int j = 0; j < G->numV; j++) {
			cout << G->Edge[i][j] << " ";
		}
		cout << endl;
	}
}

int main() {
	AdjMarix AM;
	CreatGraph(&AM);
	ShowGraph(&AM);
}

输入输出的结果为：
在这里插入图片描述

三、图的宽度优先遍历

1，利用队列实现
2，从源节点开始依次按照宽度进队列，然后弹出
3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
4，直到队列变空
邻接矩阵版：

#include <iostream>
#include <queue>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

// VertexType，顶点的数据类型
template<typename VertexType>
class MGraph {
private:
    VertexType Vex[MaxVertexNum];   //顶点表
    int Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexnum, arcnum;  //图的当前顶点数和弧数
    bool inq[MaxVertexNum]; //如果顶点i已入过,inq[i]==true。初值为false

    void BFS(int u) {   //遍历u所在的连通块
        queue<int> q;   //定义队列q
        q.push(u);   //初始顶点u入队
        inq[u] = true;  //设置u已入过队
        while (!q.empty()) {    //只要队列非空
            u = q.front();  //取出队首元素并访问
            cout << Vex[u] << "\t";
            q.pop();    //队首元素出队
            for (int v = 0; v < vexnum; v++)
                //如果u的邻接点v未曾加入过队列
                if (Edge[u][v] == 1 && inq[v] == false) {
                    //将v入队并标记已入队
                    q.push(v);
                    inq[v] = true;
                }
        }
    }

public:
    MGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            inq[i] = false;
            for (int k = 0; k < MaxVertexNum; k++)
                Edge[i][k] = 0;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> Vex[i];

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            Edge[row][col] = 1;
        }
    }

    void BFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++) //枚举所有顶点
            if (inq[u] == false)
                BFS(u); //遍历u所在的连通块
    }
};

int main() {
    MGraph<string> G;
    G.create();
    G.BFSTrave();
    return 0;
}

邻接表版：

#include <iostream>
#include <queue>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

struct ArcNode {    //边表结点
    int adjvex;     //该弧所指向的顶点的位置
    ArcNode *next;  //指向下一条弧的指针
};

template<typename VertexType>
struct VNode {        //顶点表结点
    VertexType data;  //顶点信息
    ArcNode *first;   //指向第一条依附该顶点的弧的指针
};

template<typename VertexType>
class ALGraph { //ALGraph是以邻接表存储的图类型
private:
    VNode<VertexType> vertices[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
    bool inq[MaxVertexNum]; //如果顶点i已入过,inq[i]==true。初值为false

    void BFS(int u) {   //遍历u所在的连通块
        queue<int> q;   //定义队列q
        q.push(u);   	//初始顶点u入队
        inq[u] = true;  //设置u已入过队
        while (!q.empty()) {
            u = q.front();  //取出队首元素并访问
            cout << vertices[u].data << "\t";
            q.pop();    //队首元素出队
            ArcNode *p = vertices[u].first;
            while (p) {
                if (inq[p->adjvex] == false) {
                    q.push(p->adjvex);
                    inq[p->adjvex] = true;
                }
                p = p->next;
            }
        }
    }

public:
    ALGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            inq[i] = false;
            vertices[i].first = NULL;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> vertices[i].data;

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            ArcNode *p = new ArcNode;
            p->adjvex = col;
            p->next = vertices[row].first;
            vertices[row].first = p;
        }
    }

    void BFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++) //枚举所有顶点
            if (inq[u] == false)
                BFS(u); //遍历u所在的连通块
    }
};

int main() {
    ALGraph<string> G;
    G.create();
    G.BFSTrave();
    return 0;
}

四、广度优先遍历

深度优先搜索以“深度”作为第一关键词，每次都是沿着路径到不能再前进时才退回到最近的岔道口。以一个有向图（见下图）进行 DFS 遍历来举例（从V0 开始进行遍历，黑色表示结点未访问，白色表示结点已访问，虚线边表示当前遍历路径）：
在这里插入图片描述

如果要遍历整个图，就需要对所有连通块（连通分量和强连通分量）分别进行遍历。所以 DFS 遍历图的基本思路就是将经过的顶点设置为已访问，在下次递归碰到这个顶点时就不再去处理，直到整个图的顶点都被标记为已访问。

#include <iostream>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

struct ArcNode {    //边表结点
    int adjvex;     //该弧所指向的顶点的位置
    ArcNode *next;  //指向下一条弧的指针
};

template<typename VertexType>
struct VNode {        //顶点表结点
    VertexType data;  //顶点信息
    ArcNode *first;   //指向第一条依附该顶点的弧的指针
};

template<typename VertexType>
class ALGraph { //ALGraph是以邻接表存储的图类型
private:
    VNode<VertexType> vertices[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
    bool visited[MaxVertexNum]; //如果顶点i已被访问,则visited[i]==true。初值为false

    void DFS(int u) {   //u为当前访问的顶点索引
        cout << vertices[u].data << "\t";
        visited[u] = true;   //设置u已被访问
        ArcNode *p = vertices[u].first;

        while (p) {
            if (visited[p->adjvex] == false)
                DFS(p->adjvex);
            p = p->next;
        }
    }

public:
    ALGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            visited[i] = false;
            vertices[i].first = NULL;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> vertices[i].data;

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            ArcNode *p = new ArcNode;
            p->adjvex = col;
            p->next = vertices[row].first;
            vertices[row].first = p;
        }
    }

    void DFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++)  //对每个顶点u
            if (visited[u] == false)  //如果u未被访问
                DFS(u); //访问u和u所在的连通块
    }
};

int main() {
    ALGraph<string> G;
    G.create();
    G.DFSTrave();
    return 0;
}

邻接矩阵版：

#include <iostream>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

// VertexType，顶点的数据类型
template<typename VertexType>
class MGraph {
private:
    VertexType Vex[MaxVertexNum];   //顶点表
    int Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexnum, arcnum;  //图的当前顶点数和弧数
    bool visited[MaxVertexNum]; //如果顶点i已被访问,则visited[i]==true。初值为false

    void DFS(int u) {   //u为当前访问的顶点索引
        cout << Vex[u] << "\t";
        visited[u] = true;   //设置u已被访问
        for (int i = 0; i < vexnum; i++)
            if (Edge[u][i] == 1 && visited[i] == false)
                DFS(i);
    }

public:
    MGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            visited[i] = false;
            for (int k = 0; k < MaxVertexNum; k++)
                Edge[i][k] = 0;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> Vex[i];

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            Edge[row][col] = 1;
        }
    }

    void DFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++)  //对每个顶点u
            if (visited[u] == false)  //如果u未被访问
                DFS(u); //访问u和u所在的连通块
    }
};

int main() {
    MGraph<string> G;
    G.create();
    G.DFSTrave();
    return 0;
}

二、拓扑排序

拓扑排序就是对一个有向无环图构造拓扑序列的过程：
1、在有向图中选一个没有前驱的顶点并输出。
2、从图中删除该顶点和所有以它为尾的弧。
代码如下：

#include <bits/stdc++.h>
using namespace std;
#define MAXVERTIES 20
#define OK 1
#define ERROR 0

int indegree[MAXVERTIES] = { 0 };	//用于存储入度信息

/*
5
1 2 3 4 5
6
1 2
1 4
1 3
2 4
3 5
4 5
*/

//定义结点
struct VexNode {
	int data;
	VexNode *next;
};

//定义弧
struct ArcNode {
	int data;
	VexNode *firstacr = NULL;
};

//定义邻接表
struct GraphList {
	ArcNode arclist[MAXVERTIES];
	int vexnum, arcnum;
};

//定义栈
struct Stack {
	int Sacklist[MAXVERTIES] = { 0 };
	int top = -1;
};

//入栈操作
void Push(Stack &S, int key) {
	if (S.top == MAXVERTIES) {
		cout << "栈已满！" << endl;
		return;
	}
	S.top++;
	S.Sacklist[S.top] = key;
}

//出栈操作
int Pop(Stack &S) {
	if (S.top == -1) {
		cout << "栈为空！" << endl;
		return -1;
	}
	int temp = S.Sacklist[S.top];
	S.top--;
	return temp;
}

//返回结点在结点数组中的下标
int Location(GraphList &G, int key) {
	for (int i = 0; i < G.vexnum; i++) {
		if (G.arclist[i].data == key) {
			return i;
		}
	}
	return -1;
}

//创建图
void CreatGraph(GraphList &G) {
	cout << "请输入顶点数：" << endl;
	cin >> G.vexnum;
	cout << "请输入顶点信息：" << endl;
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.arclist[i].data;
	}
	cout << "请输入弧数：" << endl;
	cin >> G.arcnum;
	cout << "请输入弧端点信息：" << endl;
	for (int i = 0; i < G.arcnum; i++) {
		int v1, v2;
		cin >> v1 >> v2;
		int Location1 = Location(G, v1);
		int Location2 = Location(G, v2);
		VexNode *new_node = new VexNode;
		new_node->data = Location2;
		new_node->next = G.arclist[Location1].firstacr;
		G.arclist[Location1].firstacr = new_node;
		indegree[Location2]++;
	}
}

//拓扑排序
int TopoSort(GraphList &G, int *topolist) {
	Stack S;
	int topo = 0;
	//先将所有入度为0的结点入栈
	for (int i = 0; i < G.vexnum; i++) {
		if (indegree[i] == 0) {
			Push(S, i);
		}
	}
	//依次出栈入度为0的结点
	while (S.top != -1) {
		int vx = Pop(S);
		topolist[topo++] = G.arclist[vx].data;	//输出结点
		VexNode *temp = G.arclist[vx].firstacr;
		//删除以该结点为尾的弧
		while (temp != NULL) {
			int index = temp->data;
			indegree[index]--;	//将该弧的弧头结点入度减1
			//如果入度为0，则入栈
			if (indegree[index] == 0) {
				Push(S, index);
			}
			temp = temp->next;
		}
	}
	topolist[topo] = -1;
	//如果拓扑序列中的元素个数等于所有元素个数，则该图无环，否则该图有环
	if (topo == G.vexnum) {
		return OK;
	} else {
		return ERROR;
	}
}

int main() {
	GraphList GL;
	CreatGraph(GL);
	int topolist[MAXVERTIES] = { 0 };
	int vx = TopoSort(GL, topolist);
	if (!vx) {
		cout << "有环！" << endl;
	} else {
		cout << "有向无环！" << endl;
		cout << "拓扑序列如下：" << endl;
		for (int i = 0; topolist[i] != -1; i++) {
			cout << topolist[i] << " ";
		}
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/724092.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

adb: failed to install .\xxxxxx.apk: Failure [INSTALL_FAILED_USER_RESTRICTED

adb: failed to install .\xxxxxx.apk: Failure [INSTALL_FAILED_USER_RESTRICTED

开发者模式和USB调试均已打开&#xff0c;adb安装时报错。看了一下&#xff0c;小米手机还需要开启USB安装才行。 问题已解决
阅读更多...
注册-Springboot整合邮件发送

注册-Springboot整合邮件发送

1.QQ邮箱开启服务 获取授权码 2.在配置文件进行相关配置 spring:mail:host: smtp.qq.comport: 587username: xxxpassword: xxxdefault-encoding: utf-8properties:mail:smtp:connectiontimeout: 5000timeout: 3000writetimeout: 5000 3.读取配置类 /*** 读取yml配置文件里面…
阅读更多...
乞丐版的四层负载均衡,你了解多少?

乞丐版的四层负载均衡,你了解多少?

大家好&#xff0c;我是蓝胖子&#xff0c;做开发的同学应该经常听到过负载均衡的概念&#xff0c;今天我们就来实现一个乞丐版的四层负载均衡&#xff0c;并用它对mysql进行负载均衡测试&#xff0c;通过本篇你可以了解到零拷贝的应用&#xff0c;四层负载均衡的本质以及实践。…
阅读更多...
深入解析Redis的LRU与LFU算法实现

深入解析Redis的LRU与LFU算法实现

作者&#xff1a;vivo 互联网服务器团队 - Luo Jianxin 重点介绍了Redis的LRU与LFU算法实现&#xff0c;并分析总结了两种算法的实现效果以及存在的问题。 一、前言 Redis是一款基于内存的高性能NoSQL数据库&#xff0c;数据都缓存在内存里&#xff0c; 这使得Redis可以每秒轻…
阅读更多...
矩阵的压缩存储

矩阵的压缩存储

本文主要内容&#xff1a;本文主要介绍几种特殊矩阵的压缩存储。特殊矩阵指具有许多相同矩阵元素或零元素&#xff0c;并且这些相同矩阵元素的分布有一定规律性的矩阵&#xff0c;常见的特殊矩阵有对称矩阵、上&#xff08;下&#xff09;三角矩阵、对角矩阵等。压缩存储指为多…
阅读更多...
Vite按需引入自定义组件unplugin-vue-components

Vite按需引入自定义组件unplugin-vue-components

1.安装插件 npm i unplugin-vue-components -D 2.vite.config.ts文件加如下代码 plugins: [vue({reactivityTransform: true}),Components({extensions: [vue, md],include: [/\.vue$/, /\.vue\?vue/, /\.md$/],dts: src/components.d.ts,deep: true, // 搜索子目录dirs: [s…
阅读更多...
MySQL体系结构及各结构的功能

MySQL体系结构及各结构的功能

MySQL体系结构 MySQL的体系结构实际就是MySQL数据库是由那些部分构成&#xff0c;每个部分的具体作用是什么。 Connectors&#xff1a; 用于不同的编程语言连接MySQL数据库&#xff0c;即对外提供的API。 Management Service &Utilities&#xff1a; 用于管理系统&…
阅读更多...
Android studio实现网上订餐app

Android studio实现网上订餐app

目录 一.应用分析 1.1应用总体描述 1.2应用开发环境 1.3应用模块说明 二.效果展示 2.1店铺界面 2.2店铺详情界面 2.3菜品详情界面 2.4订单界面 三.服务器数据准备 四.店铺功能业务实现 4.1搭建标题栏布局 1.创建项目 2.导入界面图片 3&#xff0e;搭建标题栏布局…
阅读更多...
旅游卡小程序分销系统开发

旅游卡小程序分销系统开发

旅游业的不断发展&#xff0c;旅游卡作为一种便捷的旅游方式越来越受到人们的青睐。为了吸引更多的游客&#xff0c;许多旅游卡品牌开始推出各种优惠活动&#xff0c;例如折扣、免费景点等。为了实现这些优惠活动&#xff0c;旅游卡品牌需要开发一款小程序分销系统&#xff0c;…
阅读更多...
主成分分析系列（一）概览及为什么数据要中心化

主成分分析系列（一）概览及为什么数据要中心化

一、概览 主成分分析&#xff08;Principle Component Analysis&#xff0c;PCA&#xff09;算法属于数据降维算法里面的一种。数据降维算法的主要想法是从高维度数据中找到一种结构&#xff0c;这种结构蕴含了数据中的大部分信息&#xff0c;从而将高维数据降维到低维数据&am…
阅读更多...
开利网络受邀参与广州三会数字化转型主题研讨会

开利网络受邀参与广州三会数字化转型主题研讨会

7月4日&#xff0c;开利网络受邀来到位于广州黄埔的视源集团总部&#xff0c;参与由广州三会组织的企业数字化转型主题系列研讨会。降本增效是企业经营的重要目标&#xff0c;本次数字化转型议题则从“会议”这一要素出发&#xff0c;探讨如何利用软硬件技术能力帮助企业完成会…
阅读更多...
《疯狂Android讲义》第2版 第3.5.2节关于Handler的代码

《疯狂Android讲义》第2版 第3.5.2节关于Handler的代码

类似定时切换商品效果&#xff1a; 布局文件&#xff1a; <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-…
阅读更多...
Python自动化测试面试题（精选版）

Python自动化测试面试题（精选版）

目录 项目相关 测试框架 测试工具 测试方法 Python基础 ​&#x1f381;更多干货 完整版文档下载方式&#xff1a; 今天由凡哥给你介绍一些Python自动化测试中常见的面试题&#xff0c;涵盖了Python基础、测试框架、测试工具、测试方法等方面的内容&#xff0c;希望能够…
阅读更多...
华为OD机试真题 Python 实现【优秀学员统计】【2023Q1 100分】，附详细解题思路

华为OD机试真题 Python 实现【优秀学员统计】【2023Q1 100分】，附详细解题思路

目录 一、题目描述二、输入描述三、输出描述四、补充说明五、解题思路六、Python算法源码七、效果展示1、输入2、输出3、说明 一、题目描述 公司某部门软件教导团正在组织新员工每日打卡学习活动&#xff0c;他们开展这项学习活动已经一个月了&#xff0c;所以想统计下这个月优…
阅读更多...
pdf转ppt怎么转换？分享这几个方法给大家！

pdf转ppt怎么转换？分享这几个方法给大家！

将PDF文件转换为PPT演示文稿是一项常见需求&#xff0c;无论是为了编辑、演示还是共享文件。 随着信息技术的不断进步&#xff0c;我们经常遇到需要将PDF文件转换为PPT演示文稿的情况。以下是四种简便的方法&#xff0c;供大家参考。 方法一&#xff1a;使用记灵在线工具 通…
阅读更多...
Salesforce Associate认证考试指南来啦！(内含备考攻略)

Salesforce Associate认证考试指南来啦！(内含备考攻略)

Salesforce Associate认证是一项全新的入门级认证&#xff0c;针对0-6个月Salesforce经验的学习者。这一新认证不再强调实践专业知识&#xff0c;而是验证并增强那些拥有Salesforce基础知识的备考者。这些知识包括了解CRM平台的用途、解决的业务需求&#xff0c;以及如何使用Sa…
阅读更多...
若依管理系统包名修改工具下载，使用教程（本人实测有效）

若依管理系统包名修改工具下载，使用教程（本人实测有效）

下载地址&#xff1a; 若依官网指定下载-Gitee包名修改文件下载地址 使用方法&#xff1a; 1.选择文件的地方需要选择zip压缩文件&#xff0c;把从若依官网拉下来的代码压缩成zip文件即可
阅读更多...
Django实现简单的音乐播放器 3

Django实现简单的音乐播放器 3

在原有音乐播放器上请求方式优化和增加加载本地音乐功能。 效果&#xff1a; 目录 播放列表优化 设置csrf_token 前端改为post请求 视图端增加post验证 加载歌曲 视图 设置路由 模板 加载layui css 加载layui js 增加功能列表 功能列表脚本实现 最终效果 总结 播…
阅读更多...
分布式监控之Zabbix6.0监控系统一

分布式监控之Zabbix6.0监控系统一

分布式监控之Zabbix6.0监控系统 前言一、Zabbix1、介绍2、zabbix监控原理3、Zabbix6.0版本新特性4、Zabbix6.0功能组件5、Zabbix与Prometheus对比 二、Zabbix6.0部署1、部署zabbix服务端2、添加 zabbix 客户端主机3、自定义监控内容4、zabbix 自动发现5、zabbix 自动注册 前言 …
阅读更多...
业务安全情报第十八期 | 知名手游开启公测，大批游戏账号遭抢注倒卖

业务安全情报第十八期 | 知名手游开启公测，大批游戏账号遭抢注倒卖

目录 某知名手游遭账号抢注倒卖 倒卖游戏者的风险特征 游戏运营商快速识别倒卖账号的黑灰产 网络游戏已经成为许多人娱乐和放松的重要途径。随着游戏玩家追求迅速提升角色等级和属性的愿望日益增长&#xff0c;游戏账号倒卖、账号出租越来越多&#xff0c;并逐步衍生出一条灰…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023