目录

84. 柱状图中最大的矩形

问题描述：

实现代码与解析：

单调栈

原理思路： 

---

84. 柱状图中最大的矩形

问题描述：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

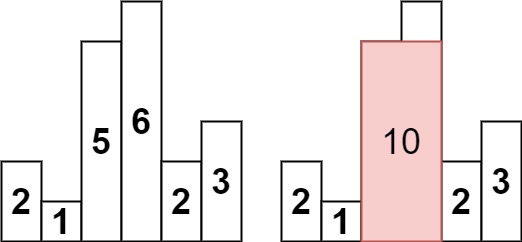
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

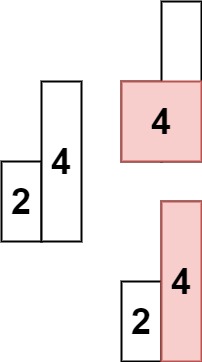
输入： heights = [2,4]
输出： 4

实现代码与解析：

单调栈

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        
        stack<int> stk;
        int res = 0;
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        stk.push(0);
        for (int i = 1; i < heights.size(); i++)
        {
            //栈里元素递增（从栈底到在栈顶）
            while (heights[i] < heights[stk.top()])
            {
                int mid = stk.top();
                stk.pop();
                int w = i - stk.top() - 1;
                int h = heights[mid];
                res = max(res, w * h);
            }
            stk.push(i);
        }

        return res;
    }
};

原理思路： 

        此题思想与Leetcode：42. 接雨水（单调栈C++）_Cosmoshhhyyy的博客-CSDN博客

相似，但是又有不同，可以先看看上面这题，对于本题思想更容易理解。

        还是单调栈的思路，但是这次我们栈的单调是从小到大（栈底到栈顶），我们要找的是第 i 个元素左侧的第一个比其大的值。把三个矩形看成一组来计算（这只是帮助理解的，其实消去多的话并不是三个，当然不算消去的就还是三个），根据我们的单调，此三个矩形就是：

左：栈顶元素的下面的元素      低

中：栈顶元素                           高

右：将要入栈的元素                低

        所以宽w = i - stk.top() - 1;高h = heights[mid];就可以求出此组的三个矩形所组成的最大矩形面具为 w * h 。

        这里可能会有人想为什么不是 w = i - stk.top(); h = heights[stk.top](栈中第二个的高)，运行可以对一部分测试样例。一开始我也理解错了，这里第一次求的是中间mid的矩形，因为每一个单个的矩形也算在其中。若图像为这样：

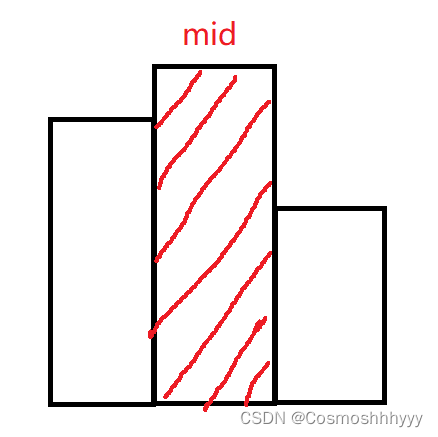
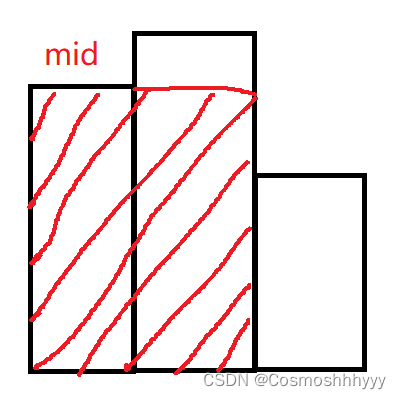
        第一次while其实算的是左侧的红色面积，第二次while才是算的右侧红色面积，第二次while中的mid变为第一次左侧的矩形。如果按照我们错误的思路是直接计算了右侧的图而忽略了左侧的情况。根据代码代入走一步就能真正的理解了。

        至于为什么栈和数组前面都加上0呢，因为是三个为一组嘛，将0加入，第二个元素肯定比0大，那么在循环到第三个元素时，就能确保是三个了。

        对于为什么数组后面加上0呢，因为我们写单调栈都会遇到最好栈里还有元素未弹出，我们把0入栈，就可以得到所有的结果并且栈里没有元素了。

        我们将每一个结果比较取一个最大值，这样就能得到最终结果啦。