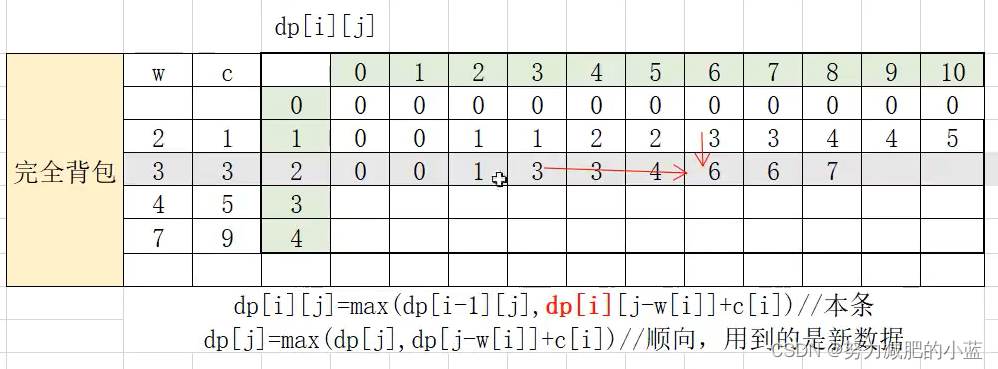
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
- 递推公式及顺序
01背包: dp[ i ][ j ] = max (dp[ i -1][ j - w[ i ] ] + v[ i ], dp[ i - 1 ][ j ])
完全背包:dp[ i ][ j ] = max (dp[ i ][ j - w[ i ] ] + v[ i ], dp[ i - 1 ][ j ])
区别:
01背包,不可以重复放入物品,所以在决定放入新物品时,需要用到 前 i-1种物品的数值,放到一维数组中,就是当前位置前面那个数字,也就是旧数据。所以需要逆序遍历才能保持前方旧数据保持不变
完全背包可以重复放,决定放入第 i 种物品时,这个物品在之前可能已经放进去了,需要用到的是 前 i 种物品的数值。 对应到一维数组,就是当前位置不断更新的值,也就是新数据,所以是正序
- for 循环嵌套的顺序-----无所谓
先背包,再物品, 物品每次都是从头遍历,实现了重复放
先物品,再背包, 背包容量变大,物品就可以放进去多个
完全背包解种类问题
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
518. 零钱兑换 II
题目:
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0。假设每一种面额的硬币有无限个。
分析:
(1) 可重复使用
(2)不强调顺序 2 2 1 == 1 2 2
(3)组合数 for循环遍历物品,内层for遍历背包。
同一个物品,先被反复的放, 再进行下一个物品,所以是没有顺序的组合数
- dp[ j ] 凑成总金额j的货币组合数为dp[j]
- 递推公式 dp[ j ] += d[ j - coins[ i ]]
dp[j],j 为5,已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。 - 初始化 dp[ 0 ] = 1;
- 递推顺序正序
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int>dp(amount+1, 0); // dp[i] 凑成金额i有多少种情况
dp[0] = 1;
for(int i=0; i<coins.size(); i++){
for(int j=1; j<=amount; j++){
if(j>=coins[i]){
dp[j] += dp[j-coins[i]];
}
}
}
return dp[amount];
}
};
377. 组合总和 Ⅳ
题目: 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
- 回溯
不同数字 —>不需要同层去重
可反复取用 —> 从当前开始
排列个数----> for循环从0开始 cur += dfs(candidates, target-candidates[i]);
防止超时----> 记忆化搜索---->剪枝
class Solution {
public:
unordered_map<int, int>mp;
int combinationSum4(vector<int>& nums, int target) {
sort(nums.begin(), nums.end());
int sum = dfs(nums, target);
return sum;
}
int dfs(vector<int>& candidates, int target){
if(mp.find(target)!=mp.end()){return mp[target];} //记忆化搜索
if(target == 0){
mp[target] = 1;
return 1;
}
int cur = 0;
for(int i=0; i<candidates.size(); i++){ // 可重复选用
if(target - candidates[i] < 0) break;
cur += dfs(candidates, target-candidates[i]); //问种类数
}
mp[target] = cur;
return mp[target];
}
};
- 完全背包
不同数字 —>不同物品
可反复取用 —> 完全背包
排列----> 外层for遍历背包,内层for循环遍历物品
同一个位置放入不同的物品, 下一个位置也允许放入之前放过的物品,那么之间是有顺序的 1 1 2 1 1 2 是排列数
注意: if(j>=nums[i] && dp[j] < INT_MAX - dp[j-nums[i]]) 防止两个数相加爆int
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int>dp(target+1, 0);
dp[0] = 1;
for(int j=0; j<=target; j++){
for(int i=0; i<nums.size(); i++){
if(j>=nums[i] && dp[j] < INT_MAX - dp[j-nums[i]] ){
dp[j] += dp[j-nums[i]];
}
}
}
return dp[target];
}
};