文章目录
- 一、题目
- 二、解法
- 2.1 暴力破解法
- 2.2 KMP算法
- 2.3 Sunday算法
- 2.4 官方查找算法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
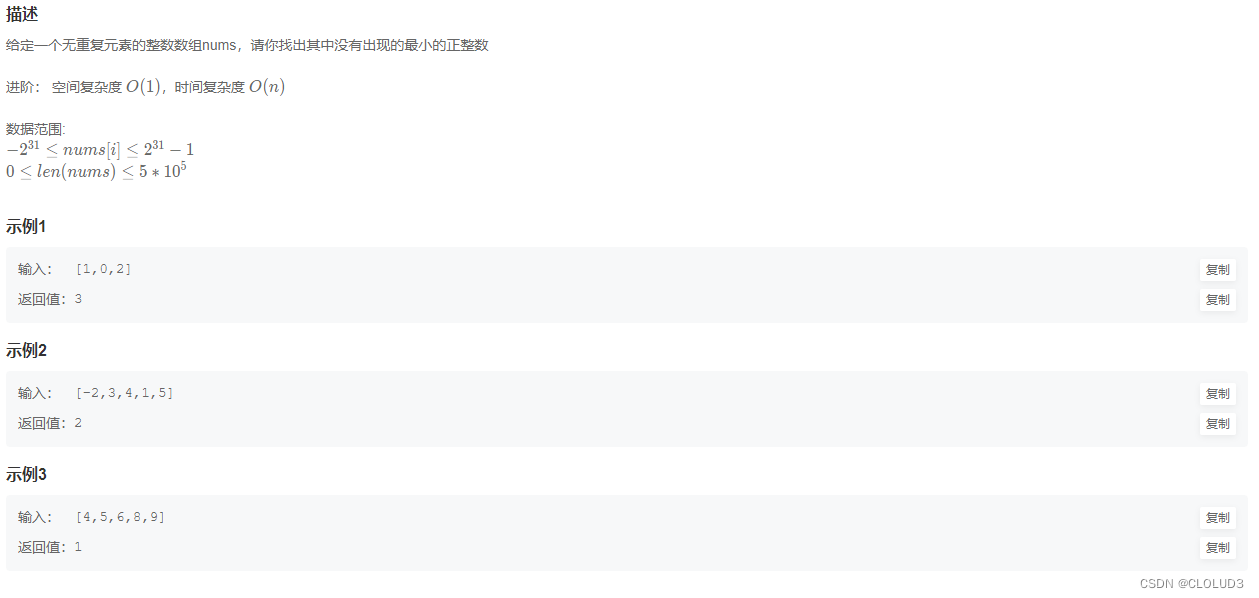
一、题目
二、解法
2.1 暴力破解法
思路分析:子串多次循环才能构成整个字符串,那么很容易想到使用一个for循环确定子串终止的位置,然后另一个for循环去遍历整个字符串。这道题在用暴力破解时也可以做简化,至少有两个子串,因此循环到 len/2 即可。
程序如下:
// 暴力破解法
bool repeatedSubstringPattern3(string s) {
int len = s.size();
for (int i = 0; i < len / 2; i++) { // 匹配到n/2
if (len % (i + 1)) continue; // 判断len是不是i+1的倍数,是倍数就进入循环
bool flag = true;
for (int j = i + 1; j < len; ++j) {
if (s[j] != s[j % (i + 1)]) {
flag = false;
break;
}
}
if (flag) return true;
}
return false;
}
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
2.2 KMP算法
思路分析:如果是重复子串构成的字符串,前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前后的子串做后串,就一定还能组成一个s。那么我们在 s+s 当中掐头去尾,在中间找到一个s那么说明这个字符串是一个循环子串构成的字符串。
程序如下:
// KMP算法实现
void getNext(int* next, string s) {
int j = -1;
next[0] = j;
for (int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if (s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern4(string s) {
if (!s.size()) return false;
int* next = new int[s.size()];
getNext(next, s);
int len = s.size();
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) return true;
return false;
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
2.3 Sunday算法
思路分析:思路和KMP算法相同,就是查找算法变成了Sunday算法,关于Sunday算法大家可以参考笔者这片文章【算法与数据结构】字符串匹配算法。
程序如下:
// Sunday算法
int Sunday(string haystack, string needle) {
if (haystack.size() < needle.size()) return -1; // 检查合法性
if (!needle.size()) return 0; // needle为空返回0
int shift_table[128] = { 0 }; // 128为ASCII码表长度
for (int i = 0; i < 128; i++) { // 偏移表默认值设置为 模式串长度 + 1
shift_table[i] = needle.size() + 1;
}
for (int i = 0; i < needle.size(); i++) { // 如果有重复字符也会覆盖,确保shift_table是 模式串最右端的字符到末尾的距离 + 1
shift_table[needle[i]] = needle.size() - i;
}
int s = 0; // 文本串初始位置
int j;
while (s <= haystack.size() - needle.size()) {
j = 0;
while (haystack[s + j] == needle[j]) {
++j;
if (j >= needle.size()) return s; // 匹配成功
}
// 找到主串中当前跟模式串匹配的最末字符的下一个字符
// 在模式串中出现最后的位置
// 所需要从(模式串末尾+1)移动到该位置的步数
s += shift_table[haystack[s + needle.size()]];
}
return -1;
}
bool repeatedSubstringPattern(string s) {
return Sunday((s + s).substr(1, 2 * s.size() - 2), s) != -1 ? true : false;
}
复杂度分析:
- 时间复杂度: 平均时间复杂度为 O ( n ) O(n) O(n),最坏情况时间复杂度为 O ( n ∗ m ) O(n*m) O(n∗m)。
- 空间复杂度: O ( 1 ) O(1) O(1),常量存储空间。
2.4 官方查找算法
// 使用官方查找算法
bool repeatedSubstringPattern2(string s) {
return (s + s).find(s, 1) != s.size();
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
三、完整代码
# include <iostream>
# include <string>
using namespace std;
class Solution {
public:
// Sunday算法
int Sunday(string haystack, string needle) {
if (haystack.size() < needle.size()) return -1; // 检查合法性
if (!needle.size()) return 0; // needle为空返回0
int shift_table[128] = { 0 }; // 128为ASCII码表长度
for (int i = 0; i < 128; i++) { // 偏移表默认值设置为 模式串长度 + 1
shift_table[i] = needle.size() + 1;
}
for (int i = 0; i < needle.size(); i++) { // 如果有重复字符也会覆盖,确保shift_table是 模式串最右端的字符到末尾的距离 + 1
shift_table[needle[i]] = needle.size() - i;
}
int s = 0; // 文本串初始位置
int j;
while (s <= haystack.size() - needle.size()) {
j = 0;
while (haystack[s + j] == needle[j]) {
++j;
if (j >= needle.size()) return s; // 匹配成功
}
// 找到主串中当前跟模式串匹配的最末字符的下一个字符
// 在模式串中出现最后的位置
// 所需要从(模式串末尾+1)移动到该位置的步数
s += shift_table[haystack[s + needle.size()]];
}
return -1;
}
bool repeatedSubstringPattern(string s) {
return Sunday((s + s).substr(1, 2 * s.size() - 2), s) != -1 ? true : false;
}
// 使用官方查找算法
bool repeatedSubstringPattern2(string s) {
return (s + s).find(s, 1) != s.size();
}
// 暴力破解法
bool repeatedSubstringPattern3(string s) {
int len = s.size();
for (int i = 0; i < len / 2; i++) { // 匹配到n/2
if (len % (i + 1)) continue; // 判断len是不是i+1的倍数,是倍数就进入循环
bool flag = true;
for (int j = i + 1; j < len; j++) {
if (s[j] != s[j % (i + 1)]) {
flag = false;
break;
}
}
if (flag) return true;
}
return false;
}
// KMP算法实现
void getNext(int* next, string s) {
int j = -1;
next[0] = j;
for (int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if (s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern4(string s) {
if (!s.size()) return false;
int* next = new int[s.size()];
getNext(next, s);
int len = s.size();
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) return true;
return false;
}
};
int main()
{
//string s = "abab";
//string s = "aba";
string s = "abcabcabcabc";
Solution s1;
bool result = s1.repeatedSubstringPattern3(s);
cout << "目标字符串" << s <<"是否由重复子串构成:" << endl;
if (!result) cout << "否" << endl;
else cout << "是" << endl;
system("pause");
return 0;
}
end


![[BitSail] Connector开发详解系列二:SourceSplitCoordinator](https://img-blog.csdnimg.cn/550ed4920d0042759355b66c8bfdb853.png)