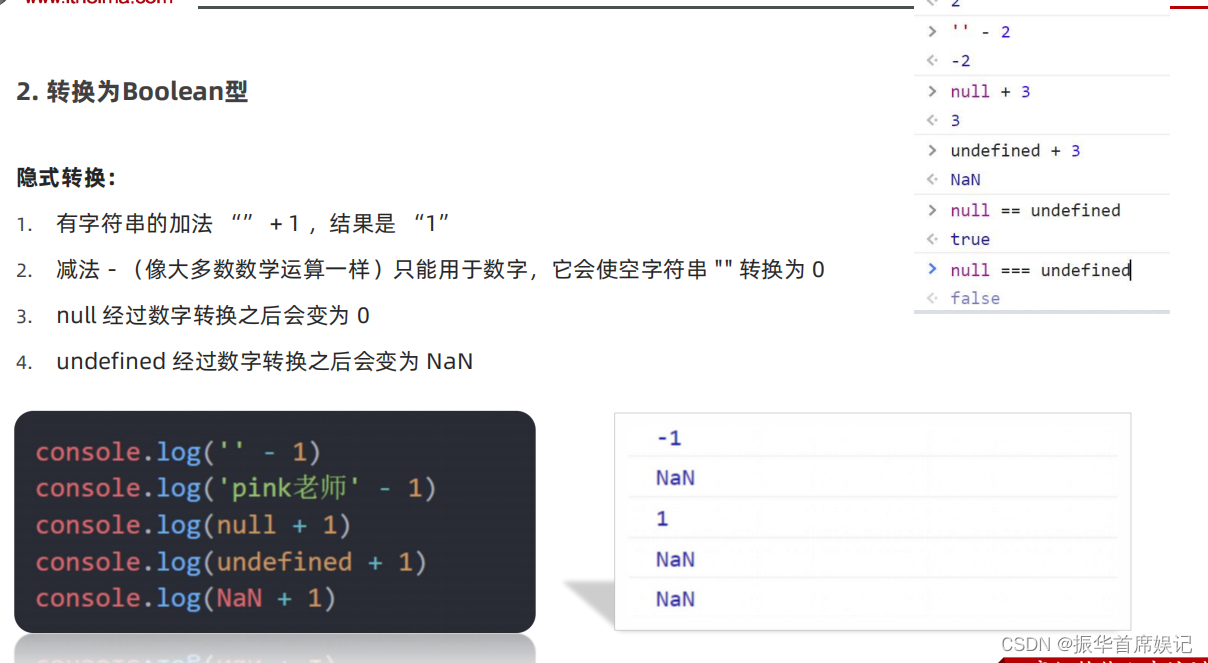
如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

看几个测试用例明白题意：

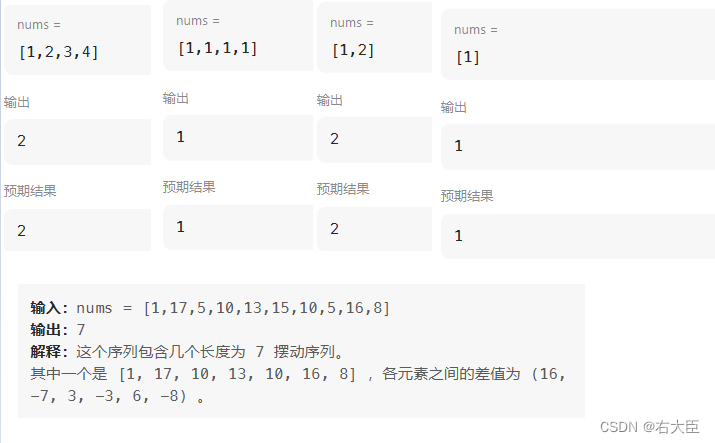
这个题可以用动态规划和贪心，我那天写的时候自己发现一个巨简单的思路，看了之前自己抄的题解和网上的题解，讲解的都很麻烦，各种坡度等等

这篇博客就记录下，我的写法

思路就是，用两个变量保存状态，当前状态和前一个状态，，当前差值大于0了，当前状态更新为1，小于0了状态更新为-1，不考虑等于0的情况，题也说了差值是0，不算摆动序列。每次循环结束都将当前状态保存为前一个状态，下一轮循环继续计算新状态。

什么时候更新结果呢？当当前状态不等于前一个状态时就更行，，也就是1不等于-1这种情况。。

那对于差值有0怎么办？前面判断了，差值时是0，状态不会改变，永远都是初始值，，那么只要一直是0，当前状态永远是初始值，，前状态也是初始值，我都初始化成0，那这样 更新结果的if他就永远进不去，，直到循环结束。范围结果就行，

 int wiggleMaxLength(vector<int>& nums) {

        // 记录状态，只有1 -1 0三种
        //差值大于0了，记录1
        //如果数组全是0或者差值是0怎么办？
        //这种情况记录状态的now永远不会改变，pre和now永远都是0
        //不会记录数字的
        //为啥ans要初始化成1？
        //因为我们从第二个数字和前一个的差值开始判断，默认只有一个元素，或者差值全是0的情况这些最后直接都返回ans为1 的结果，，也就不用特殊处理了
        //特殊情况可以写出来 对着代码看一遍就懂了
        int now=0;
        int pre=0;
        int ans=1;
        for(int i=0;i<nums.size();++i)
        {
            if(i>0)
            {
                int tmp=nums[i]-nums[i-1];
                if(tmp>0){
                    now=1;
                }
                else if(tmp<0){
                    now=-1;
                }
                if(now!=pre)
                {
                    ans++;
                }
                pre=now;    
            }
        }
 
        return ans;

    }