系列文章

【设计模式】七大设计原则
【设计模式】第一章：单例模式
【设计模式】第二章：工厂模式
【设计模式】第三章：建造者模式
【设计模式】第四章：原型模式
【设计模式】第五章：适配器模式
【设计模式】第六章：装饰器模式
【设计模式】第七章：代理模式
【设计模式】第八章：桥接模式
【设计模式】第九章：外观模式 / 门面模式
【设计模式】第十章：组合模式
【设计模式】第十一章：享元模式
【设计模式】第十二章：观察者模式
【设计模式】第十三章：模板方法模式
【设计模式】第十四章：策略模式
【设计模式】第十五章：责任链模式
【设计模式】第十六章：迭代器模式
【设计模式】第十七章：状态模式
【设计模式】第十八章：备忘录模式
【设计模式】第十九章：访问者模式

文章目录

系列文章
解释器模式
一、定义
二、角色分类
三、实现方式
- UML图
- 具体实现
四、应用场景
五、优缺点
- 优点
- 缺点

解释器模式

一、定义

**摘自百度百科：**定义了一个解释器，来解释给定语言和文法的句子。其实质是把语言中的每个符号定义成一个（对象）类，从而把每个程序转换成一个具体的对象树。

二、角色分类

抽象表达式/抽象解释器（Abstract Expression）

声明了一个所有具体表达式都要实现的抽象接口或抽象类，接口中存在一个解释操作的方法

终止符表达式（Terminal Expression）

实现与文法中的元素相关联的解释操作，通常一个解释器模式中只有一个终结符表达式，但有多个实例，对应不同的终结符

非终止符表达式（Nonterminal Expression）

文法中的每条规则对应于一个非终结符表达式，非终结符表达式一般是文法中的运算符或者其他关键字

上下文（Context）

该角色的任务一般是用来存放各个表达式所对应的值和定义的法则

客户角色（Client）

具体调用方法的角色

三、实现方式

UML图

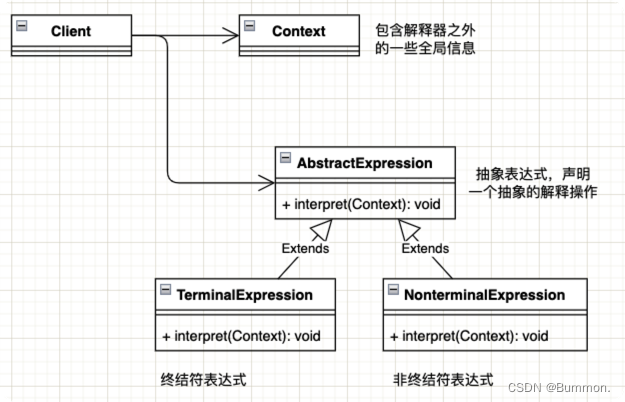
在这里插入图片描述

具体实现

接下来我们用解析数学表达式的示例来深入说明一下解释器模式

抽象解释器（Abstract Expression）

public interface AbstractExpression {
  /**
   * 解释操作
   */
  Object interpret();
}

终止符表达式（Terminal Expression）

public abstract class TerminalExpression implements AbstractExpression {
  protected AbstractExpression expressionA;
  protected AbstractExpression expressionB;

  public TerminalExpression(AbstractExpression expressionA, AbstractExpression expressionB) {
    this.expressionA = expressionA;
    this.expressionB = expressionB;
  }
}

非终止符表达式（Nonterminal Expression）

/**
 * 相加
 */
public class AddNonterminalExpression extends TerminalExpression {
  public AddNonterminalExpression(AbstractExpression expressionA, AbstractExpression expressionB) {
    super(expressionA, expressionB);
  }

  public int interpret() {
    return this.expressionA.interpret() + this.expressionB.interpret();
  }
}

/**
 * 相减
 */
public class SubNonterminalExpression extends TerminalExpression {
  public SubNonterminalExpression(AbstractExpression expressionBAbstractExpression expressionA, AbstractExpression expressionB) {
    return this.expressionA.interpret() - this.b.interpret();
  }
}

public class NumNonterminalExpression implements AbstractExpression {
  private int value;

  public NumNonterminalExpression(int value) {
    this.value = value;
  }
  
  public int interpret() {
    return this.value;
  }
}

上下文对象（Context）

public class Context {
  private Stack<AbstractExpression> stack = new Stack<AbstractExpression>();

  public Context(String expression) {
    this.parse(expression);
  }
  
  /**
   * 解析表达式
   */
  private void parse(String expression) {
    String[] elements = expression.split(" ");
    AbstractExpression expressionA, expressionB;

    for (int i = 0; i <elements..length; i++) {
      String operator = elements[i];
      if (Context.isOperator(operator)) {
        aExpr = this.stack.pop();
        System.out.println("出栈: " + aExpr.interpret());
        bExpr = new NumNonterminalExpression(Integer.valueOf(elements[++i]));
        TerminalExpression res = CalculatorContext.util(aExpr, bExpr, operator);
        this.stack.push(res);
        System.out.println("计算: " + aExpr.interpret() + operator + bExpr.interpret());
        System.out.println("计算结果: " + res.interpret() + " 入栈");
      } else {
        NumNonterminalExpression numNonterminalExpression = new NumNonterminalExpression(Integer.valueOf(elements[i]));
        this.stack.push(numNonterminalExpression);
        System.out.println("入栈: " + numNonterminalExpression.interpret());
      }
    }
  }

  /**
   * 计算结果
   */
  public int caculate() {
    int interpret = this.stack.pop().interpret();
    System.out.println("计算结果为：" + interpret + " 出栈");
    return interpret;
  }

  /**
   * 计算结果
   */
  public static TerminalExpression util(IExpression a, IExpression b, String symbol) {
    if (symbol.equals("+")) {
      return new AddNonterminalExpression(a, b);
     } else if (symbol.equals("-")) {
      return new SubNonterminalExpression(a, b);
     } else {
      return null;
    }
  }

  public static boolean isOperator(String symbol) {
    return (symbol.equals("+") || symbol.equals("-"));
  }
}

客户角色（Client）

public class Client {
  public static void main(String[] args) {
    // 创建上下文对象进行解释
    CalculatorContext calculatorContext = new CalculatorContext("1 + 4");
    // 获取执行结果
    System.out.println("calculatorContext.calculate() = " + calculatorContext.calculate());

    CalculatorContext calculatorContext2 = new CalculatorContext("1 + 4 - 5");
    System.out.println("calculatorContext.calculate() = " + calculatorContext2.calculate());
  }
}

运行结果

入栈: 1
出栈: 1
计算: 1+4
计算结果: 5 入栈
计算结果: 5 出栈
calculatorContext.calculate() = 5
入栈: 1
出栈: 1
计算: 1+4
计算结果: 5 入栈
出栈: 5
计算: 5-5
计算结果: 0 入栈
计算结果: 0 出栈
calculatorContext.calculate() = 0