1 现实问题

假设一个物体位于1000米处以自由落体运动，地面有一台具有特殊功能的雷达，对其进行观察，现需要对其下落的高度进行测量；
（1）建模
速度：V = gt
位置：Y = -Vt + Y0
（2）转化为状态空间方程
略

2 算法实现

import numpy as np
import matplotlib.pyplot as plt
"""
速度：V = g*t 
位置：Y = -V*t + Y0

"""
y0 = 1000.0
DT = 0.1
g = 9.8
SIM_TIME = 50.0  

GPS_NOISE = np.diag([1, 1]) ** 2
A = np.array([[1.0, 0.0],
             [-DT, 1.0]])

H = np.array([[1.0, 0.0],
              [0.0, 1.0]])

Q = np.diag([1.0, 1.0]) ** 2  
R = np.diag([1.0, 1.0]) ** 2  

def motion_model(x):
    #A = np.array([[1.0, 0.0],
    #              [-DT, 1.0]])
    x = A.dot(x)
    return x
   
def observation_model(x):
     #H = np.array([[1.0, 0.0],
     #             [0.0, 1.0]])
    
     z = H.dot(x)

     return z
    

def observation(xtrue):
    xTrue = motion_model(xtrue)
    z = motion_model(xTrue) + GPS_NOISE @ np.random.randn(2, 1)
    return xTrue,z
    
def kalman_filter(xEst, PEst, z):
    #  Predict 
    xPred =  motion_model(xEst)
    PPred = A @ PEst @ A.T
    #  Update
    zPred = observation_model(xPred)
    y = z - zPred
    S = H @ PPred @ H.T + R
    K = PPred @ H.T @ np.linalg.inv(S)
    xEst = xPred + K @ y
    
    PEst = (np.eye(len(xEst)) - K @ H) @ PPred
    return xEst, PEst
    
    
time=0



x_array = []    
y_array = []
z_array = []
k_array = []

xEst = np.zeros((2, 1))
PEst = np.eye(2)
xTrue = np.array([[g*DT],
              [y0]])
xEst[0]=g*DT 
xEst[1]=y0   
while SIM_TIME >= time:
    
    xTrue, z = observation(xTrue)
    xEst, PEst = kalman_filter(xEst, PEst,z)

    z_array.append(z[1])
    y_array.append(xTrue[1])
    k_array.append(xEst[1])
    x_array.append(time)
    time += DT
     
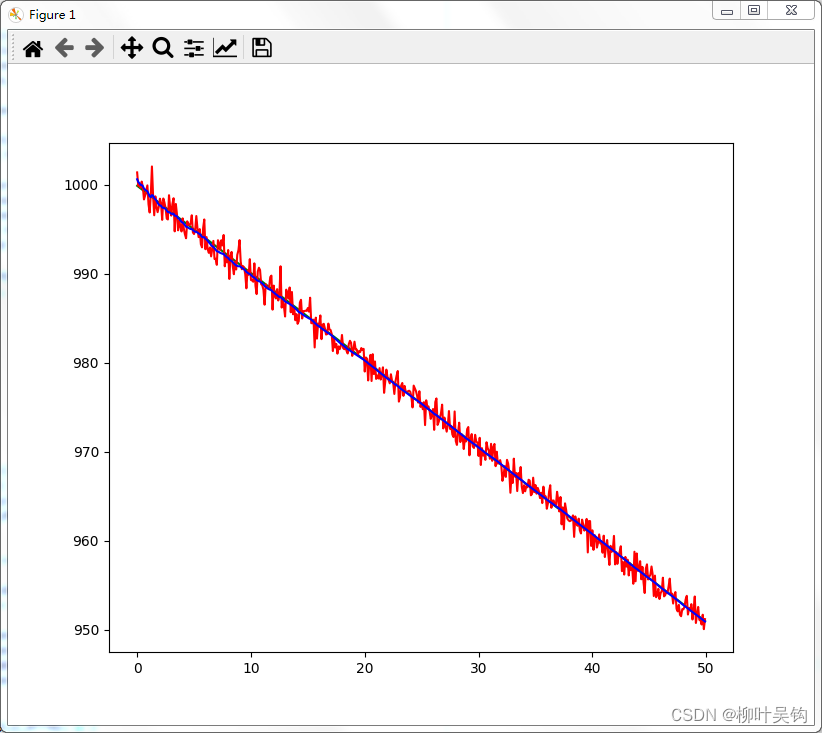
plt.plot(x_array,y_array,'g')
plt.plot(x_array,z_array,'r')
plt.plot(x_array,k_array,'b')
plt.show() 
 

3 实验结果