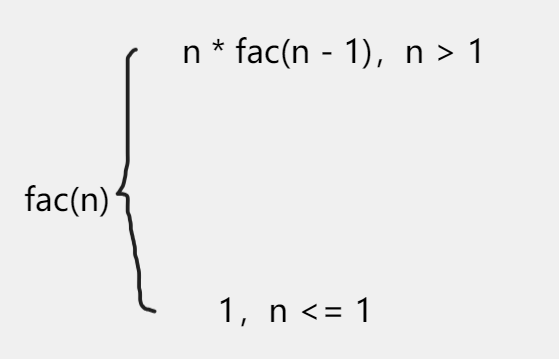文章目录
- 1. 打印一个整型的每一位
- 2. 求字符串长度
- 3. 求 n 的阶乘
- 4. 求第 n 个斐波那契数
- 4.1 递归算法
- 4.2 非递归算法
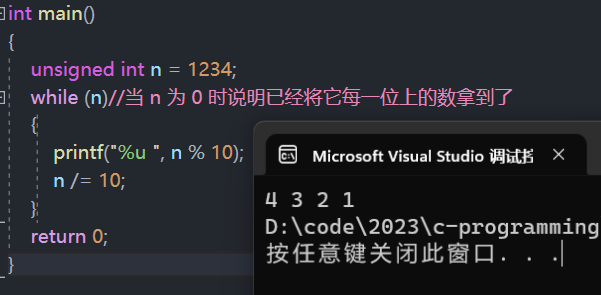
1. 打印一个整型的每一位
题目内容
- 接受一个整型值(无符号),按照顺序打印它的每一位。
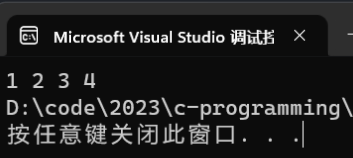
- 例如:输入 1234,输出 1 2 3 4。
如何得到 1234 的每一位?
- 如果想得到 1234 的最后一位的话,只需要 1234 %10 就可以得到 4,得到 4 之后将之打印出来;
- 既然已经得到了 4,那么就不在需要它了,此时用 1234 / 10 = 123 就能去掉最后一位数;
- 重复上面两个步骤,直到 1234 只剩个位数的时候停止循环即可。
- 此时已经了解了如何获取一个多位数上的每位数字,但是这个结果显然不是我们想要的正序打印,此时就该了解如何使用递归来求解了。
递归实现的解题思路
- 通过前面我们已经知道 1234 最好拿到的是最后一位的 4,然而我们想要正序打印就必须先拿到第一位的 1,然后将之打印出来。
- 也就是说,我们应该通过递归不停地 n / 10,直到 n 只剩第一位的 1 时结束递进开始回归。回归的过程中就可以很好的将 1234 的每一位打印出来了。
代码实现
#include <stdio.h>
void print(unsigned int n)
{
if (n > 9)// n>9 说明 n 还有的拆
{
print(n / 10);
}
printf("%u ", n % 10);//递推结束开始回归时这条语句才能被执行
}
int main()
{
unsigned int num = 1234;
print(num);
return 0;
}
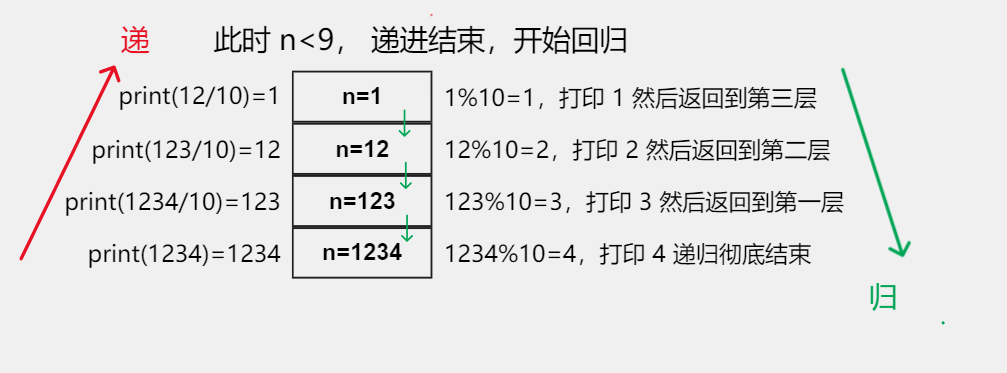
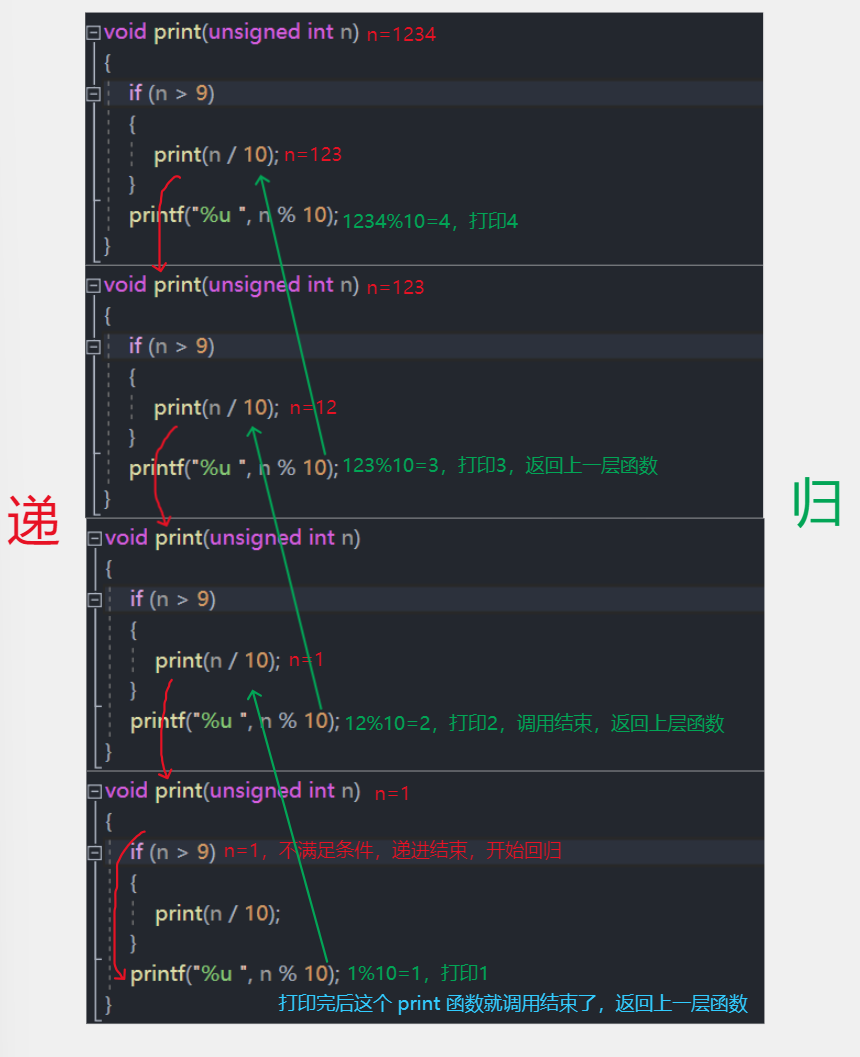
代码分析
看到递归了吗
2. 求字符串长度
题目内容
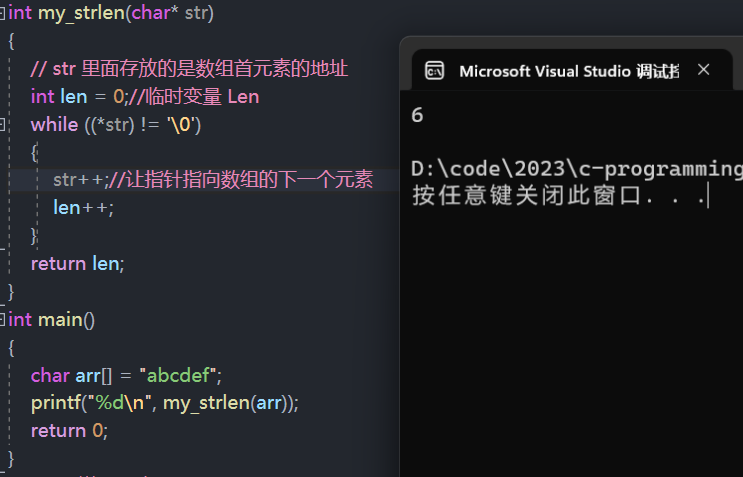
- 编写函数不允许创建临时变量,求字符串的长度。
- 一般而言,像这种求字符串长度的题,创建临时变量来做的话都蛮简单的。
- 但是不允许创建临时变量就显得很变态了,此时只能使用递归来写了。
解题思路
- 数组在传参的时候传过去的是数组首元素的地址,如果这个地址指向的第一个字符不是 \0 那串的长度就至少为 1,就可以进行递归;
- 每次递归让地址 +1 指向下一个字符,并且数量 +1 ,直到遇到 \0 递归结束,开始返回。
- 在回归过程中将遇到的所有 1 全部加起来就是串的长度。
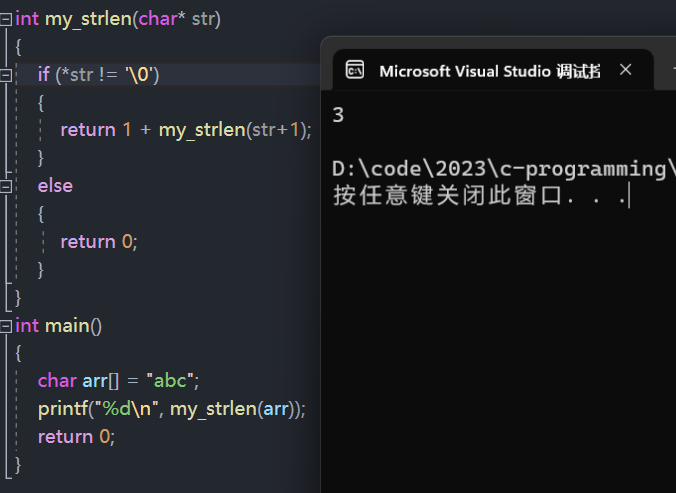
代码实现
#include <stdio.h>
int my_strlen(char* str)
{
//如果第一个字符不等于 \0,那它的长度至少是1
if (*str != '\0')
{
return 1 + my_strlen(str+1);
}
else
{
return 0;
}
}
int main()
{
char arr[] = "abc";
printf("%d\n", my_strlen(arr));
return 0;
}
代码分析
my_strlen(“abc”)
1 + my_strlen(“bc”)
1+1+my_strlen(“c”)
1+1+1+my_strlen(“”)
图解1
3. 求 n 的阶乘
阶乘公式
- 有了公式的话就很好解决了,递归套用公式就行了。
代码实现
#include <stdio.h>
int fac(int n)
{
if (n > 1)
{
return n * fac(n - 1);
}
else
{
return 1;// 0 和 1 的阶乘都是 1
}
}
int main()
{
int n;
scanf("%d", &n);//以 n = 5 做例子
printf("%d\n", fac(n));
return 0;
}
代码分析
4. 求第 n 个斐波那契数
斐波那契数
- 斐波那契数列指的是这样一个数列:
- 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711……
- 它们的规律是:这个数列从第 3 项开始,每一项都等于前两项之和。
4.1 递归算法
斐波那契数公式
- 通过求阶乘那节可以发现,在有了函数公式的情况下,递归写起来基本就是有手就行了;
- 斐波那契数当然也有自己的公式:
代码实现
#include <stdio.h>
int Fib(int n)
{
if (n > 2) //从第三位才开始求斐波那契数
{
return Fib(n - 1) + Fib(n - 2);
//公式:fib(n) = fib(n-1) + fib(n-2)
}
else
{
return 1; // 前两个斐波那契数都是 1
}
}
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", Fib(n));
return 0;
}
- 在使用 fib 这个函数的时候如果我们要计算第 50 个斐波那契数字的时候特别耗费时间。
- 博主的电脑在求第 50 个斐波那契数的时候用了有足足两分钟。
不推荐使用递归求斐波那契数
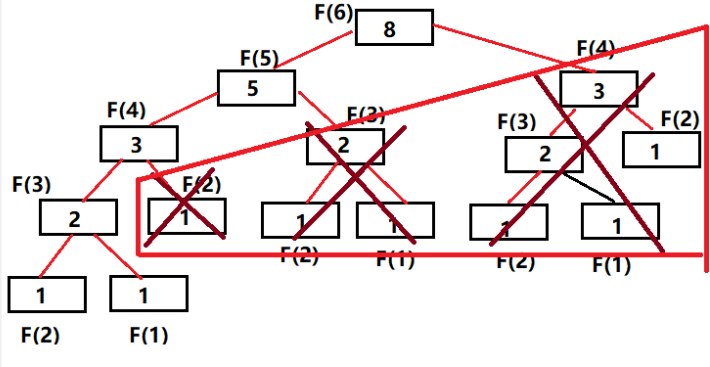
- 在使用递归求解斐波那契数的时候,会出现大量重复性的计算,导致程序执行效率很底。
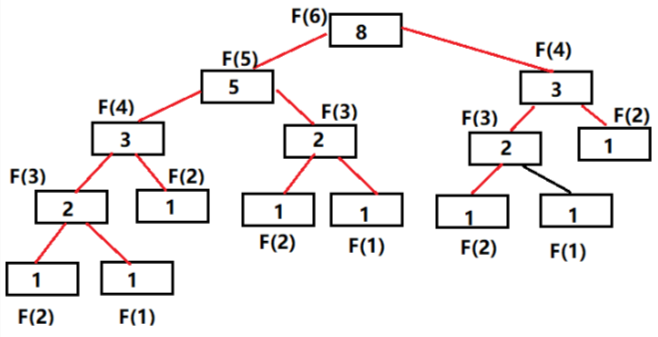
- 如下图:想求第 6 个斐波那契数就得先求出第 5 个以及第 4 个斐波那契数;
- 想求出第 5 个斐波那契数就又要先求 第 4 个以及第 3 个斐波那契数,这才第二步就开始出现重复运算了。
- 来看看在求第 40 个斐波那契数的过程中,重复求了第 3 个斐波那契数多少次:
#include <stdio.h>
int count_fib_3 = 0;
int Fib(int n)
{
//记录在运算某个数的过程中求了多少次第 3 个斐波那契数
if(3==n)
{
count_fib_3++;
}
if (n > 2)
{
return Fib(n - 1) + Fib(n - 2);
}
else
{
return 1;
}
}
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", Fib(n));
printf("%d\n", count_fib_3);
return 0;
}
可以看到,光是第 3 个斐波那契数就重复求了将近四千万次,那是相当的夸张。
4.2 非递归算法
- 为了解决用递归求斐波那契数出现的大量的重复计算现象,使用迭代求斐波那契数无疑是一个更好的选择。
迭代定义
- 迭代就是重复的意思;
- 循环是迭代,迭代不一定是循环。
解题思路
- 使用递归我们是从后往前算的,那么使用迭代我们就从前往后算。
- 使用三个变量来存储 第 1、2 个数以及前两数之和。
- 通过不断交换三个变量的值,从而在一条斐波那契数列上进行移动。
解题步骤
- 先将变量 a 和 b 的值都赋成 1,然后执行 a + b = c ;
- 从第 3 个数开始才去求斐波那契数,因为前两个斐波那契数都是 1。
- 算好之后将 b 的值赋给 a,将 c 的值赋给 b,然后执行 a + b = c,产生新的变量 a b c,然后将 n 的值减 1;
- 重复上面两个步骤,直到 n 的值等于 3 结束循环。
代码实现
#include <stdio.h>
int Fib(int n)
{
int a = 1, b = 1, c = 1;
while(n >= 3)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", Fib(n));
return 0;
}
- 现在算第 50 个斐波那契数虽然结果是错的,但是效率提升上来了。
- 使用了迭代的方法计算斐波那契数之后,需要重复计算的步骤就彻底被干掉了。