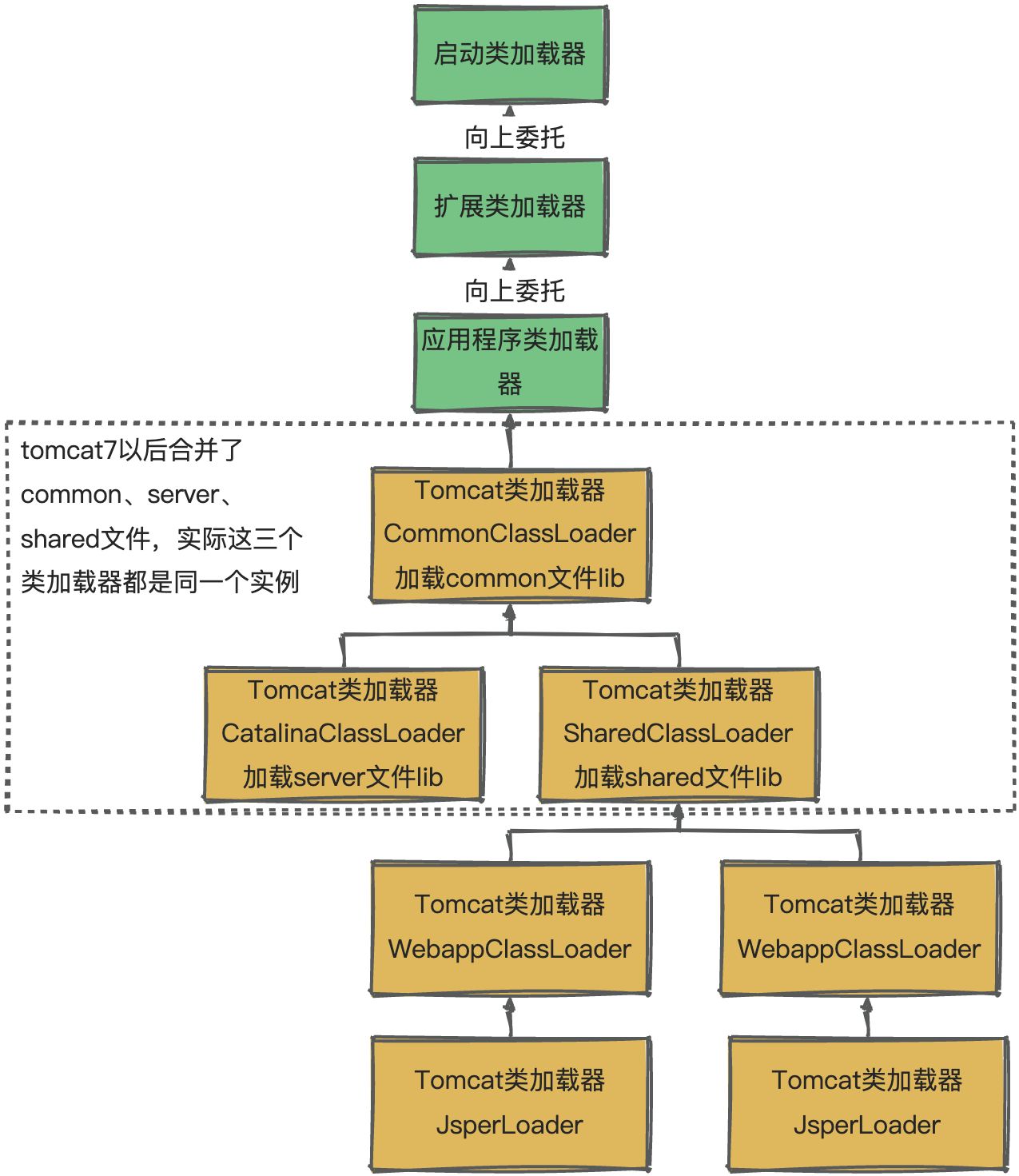
注意:我们统一用邻接矩阵和邻接表来存储树和图
int h[N], e[N], ne[N], w[N], idx;
int g[N][N];
void add(int a, int b, int c) //a->b 边权为c
{
e[idx] = b;
w[idx] = c
ne[idx] = h[a];
h[a] = idx ++;
}
void add(int a,int b, int c)
{
g[a][b] = c;
}0x21树和图的遍历
树与图的dfs遍历,dfs序,深度和重心
dfs遍历树与图
void dfs(int x)
{
vis[x] = true;
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
dfs(y);
}
}时间复杂度为边数加节点数M+N
时间戳
即每个节点被访问的顺序,我们只需要记录每一个节点被打上“已访问”时的cnt即可代码如下
int cnt[N], t = 1;
void dfs(int x)
{
cnt[x] = t ++;
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(cnt[y]) continue;
dfs(y);
}
}树的DFS序
我们在对树进行dfs时,对于每个节点,刚进入递归和即将回溯前记录一次该点的编号,最终得到的长度为2N的节点序列就称为DFS序,记每个节点编号为x在序列中出现的位置分别为L[x]和R[x]那么在[L[x],R[x]]内就是以x为根的子数的DFS序,后续问题会涉及此技巧,代码如下:
int a[N], k;
void dfs(int x)
{
a[k++] = x; //记录第一次访问x节点
vis[x] = true;
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
dfs(y);
}
a[k++] = x; //记录x节点回溯
}二叉树的先序
二叉树的中序
二叉树的后序
树的深度
树的深度是一种自顶向下的属性,我们可以在遍历的过程中结合递推记录下该属性,代码如下:
int d[N];
void dfs(int x)
{
vis[x] = true;
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
d[y] = d[x] + 1;//y是x的子节点,则深度等于父节点深度+1
dfs(y);
}
}树的重心
在介绍树的重心之前,我们先来介绍一下以每个节点x为根的子树大小size[x],这是一种自底向上的属性,求得每个节点对应的size代码如下:
int sz[N];
void dfs(int x)
{
vis[x] = true;
sz[x] = 1; //子树x的大小,包含其本身
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
dfs(y);
sz[x] += sz[y];
}
}树的重心是一个节点,对于节点x,把该节点删去后,原来的一颗树会划分成若干子树,记这些子树的最大sz等于max_part(x),那么重心p就是使得max_part(x)取得最小值的x,通过下面的代码我们可以得出p节点以及max_part(p):
int sz[N], ans = 0x3f3f3f3f, pos;
void dfs(int x)
{
int max_part = 0;
vis[x] = true;
sz[x] = 1; //子树x的大小,包含其本身
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
dfs(y);
sz[x] += sz[y];
max_part = max(max_part, sz[y]);
}
max_part = max(max_part, n - sz[x]);
if(max_part < ans)
{
pos = x;
ans = max_part;
}
}图的连通块划分
连通块,就是在一个子图中,任意两个点之间都存在一条路径,dfs每从x开始遍历,就会访问x能够到达的所有点与边,因此对N个节点做一次dfs就能划分出一张无向图中的各个连通块,或者是森林中的每课树,代码如下:
int vis[N], cnt;
//cnt记录了连通块的个数,同时也划分了每个点属于哪个连通块,vis[x]标记x属于第几个连通块
void dfs(int x)
{
vis[x] = cnt;
for(int i = h[x]; i != -1 ; i = ne[i])
{
int y = e[i];
if(vis[y]) continue;
dfs(y);
}
}
for(int i = 1 ; i <= n ; i ++)
{
if(vis[i]) continue;
cnt ++;
dfs(i);
}树与图的BFS,拓扑排序
树与图的BFS
我们用一个队列queue来实现,每次从队头取出一个节点x,沿着x节点往后走,把尚未访问过的节点加入队尾,代码如下:
int d[N];//用d[x]来表示节点在树中的深度,或者表示在图中x到起点的最少步数(+1)
void bfs()
{
memset(d, 0, sizeof d);
queue<int> q; q.push(1); d[1] = 1;
while(q.size())
{
int ver = q.front();
q.pop();
for(int i = head[ver], i != -1; i = ne[i])
{
int y = e[i];
if(d[y]) continue;
q.push(y);
d[y] = d[x] + 1;
}
}
}拓扑排序
给定一张有向无环图,存在这样一个由图中所有点构成的序列,对于图中的所有边x->y,x在A中都出现在y之前,则称A是该有向无环图的一个拓扑序列,可以证明有向无环图才至少存在一个拓扑序列,其求解方案如下:
- 预处理出所有点的入度deg[i],把所有入度为0的点加入队列中
- 取出队头节点x,把x加入拓扑序列seq的末尾
- 遍历x出发的所有边(x,y), 把deg[y] 减1,若被减为0,则把y入队
- 重复前面的过程,直到队列为空
我们每一次加入入度为0的点,就能保证在这个节点加入之前,没有任何节点有边指向该节点,如此便能保证拓扑序列的要求。
最后按顺序输出seq序列中的数字即可
// seq存储拓扑序列, deg记录每个点的入度
int seq[N], deg[N], cnt;
bool topsort()
{
queue<int> q;
for(int i = 1; i <= n ; i ++)
if(!deg[i]) q.push(i);
while(q.size())
{
int t = q.front();
q.pop();
seq[++cnt] = t;
for(int i = h[t]; i != -1; i = ne[i])
{
int y = e[i];
if(--deg[y] == 0) q.push(y);
}
}
return cnt == n;
}拓扑排序可以用来判断有向图中是否存在环,若seq的序列长度小于图中点的数量,就说明某些节点未被遍历,进而说明图中有环的存在,进一步的解释如下:
先来看一下求拓扑序列的算法, 我们每次--deg[i]实际就是擦除i这个节点的一条边的过程,而对于无环图来说,我们一定能擦除掉任何一个节点的所有入边。(如下图)
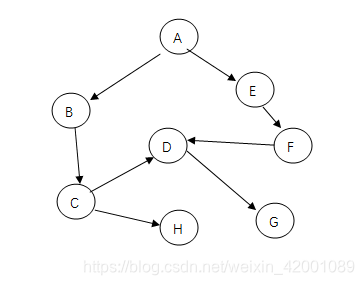
这是因为我们是自顶向下的擦除,取的是队列中的节点,并擦除该节点指向的节点的这条边,若存在环的话(如下图)
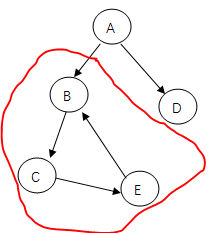
对于B这个点,入度为2,我们最多只能通过A节点擦除一条A->B的边,使其入度为1,之后就没有途径再使其入度减小,那么节点B就不会加入到队列中,继而就不会加入到拓扑序列中。