当两个数码表示数量大小时,可以进行加减乘除等算术运算。
一:两数绝对值之间的运算
加法运算:
二进制的每一位只有0和1两个数,低位向高位的进位关系是“逢二进一”,所以中的每一位的运算规则为:

减法运算:

乘法运算:

除法运算:
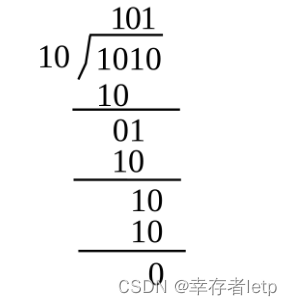
二:数字电路正负的表示及补码运算
1:正负数的表示方法(正->0 负->1)
二进制的原码表示法:+53 = (0 110101)
-53 = (1 110101)
2:二进制补码运算
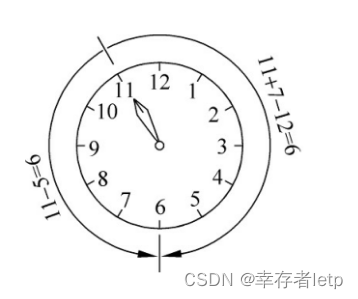
结论:在舍掉进位的情况下,两数相减(或符号不同的两数相加)可以用补码来实现。
举例:
1110 - 0110 = 1000 1110 + 1010 = 11000 = 1000(舍弃进位)
(14 - 6 = 8) (14 + 10 - 16 = 8)
0110 + 1010 = 2^4 >==> 1010是 -0110 对模2^4(16)的补码
( 6 + 10 = 16) 10 是 -6 对模2^4(16)的补码
3:二进制补码的表示方法(N指二进制数码)
当N为正数时:其原码、反码和补码等于原码。
当N为负数时:根据补码的运算规则 (N)comp = 2^n - N
二进制N的反码 (N)inv = (2^n - 1)-N
(N)inv +1 = (N)comp
二进制负数的补码等于反码加1
举例:计算二进制补码计算14-9
14:0 01110(原码 = 反码 = 补码)
-9:1 01001 (原码)
-9:1 10110 (反码)
-9:1 10111 (补码)

用补码相加得到的和仍是补码,如果想求负数的绝对值,应对它再求一次补码。
举例:计算二进制补码 -14-9
-9:1 10111 (补码)
-14:1 01110(原码)
-14:1 10001(反码)
-14:1 10010(补码)

三:“用补码相加得到的和仍是补码,如果想求负数的绝对值,应对它再求一次补码。”的详细讲解
在计算机中,负数通常使用补码表示。补码是表示负数的一种二进制编码方式。对于一个负数,求补码的方法是将它的二进制表示取反(即0变1,1变0),然后再加上1。
现在我们以一个负数 -5 作为例子来说明。-5 的二进制表示(补码)是 1011(负数的最高位为符号位,1 表示负数)。现在我们按照补码的求法来进行计算:
- 将 -5 的二进制表示取反,得到:0100。
- 将取反后的结果加上1,得到:0101。
所以,使用补码表示的 -5 的绝对值是 5,即 0101 的十进制表示。
因此,这句话的意思是,如果你想求一个负数的绝对值,可以先将该负数的二进制表示取反得到补码,然后再对补码再次进行取反运算,最后得到的结果就是该负数的绝对值。这是由于补码的性质,经过两次取反操作,负数转换成了正数。