🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝

📣系列专栏 - 机器学习【ML】自然语言处理【NLP】深度学习【DL】

🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

文章目录

使用蒙特卡洛方法计算 Pi

怎么做...

这个怎么运作...

还有更多...

也可以看看

执行蒙特卡罗政策评估

怎么做...

这个怎么运作...

还有更多...

用蒙特卡洛预测玩二十一点

怎么做...

这个怎么运作...

还有更多...

也可以看看

执行 on-policy Monte Carlo 控制

怎么做...

这个怎么运作...

还有更多...

使用 epsilon-greedy 策略开发 MC 控制

怎么做...

这个怎么运作...

执行离策略蒙特卡罗控制

怎么做...

这个怎么运作...

还有更多...

也可以看看

使用加权重要性采样开发 MC 控制

怎么做...

这个怎么运作...

还有更多...

也可以看看

在上一章中，我们使用动态规划( DP ) 评估并求解了马尔可夫决策过程( MDP )。DP 等基于模型的方法有一些缺点。它们要求环境是完全已知的，包括转换矩阵和奖励矩阵。它们的可扩展性也有限，尤其是对于具有大量状态的环境。

在本章中，我们将使用无模型方法继续我们的学习之旅，即蒙特卡洛( MC ) 方法，它不需要先验环境知识，并且比 DP 更具可扩展性。我们将从使用蒙特卡洛方法估计 Pi 的值开始。接下来，我们将讨论如何使用 MC 方法以 first-visit 和 every-visit 的方式预测状态值和状态动作值。我们将演示训练代理人使用蒙特卡洛玩二十一点纸牌游戏。此外，我们将实施 on-policy 和 off-policy MC 控制以找到 Blackjack 的最优策略。还将涵盖具有 epsilon-greedy 策略和加权重要性采样的高级 MC 控制。

本章将介绍以下食谱：

使用蒙特卡洛方法计算 Pi
执行蒙特卡罗政策评估
用蒙特卡洛预测玩二十一点
执行 on-policy Monte Carlo 控制
使用 epsilon-greedy 策略开发蒙特卡洛控制
执行离策略蒙特卡罗控制
使用加权重要性采样开发 MC 控制

使用蒙特卡洛方法计算 Pi

让我们从一个简单的项目开始：使用蒙特卡洛方法估计 π 的值，这是无模型强化学习算法的核心。

蒙特卡洛方法是任何使用随机性来解决问题的方法。该算法重复适当的随机抽样并观察符合特定属性的样本部分，以便进行数值估计。

让我们做一个有趣的练习，我们使用 MC 方法来近似 π 的值。我们将在一个宽度 = 2 (-1<x<1, -1<y<1) 的正方形中放置大量随机点，并计算有多少点落在单位半径的圆内。我们都知道正方形的面积是：

圆的面积是：

如果我们用圆的面积除以正方形的面积，我们有：

S/C可以通过落在圆内的点的分数来衡量。因此，π 的值可以估计为S/C的四倍。

怎么做...

我们使用 MC 方法估计 π 的值如下：

1.导入必要的模块，包括 PyTorch，math以获得 π 的真实值，并matplotlib绘制正方形中的随机点：

>>> import torch
>>> import math
>>> import matplotlib.pyplot as plt

2.我们在正方形内随机生成 1000 个点，范围为 -1<x<1 和 -1<y<1：

>>> n_point = 1000
>>> points = torch.rand((n_point, 2)) * 2 - 1

3.初始化落在单位圆内的点数，以及存储这些点的列表：

>>> n_point_circle = 0
>>> points_circle = []

4.对于每个随机点，计算到原点的距离。如果距离小于 1，则点落在圆内：

>>> for point in points:
...     r = torch.sqrt(point[0] ** 2 + point[1] ** 2)
...     if r <= 1:
...         points_circle.append(point)
...         n_point_circle += 1

5.计算圆圈中的点数并跟踪这些点：

>>> points_circle = torch.stack(points_circle)

6.绘制所有随机点并为圆圈中的随机点使用不同的颜色：

>>> plt.plot(points[:, 0].numpy(), points[:, 1].numpy(), 'y.')
>>> plt.plot(points_circle[:, 0].numpy(), points_circle[:, 1].numpy(), 'c.')

7.绘制圆圈以获得更好的可视化效果：

>>> i = torch.linspace(0, 2 * math.pi)
>>> plt.plot(torch.cos(i).numpy(), torch.sin(i).numpy())
>>> plt.axes().set_aspect('equal')
>>> plt.show()

8.最后，计算π的值：

>>> pi_estimated = 4 * (n_point_circle / n_point)
>>> print('Estimated value of pi is:', pi_estimated)

这个怎么运作...

在第 5 步中，您将看到以下图表，其中圆圈内随机放置点：

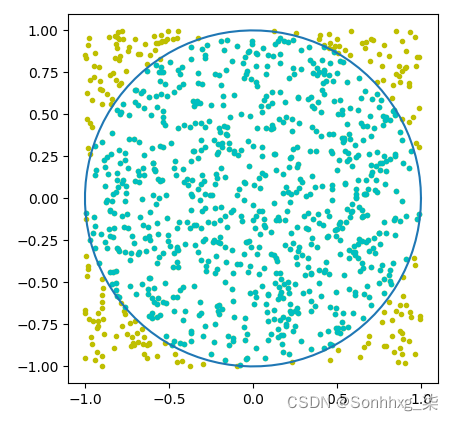
得益于大数定律( LLN ) ，蒙特卡洛方法如此强大。在 LLN 下，大量重复事件或动作的平均表现最终会收敛到期望值。在我们的例子中，有大量的随机点，4 * (n_point_circle / n_point)最终会收敛到 π 的真实值。

最后，在第 8 步中，我们打印 pi 的估计值，得到如下结果：

>>> estimate_pi_mc(10000)

使用蒙特卡洛方法近似的 π 值非常接近其真实值 (3.14159...)。

还有更多...

我们可以通过超过 1,000 次的迭代来进一步改进我们的估计。在这里，我们将试验 10,000 次迭代。在每次迭代中，我们在正方形中随机生成一个点，看它是否在圆中；我们根据落在圆内的现有点的比例动态估计 π 的值。

然后我们绘制估计历史以及 π 的真实值。将这些放入以下函数中：

>>> def estimate_pi_mc(n_iteration):
...     n_point_circle = 0
...     pi_iteration = []
...     for i in range(1, n_iteration+1):
...         point = torch.rand(2) * 2 - 1
...         r = torch.sqrt(point[0] ** 2 + point[1] ** 2)
...         if r <= 1:
...             n_point_circle += 1
...         pi_iteration.append(4 * (n_point_circle / i))
...     plt.plot(pi_iteration)
...     plt.plot([math.pi] * n_iteration, '--')
...     plt.xlabel('Iteration')
...     plt.ylabel('Estimated pi')
...     plt.title('Estimation history')
...     plt.show()
...     print('Estimated value of pi is:', pi_iteration[-1])

The estimated value of pi is: 3.1364

我们用 10,000 次迭代调用此函数：

>>> estimate_pi_mc(10000)

有关生成的估计历史记录，请参阅下图：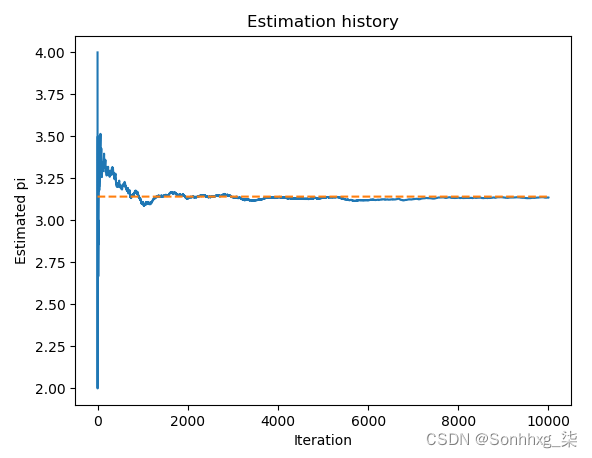

我们可以看到，随着迭代次数的增加，π 的估计值越来越接近真实值。事件或动作总是有一些变化。更多的重复可以帮助消除它。

也可以看看

如果您有兴趣了解蒙特卡洛方法的更多应用，这里有一些有趣的应用：

玩 Go、Havannah和Battleship等游戏，使用 MC 树搜索，搜索最佳着法：https ://en.wikipedia.org/wiki/Monte_Carlo_tree_search
评估投资和投资组合：https ://en.wikipedia.org/wiki/Monte_Carlo_methods_in_finance
使用 MC 模拟研究生物系统：https ://en.wikipedia.org/wiki/Bayesian_inference_in_phylogeny

执行蒙特卡罗政策评估

在第 2 章，马尔可夫决策过程和动态规划中，我们应用 DP 来执行策略评估，即策略的价值（或状态价值）函数。它工作得很好，但有一些限制。从根本上说，它需要一个完全已知的环境，包括转换矩阵和奖励矩阵。然而，大多数现实生活中的转移矩阵是事先不知道的。需要已知 MDP 的强化学习算法被归类为基于模型的算法。另一方面，不需要转换和奖励先验知识的算法称为无模型算法。基于蒙特卡罗的强化学习是一种无模型的方法。

在这个秘籍中，我们将使用蒙特卡洛方法评估价值函数。我们将再次以 FrozenLake 环境为例，假设我们无法同时访问其转换矩阵和奖励矩阵。你会记得一个过程的回报，即长期的总回报，如下所示：

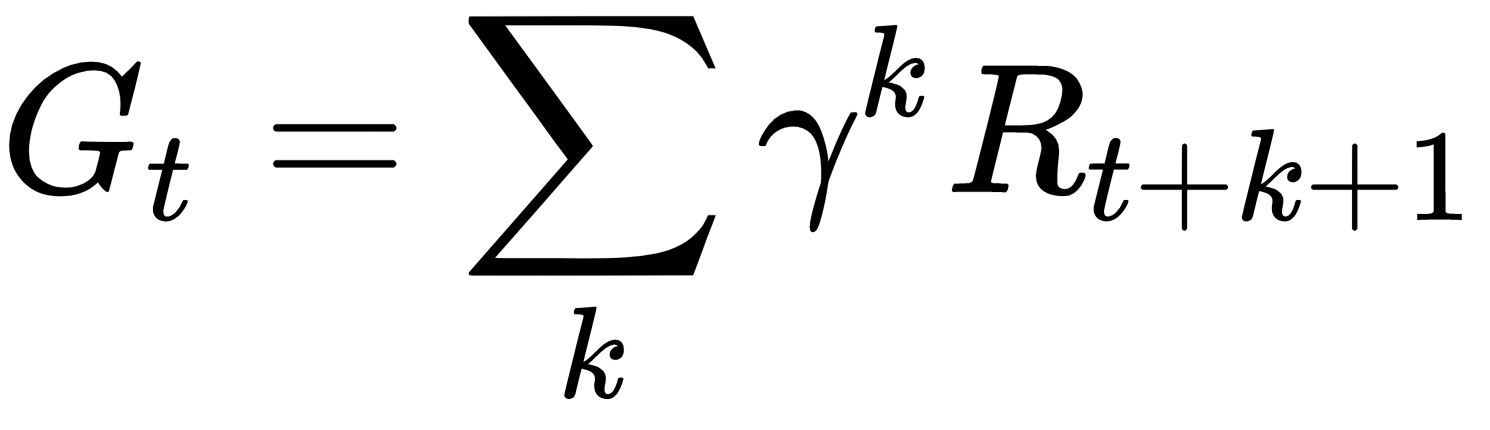
MC 政策评估使用经验平均 回报而不是预期回报（如在 DP 中）来估计价值函数。有两种方法可以执行 MC 策略评估。一个是首次访问 MC 预测，它仅对情节中第一次出现状态 s的回报进行平均。另一个是every-visit MC prediction ，它对一个情节中每次出现状态s的回报进行平均。显然，first-visit MC prediction 的计算量比 every-visit 版本少很多，因此使用频率更高。

怎么做...

我们对 FrozenLake 的最优策略执行首次访问 MC 预测，如下所示：

1.导入 PyTorch 和 Gym 库，并创建 FrozenLake 环境的实例：

>>> import torch
>>> import gym
>>> env = gym.make("FrozenLake-v0")

2.要使用蒙特卡洛方法评估策略，我们首先需要定义一个函数来模拟给定策略的 FrozenLake 情节并返回每个步骤的奖励和状态：

>>> def run_episode(env, policy):
 ...     state = env.reset()
 ...     rewards = []
 ...     states = [state]
 ...     is_done = False
 ...     while not is_done:
 ...         action = policy[state].item()
 ...         state, reward, is_done, info = env.step(action)
 ...         states.append(state)
 ...         rewards.append(reward)
 ...         if is_done:
 ...             break
 ...     states = torch.tensor(states)
 ...     rewards = torch.tensor(rewards)
 ...     return states, rewards

同样，在蒙特卡罗设置中，我们需要跟踪所有步骤的状态和奖励，因为我们无法访问完整的环境，包括转移概率和奖励矩阵。

3.现在，定义使用首次访问 MC 评估给定策略的函数：

>>> def mc_prediction_first_visit(env, policy, gamma, n_episode):
...     n_state = policy.shape[0]
...     V = torch.zeros(n_state)
...     N = torch.zeros(n_state)
...     for episode in range(n_episode):
...         states_t, rewards_t = run_episode(env, policy)
...         return_t = 0
...         first_visit = torch.zeros(n_state)
...         G = torch.zeros(n_state)
...         for state_t, reward_t in zip(reversed(states_t)[1:], 
                                            reversed(rewards_t)):
...             return_t = gamma * return_t + reward_t
...             G[state_t] = return_t
...             first_visit[state_t] = 1
...         for state in range(n_state):
...             if first_visit[state] > 0:
...                 V[state] += G[state]
...                 N[state] += 1
...     for state in range(n_state):
...         if N[state] > 0:
...             V[state] = V[state] / N[state]
...     return V

4.我们将折扣率指定为 1 以便于计算，并模拟 10,000 集：

>>> gamma = 1
>>> n_episode = 10000

5.我们使用在上一章马尔可夫 决策过程和动态规划中计算出的最优策略，并将其连同其他参数一起提供给首次访问 MC 函数：

>>> optimal_policy = torch.tensor([0., 3., 3., 3., 0., 3., 2., 3., 3., 1., 0., 3., 3., 2., 1., 3.])
>>> value = mc_prediction_first_visit(env, optimal_policy, gamma, n_episode)
>>> print('The value function calculated by first-visit MC prediction:\n', value)
The value function calculated by first-visit MC prediction:
tensor([0.7463, 0.5004, 0.4938, 0.4602, 0.7463, 0.0000, 0.3914, 0.0000, 0.7463, 0.7469, 0.6797, 0.0000, 0.0000, 0.8038, 0.8911, 0.0000])

我们刚刚使用首次访问 MC 预测求解了最优策略的价值函数。

这个怎么运作...

在第 3 步中，我们在 MC 预测中执行以下任务：

我们运行n_episode剧集
对于每一集，我们计算每个状态的第一次访问的回报
对于每个状态，我们通过平均所有情节的第一次回报来获得价值

如您所见，在基于 MC 的预测中，无需了解环境的完整模型。事实上，在大多数现实世界的情况下，转移矩阵和奖励矩阵是事先不知道的，或者是极难获得的。想象一下下棋或围棋有多少种可能的状态，有多少种可能的动作；几乎不可能计算出转换矩阵和奖励矩阵。无模型强化学习是通过与环境交互从经验中学习。

在我们的案例中，我们只考虑了可以观察到的内容，包括每一步的新状态和奖励，并使用蒙特卡罗方法进行预测。请注意，我们模拟的情节越多，我们可以获得的预测就越准确。如果绘制每集更新后的值，您将看到它如何随时间收敛，这类似于我们在估计 π 值时看到的情况。

还有更多...

我们决定还对 FrozenLake 的最优策略执行每次访问 MC 预测：

1.我们定义了使用每次访问 MC 评估给定策略的函数：

>>> def mc_prediction_every_visit(env, policy, gamma, n_episode):
...     n_state = policy.shape[0]
...     V = torch.zeros(n_state)
...     N = torch.zeros(n_state)
...     G = torch.zeros(n_state)
...     for episode in range(n_episode):
...         states_t, rewards_t = run_episode(env, policy)
...         return_t = 0
...         for state_t, reward_t in zip(reversed(states_t)[1:],  
                                            reversed(rewards_t)):
...             return_t = gamma * return_t + reward_t
...             G[state_t] += return_t
...             N[state_t] += 1
...     for state in range(n_state):
...         if N[state] > 0:
...             V[state] = G[state] / N[state]
...     return V

与首次访问 MC 类似，每次访问函数执行以下任务：

它运行n_episode剧集
对于每一集，它计算每次访问状态的回报
对于每个状态，它通过平均所有情节的所有回报来获得价值

2.通过在函数中提供策略和其他参数来计算值：

>>> value = mc_prediction_every_visit(env, optimal_policy, gamma, n_episode)

3.显示结果值：

>>> print('The value function calculated by every-visit MC prediction:\n', value)
The value function calculated by every-visit MC prediction:
tensor([0.6221, 0.4322, 0.3903, 0.3578, 0.6246, 0.0000, 0.3520, 0.0000, 0.6428, 0.6759, 0.6323, 0.0000, 0.0000, 0.7624, 0.8801, 0.0000])

用蒙特卡洛预测玩二十一点

在这个秘籍中，我们将玩二十一点（也称为 21）并评估我们认为可能有效的策略。您将通过 Blackjack 示例更加熟悉 Monte Carlo 预测，并准备好在接下来的食谱中使用 Monte Carlo 控制搜索最优策略。

二十一点是一种流行的纸牌游戏，其目标是使纸牌总数尽可能接近 21 点而不超过它。J、K、Q牌的点数为10，2到10的牌点数为2到10。A牌可以是1点，也可以是11点；when the latter value is chosen, it is called a usable ace. 玩家与庄家竞争。开始时，双方随机获得两张牌，但只有庄家的一张牌展示给玩家。玩家可以请求额外的牌（称为hit）或停止接收更多牌（称为stick）。闲家出牌后，庄家继续抓牌，直到牌面总和大于等于17。闲家出牌前，如果他们的牌的总和超过 21（称为 going bust），则玩家输了。否则，如果庄家的牌总数超过 21，则玩家获胜。

如果双方都没有爆牌，得分最高的一方获胜，也可能平局。Gym 中的 Blackjack 环境制定如下：

Blackjack 有限 MDP 的一集开始时双方各有两张牌，并且只观察庄家的一张牌。
一集以任何一方获胜或双方平局结束。如果玩家获胜，一集的最终奖励为 +1，如果他们输了，则为 -1，如果平局则为 0。
在每一轮中，玩家可以采取两个动作，打（1）和棒（0），意思是要求另一张牌和要求不再收到任何牌。

我们将首先尝试一个简单的策略，只要总点数小于 18（或者 19 或 20，如果您愿意），我们就会不断添加新卡片。

怎么做...

让我们从模拟 Blackjack 环境并探索其状态和动作开始：

1.导入 PyTorch 和 Gym，并创建一个Blackjack实例：

>>> import torch
>>> import gym
>>> env = gym.make('Blackjack-v0')

2.重置环境：

>>> env.reset() 
>>> env.reset() 
(20, 5, False)

它返回三个状态变量：

玩家的点数（20在这个例子中）
经销商的积分（5在本例中）
玩家是否有可用的 A（False在本例中）

可用的 A 意味着玩家拥有可以算作 11 的 A 而不会爆牌。如果玩家没有 A，或有 A 但爆牌，则状态参数将变为False.

看看下面的情节：

>>> env.reset() 
(18, 6, True)

18 点True意味着玩家有一张 A 和一张 7，A 算作 11。

3.让我们采取一些行动，看看 Blackjack 环境是如何工作的。首先，由于我们有一张可用的 A，它提供了一些灵活性，因此我们受到了打击（请求一张额外的牌）：

>>> env.step(1) 
((20, 6, True), 0, False, {})

这将返回三个状态变量(20, 6, True)，一个奖励（0目前），以及情节是否结束（False目前）。

然后我们停止抽牌：

>>> env.step(0) 
 ((20, 6, True), 1, True, {})

我们刚刚在这一集中赢了，因此奖励是1，现在这一集结束了。同样，一旦玩家呼叫stick，庄家就会采取行动。

4.有时我们会输；例如：

>>> env.reset()
(15, 10, False)
>>> env.step(1)
((25, 10, False), -1, True, {})

接下来，我们将预测一个简单策略的值，即当分数达到 18 时我们停止添加新卡片：

5.与往常一样，我们首先需要定义一个函数，在一个简单的策略下模拟 Blackjack 情节：

>>> def run_episode(env, hold_score):
 ...     state = env.reset()
 ...     rewards = []
 ...     states = [state]
 ...     is_done = False
 ...     while not is_done:
 ...         action = 1 if state[0] < hold_score else 0
 ...         state, reward, is_done, info = env.step(action)
 ...         states.append(state)
 ...         rewards.append(reward)
 ...         if is_done:
 ...             break
 ...     return states, rewards

6.现在，我们定义了一个函数，用于评估具有首次访问 MC 的简单 Blackjack 策略：

>>> from collections import defaultdict
>>> def mc_prediction_first_visit(env, hold_score, gamma, 
                                                 n_episode):
 ...     V = defaultdict(float)
 ...     N = defaultdict(int)
 ...     for episode in range(n_episode):
 ...         states_t, rewards_t = run_episode(env, hold_score)
 ...         return_t = 0
 ...         G = {}
 ...         for state_t, reward_t in zip(states_t[1::-1], 
                                             rewards_t[::-1]):
 ...             return_t = gamma * return_t + reward_t
 ...             G[state_t] = return_t
 ...         for state, return_t in G.items():
 ...             if state[0] <= 21:
 ...                 V[state] += return_t
 ...                 N[state] += 1
 ...     for state in V:
 ...         V[state] = V[state] / N[state]
 ...     return V

7.我们指定hold_score为 18，贴现率为 1，并模拟 500,000 集：

>>> hold_score = 18 
>>> gamma = 1 
>>> n_episode = 500000

8.现在，让我们通过插入所有变量来执行 MC 预测：

>>> value = mc_prediction_first_visit(env, hold_score, gamma, n_episode)

我们尝试打印结果值函数：

>>> print('The value function calculated by first-visit MC prediction:\n', value)

我们刚刚计算了所有可能状态的值：

>>> print('Number of states:', len(value))
Number of states: 280

总共有280个州。

这个怎么运作...

如您所见，在第 4 步中，我们的点数超过了 21，因此我们输了。同样，Blackjack 中的状态实际上是一个三元素元组。第一个元素是玩家的分数；第二个元素是从庄家牌组中翻开的牌，它的点数可以从 1 到 10；第三个要素是关于是否拥有可重复使用的王牌。

值得注意的是，在第 5 步中，在每一轮的 episode 中，agent 根据当前分数进行命中或坚持，如果小于则坚持hold_score，否则接受打击。同样，在蒙特卡罗设置中，我们跟踪所有步骤的状态和奖励。

执行步骤 8中的代码行，您将看到以下结果：

The value function calculated by first-visit MC prediction:
defaultdict(<class 'float'>, {(20, 6, False): 0.6923485653560042, (17, 5, False): -0.24390243902439024, (16, 5, False): -0.19118165784832453, (20, 10, False): 0.4326379146490474, (20, 7, False): 0.7686220540168588, (16, 6, False): -0.19249478804725503,
 ……
 ……
(5, 9, False): -0.20612244897959184, (12, 7, True): 0.058823529411764705, (6, 4, False): -0.26582278481012656, (4, 8, False): -0.14937759336099585, (4, 3, False): -0.1680327868852459, (4, 9, False): -0.20276497695852536, (4, 4, False): -0.3201754385964912, (12, 8, True): 0.11057692307692307})

我们刚刚体验了使用 MC 预测在 Blackjack 环境中计算 280 个状态的价值函数是多么有效。在步骤 2的 MC 预测函数中，我们执行了以下任务：

我们n_episode在简单的二十一点政策下运行剧集
对于每一集，我们计算每个州第一次访问的回报
对于每个状态，我们通过平均所有情节的第一次回报来获得价值

请注意，我们忽略玩家总和大于 21 的状态，因为我们知道它们都将是 -1。

Blackjack 环境的模型，包括转换矩阵和奖励矩阵，是事先不知道的。此外，获得两个状态之间的转移概率非常昂贵。事实上，转换矩阵的大小为 280 * 280 * 2，这将需要大量计算。在基于 MC 的解决方案中，我们只需要模拟足够的情节，并为每个情节计算回报并相应地更新价值函数。

下次您使用简单策略（如果总和达到一定水平就坚持）玩 Blackjack 时，使用预测值来决定在每场游戏中出价多少会很有趣。

还有更多...

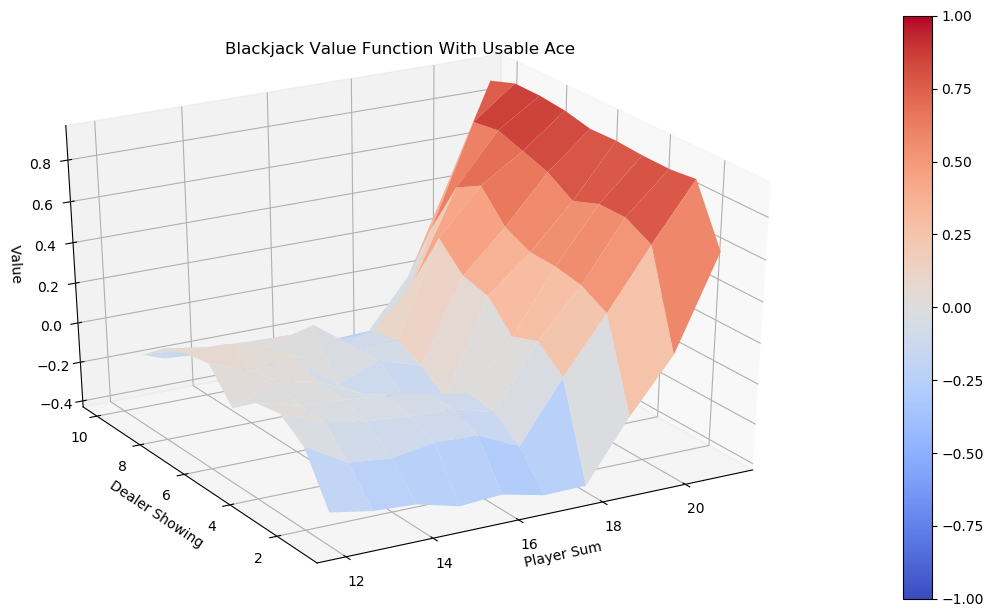
因为在这种情况下有很多状态，所以很难一一读取它们的值。我们实际上可以通过制作三维曲面图来可视化价值函数。状态是三维的，第三维有两种可能的选择（有或没有可用的王牌）。我们可以将我们的图分成两部分：一部分用于具有可用 A 的状态，另一部分用于没有可用 A 的状态。在每个图中，x轴是玩家的总和，y轴是庄家翻开的牌，z轴是值。

让我们按照以下步骤来创建可视化：

1.在 matplotlib 中导入所有必要的模块以进行可视化：

>>> import matplotlib
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D

2.定义创建 3D 曲面图的效用函数：

>>> def plot_surface(X, Y, Z, title):
...     fig = plt.figure(figsize=(20, 10))
...     ax = fig.add_subplot(111, projection='3d')
...     surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
...             cmap=matplotlib.cm.coolwarm, vmin=-1.0, vmax=1.0)
...     ax.set_xlabel('Player Sum')
...     ax.set_ylabel('Dealer Showing')
...     ax.set_zlabel('Value')
...     ax.set_title(title)
...     ax.view_init(ax.elev, -120)
...     fig.colorbar(surf)
...     plt.show()

3.接下来，我们定义一个函数，该函数构建要沿三个维度绘制的数组，并调用plot_surface以分别使用和不使用可用 ace 来可视化值：

>>> def plot_blackjack_value(V):
...     player_sum_range = range(12, 22)
...     dealer_show_range = range(1, 11)
...     X, Y = torch.meshgrid([torch.tensor(player_sum_range), 
                torch.tensor(dealer_show_range)])
...     values_to_plot = torch.zeros((len(player_sum_range),  
                                  len(dealer_show_range), 2))
...     for i, player in enumerate(player_sum_range):
...         for j, dealer in enumerate(dealer_show_range):
...             for k, ace in enumerate([False, True]):
...                 values_to_plot[i, j, k] = 
                               V[(player, dealer, ace)]
...     plot_surface(X, Y, values_to_plot[:,:,0].numpy(), 
                "Blackjack Value Function Without Usable Ace")
...     plot_surface(X, Y, values_to_plot[:,:,1].numpy(), 
                "Blackjack Value Function With Usable Ace")

我们只对查看玩家得分超过 11 的状态感兴趣，我们创建了一个values_to_plot张量来存储这些值。

4.最后，我们调用plot_blackjack_value函数：

>>> plot_blackjack_value(value)

没有可用 ace 的状态的结果值图如下：

具有可用 ace 的状态的价值函数可视化如下：

随意尝试一下的值，hold_score看看它如何影响价值函数。

也可以看看

如果您不熟悉 Blackjack 环境，可以从https://github.com/openai/gym/blob/master/gym/envs/toy_text/blackjack.py的源代码了解更多信息。

有时，阅读代码比阅读简单的英文描述更容易。

执行 on-policy Monte Carlo 控制

在前面的秘籍中，我们预测了如果分数达到 18，代理将保持的策略的价值。这是一个简单的策略，每个人都可以轻松想出，尽管显然不是最优策略。在这个秘籍中，我们将使用 on-policy Monte Carlo控制来搜索玩 Blackjack 的最优策略。

蒙特卡罗预测用于评估给定策略的价值，而蒙特卡罗控制（MC 控制）用于在未给出此类策略时寻找最优策略。基本上有 MC 控制的类别：on-policy 和 off-policy。在策略方法通过执行策略并评估和改进策略来学习最优策略，而离策略方法使用另一个策略生成的数据来学习最优策略。on-policy MC控制的工作方式与动态规划中的策略迭代非常相似，它有两个阶段，评估和改进：

在评估阶段，它评估的不是价值函数（也称为状态价值或效用），而是行动价值。动作值更常被称为Q 函数，它是状态动作对(s, a)在给定策略下通过在状态s中采取动作 a的效用。同样，可以以首次访问方式或每次访问方式进行评估。
在改进阶段，通过为每个状态分配最佳动作来更新策略：

最优策略将通过交替两个阶段进行大量迭代来获得。

怎么做...

让我们通过执行以下步骤来搜索具有 on-policy MC 控制的最佳 Blackjack 策略：

1.导入必要的模块并创建一个 Blackjack 实例：

>>> import torch
>>> import gym
>>> env = gym.make('Blackjack-v0')

2.接下来，让我们开发一个运行剧集并在 Q 函数下执行操作的函数。这是改进阶段：

>>> def run_episode(env, Q, n_action):
 ...     """
 ...     运行一个给定Q函数的剧集
 ...     @param env: OpenAI Gym environment 
 ...     @param Q: Q-function 
 ...     @param n_action：动作空间
 ...     @return：整个情节的结果状态、动作和奖励
 ...     """
 ...     state = env.reset()
 ...     rewards = []
 ...     actions = []
 ...     states = []
 ...     is_done = False
 ...     action = torch.randint(0, n_action, [1]).item()
 ...     while not is_done:
 ...         actions.append(action)
 ...         states.append(state)
 ...         state, reward, is_done, info = env.step(action)
 ...         rewards.append(reward)
 ...         if is_done:
 ...             break
 ...         action = torch.argmax(Q[state]).item()
 ...     return states, actions, rewards

3.现在，我们开发 on-policy MC 控制算法：

 >>> from collections import defaultdict
 >>> def mc_control_on_policy(env, gamma, n_episode):
 ...     """
 ...     以 on-policy MC 控制方式获取最优策略
 ...     @param env: OpenAI Gym 环境
 ...     @param gamma：折扣因子
 ...     @param n_episode：剧集数
 ...     @return：最优 Q 函数和最优策略
 ...     """
 ...     n_action = env.action_space.n
 ...     G_sum = defaultdict(float)
 ...     N = defaultdict(int)
 ...     Q = defaultdict(lambda: torch.empty(env.action_space.n))
 ...     for episode in range(n_episode):
 ...         states_t, actions_t, rewards_t = run_episode(env, Q,
                                               n_action) 
 ...         return_t = 0
 ...         G = {}
 ...         for state_t, action_t, reward_t in zip(states_t[::-1], 
                     actions_t[::-1], rewards_t[::-1]):
 ...             return_t = gamma * return_t + reward_t
 ...             G[(state_t, action_t)] = return_t
 ...         for state_action, return_t in G.items():
 ...             state, action = state_action
 ...             if state[0] <= 21:
 ...                 G_sum[state_action] += return_t
 ...                 N[state_action] += 1
 ...                 Q[state][action] = G_sum[state_action] 
                                         / N[state_action]
 ...      policy = {}
 ...      for state, actions in Q.items():
 ...          policy[state] = torch.argmax(actions).item()
 ...      return Q, policy

4.我们将折扣率指定为 1，并将使用 500,000 集：

>>> gamma = 1
>>> n_episode = 500000

5.执行 on-policy MC 控制以获得最优 Q 函数和策略：

>>> optimal_Q, optimal_policy = mc_control_on_policy(env, gamma, n_episode)
>>> print(optimal_policy)

6.我们还可以计算最优策略的价值函数并打印出最优值，如下所示：

>>> optimal_value = defaultdict(float)
>>> for state, action_values in optimal_Q.items():
 ...     optimal_value[state] = torch.max(action_values).item()
>>> print(optimal_value)

7.可视化使用的值plot_blackjack_value和plot_surface我们在上一节中开发的函数，使用蒙特卡洛预测玩二十一点：

>>> plot_blackjack_value(optimal_value)

这个怎么运作...

在这个秘籍中，我们通过探索开始来解决带有策略 MC 控制的 Blackjack 游戏。这通过在我们模拟的每个情节中交替进行评估和改进来实现我们的策略优化目标。

在第 2 步中，我们运行一个情节并通过执行以下任务在 Q 函数下采取行动：

我们初始化一个情节。
我们采取随机行动作为探索的开始。
在第一个动作之后，我们根据当前的 Q 函数采取动作，即。
我们记录情节中所有步骤的状态、动作和奖励，这些将在评估阶段使用。

重要的是要注意第一个动作是随机选择的，因为 MC 控制算法只会在这种情况下收敛到最优解。在 MC 算法中以随机动作开始一集称为探索开始。

在探索开始设置中，随机选择情节中的第一个动作，以确保策略收敛到最优解。否则，一些状态永远不会被访问，因此它们的状态-动作值永远不会被优化，最终策略将变得次优。

步骤2是改进阶段，步骤3是MC控制，我们执行以下任务：

使用任意小值初始化 Q 函数。
运行n_episode剧集。
对于每个episode，进行policy improvement，获取state、actions、reward；并根据结果状态、动作和奖励使用首次访问 MC 预测执行策略评估，从而更新 Q 函数。
最后确定最优Q函数，通过对最优Q函数中的每个状态采取最佳动作得到最优策略。

在每次迭代中，我们通过针对当前动作值函数 Q（即）采取最佳动作来使策略变得贪婪。结果，即使我们以任意策略开始，我们也将能够获得最优策略。

在第5步，可以看到生成的最优策略，如下：

{(16, 8, True): 1, (11, 2, False): 1, (15, 5, True): 1, (14, 9, False): 1, (11, 6, False): 1, (20, 3, False): 0, (9, 6, False): 0, (12, 9, False): 0, (21, 2, True): 0, (16, 10, False): 1, (17, 5, False): 0, (13, 10, False): 1, (12, 10, False): 1, (14, 10, False): 0, (10, 2, False): 1, (20, 4, False): 0, (11, 4, False): 1, (16, 9, False): 0, (10, 8,
 ……
 ……
1, (18, 6, True): 0, (12, 2, True): 1, (8, 3, False): 1, (13, 3, True): 0, (4, 7, False): 1, (18, 8, True): 0, (6, 5, False): 1, (17, 6, True): 0, (19, 9, True): 0, (4, 4, False): 0, (14, 5, True): 1, (12, 6, True): 0, (4, 9, False): 1, (13, 4, True): 1, (4, 8, False): 1, (14, 3, True): 1, (12, 4, True): 1, (4, 6, False): 0, (12, 5, True): 0, (4, 2, False): 1, (4, 3, False): 1, (5, 4, False): 1, (4, 1, False): 0}

在第 6 步中，您可以看到最优策略的结果值，如下所示：

{(21, 8, False): 0.9262458682060242, (11, 8, False): 0.16684606671333313, (16, 10, False): -0.4662476181983948, (16, 10, True): -0.3643564283847809, (14, 8, False): -0.2743947207927704, (13, 10, False): -0.3887477219104767, (12, 9, False): -0.22795115411281586
 ……
 ……
(4, 3, False): -0.18421052396297455, (4, 8, False): -0.16806723177433014, (13, 2, True): 0.05485232174396515, (5, 5, False): -0.09459459781646729, (5, 8, False): -0.3690987229347229, (20, 2, True): 0.6965699195861816, (17, 2, True): -0.09696969389915466, (12, 2, True): 0.0517241396009922}

在第 7 步中，您将看到没有可用 ace 的状态的结果值图，如下所示：

具有可用 ace 的状态的价值函数可视化如下：

还有更多...

您可能想知道最优策略是否真的比简单策略更有效。现在让我们分别在最优策略和简单策略下模拟 100,000 个 Blackjack 情节。我们将比较两种策略的获胜和失败机会：

1.首先，我们定义简单的策略，当分数达到 18 时采取摇杆动作：

>>> hold_score = 18
>>> hold_policy = {}
>>> player_sum_range = range(2, 22)
>>> for player in range(2, 22):
...     for dealer in range(1, 11):
...         action = 1 if player < hold_score else 0
...         hold_policy[(player, dealer, False)] = action
...         hold_policy[(player, dealer, True)] = action

2.接下来，我们定义一个包装函数，它在给定策略下运行一集并返回最终奖励：

>>> def simulate_episode(env, policy):
...     state = env.reset()
...     is_done = False
...     while not is_done:
...         action = policy[state]
...         state, reward, is_done, info = env.step(action)
...         if is_done:
...             return reward

3.然后，我们指定集数（100,000），并开始计算输赢：

>>> n_episode = 100000 
>>> n_win_optimal = 0 
>>> n_win_simple = 0 
>>> n_lose_optimal = 0 
>>> n_lose_simple = 0

4.然后，我们运行 100,000 集并跟踪输赢：

>>> for _ in range(n_episode):
...     reward = simulate_episode(env, optimal_policy)
...     if reward == 1:
...         n_win_optimal += 1
...     elif reward == -1:
...         n_lose_optimal += 1
...     reward = simulate_episode(env, hold_policy)
...     if reward == 1:
...         n_win_simple += 1
...     elif reward == -1:
...         n_lose_simple += 1

5.最后，我们打印出我们得到的结果：

>>> print('Winning probability under the simple policy: {}'.format(n_win_simple/n_episode))
Winning probability under the simple policy: 0.39923
>>> print('Winning probability under the optimal policy: {}'.format(n_win_optimal/n_episode))
Winning probability under the optimal policy: 0.41281

在最优策略下玩有 41.28% 的机会获胜，而在简单策略下玩有 39.92% 的机会。那么，我们输的概率是：

>>> print('Losing probability under the simple policy: {}'.format(n_lose_simple/n_episode))
Losing probability under the simple policy: 0.51024
>>> print('Losing probability under the optimal policy: {}'.format(n_lose_optimal/n_episode))
Losing probability under the optimal policy: 0.493

另一方面，在最优策略下玩有 49.3% 的机会输，而在简单策略下玩有 51.02% 的机会。

我们的最优策略显然是赢家！

使用 epsilon-greedy 策略开发 MC 控制

在前面的秘籍中，我们使用带有贪婪搜索的 MC 控制来搜索最优策略，其中选择了具有最高状态-动作值的动作。但是，早期情节中可用的最佳选择并不能保证最佳解决方案。如果我们只关注暂时最好的选择而忽略了整体问题，我们将陷入局部最优，而不是达到全局最优。解决方法是 epsilon-greedy 策略。

在epsilon-greedy policy 的MC control 中，我们不再一直利用最佳动作，而是在一定的概率下随机选择一个动作。顾名思义，该算法有两个方面：

Epsilon：给定参数 ε，其值介于0和1之间，执行每个动作的概率计算如下：

这里，|A| 是可能动作的数量。

贪心：state-action 值最高的动作受到青睐，其被选中的概率增加1-ε：

Epsilon-greedy policy 大部分时间都采用最佳动作，并且不时地探索不同的动作。

怎么做...

让我们使用 epsilon-greedy 策略解决 Blackjack 环境：

1.导入必要的模块并创建一个 Blackjack 实例：

>>> import torch
>>> import gym
>>> env = gym.make('Blackjack-v0')

2.接下来，让我们开发一个运行剧集并执行 epsilon-greedy 的函数：

>>> def run_episode(env, Q, epsilon, n_action):
...     """
...     运行一集并执行 epsilon-greedy 策略
...     @param env: OpenAI Gym 环境
...     @param Q: Q函数
...     @param epsilon：探索和开发之间的权衡
...     @param n_action：动作空间
...     @return：整个情节的结果状态，动作和奖励
...     """
...     state = env.reset()
...     rewards = []
...     actions = []
...     states = []
...     is_done = False
...     while not is_done:
...         probs = torch.ones(n_action) * epsilon / n_action
...         best_action = torch.argmax(Q[state]).item()
...         probs[best_action] += 1.0 - epsilon
...         action = torch.multinomial(probs, 1).item()
...         actions.append(action)
...         states.append(state)
...         state, reward, is_done, info = env.step(action)
...         rewards.append(reward)
...         if is_done:
...             break
...     return states, actions, rewards

3.现在，使用 epsilon-greedy 开发 on-policy MC 控制：

>>> from collections import defaultdict
>>> def mc_control_epsilon_greedy(env, gamma, n_episode, epsilon):
...     """
...     Obtain the optimal policy with on-policy MC control with epsilon_greedy
...     @param env: OpenAI Gym environment
...     @param gamma: discount factor
...     @param n_episode: number of episodes
...     @param epsilon: the trade-off between exploration and exploitation
...     @return: the optimal Q-function, and the optimal policy
...     """
...     n_action = env.action_space.n
...     G_sum = defaultdict(float)
...     N = defaultdict(int)
...     Q = defaultdict(lambda: torch.empty(n_action))
...     for episode in range(n_episode):
...         states_t, actions_t, rewards_t = 
                     run_episode(env, Q, epsilon, n_action)
...         return_t = 0
...         G = {}
...         for state_t, action_t, reward_t in zip(states_t[::-1], 
                                 actions_t[::-1], rewards_t[::-1]):
...             return_t = gamma * return_t + reward_t
...             G[(state_t, action_t)] = return_t
...         for state_action, return_t in G.items():
...             state, action = state_action
...             if state[0] <= 21:
...                 G_sum[state_action] += return_t
...                 N[state_action] += 1
...                 Q[state][action] = 
                         G_sum[state_action] / N[state_action]
...     policy = {}
...     for state, actions in Q.items():
...         policy[state] = torch.argmax(actions).item()
...     return Q, policy

4.我们将贴现率指定为 1，ε 为 0.1，并将使用 500,000 集：

>>> gamma = 1
>>> n_episode = 500000
>>> epsilon = 0.1

5.使用 epsilon-greedy 策略执行 MC 控制以获得最优 Q 函数和策略：

>>> optimal_Q, optimal_policy = mc_control_epsilon_greedy(env, gamma, n_episode, epsilon)

随意打印出最优值并使用我们开发plot_blackjack_value的函数将其可视化。plot_surface我们在此不再重复该过程。

6.最后，我们想知道 epsilon-greedy 方法是否真的更有效。同样，我们在 epsilon-greedy 生成的最优策略下模拟 100,000 个 Blackjack 情节并计算获胜和失败的机会：

>>> n_episode = 100000
>>> n_win_optimal = 0
>>> n_lose_optimal = 0
>>> for _ in range(n_episode):
...     reward = simulate_episode(env, optimal_policy)
...     if reward == 1:
...         n_win_optimal += 1
...     elif reward == -1:
...         n_lose_optimal += 1

在这里，我们重用了simulate_episode上一节中的函数。

这个怎么运作...

在这个秘籍中，我们使用 epsilon-greedy 的策略 MC 控制来解决 Blackjack 游戏。

在第 2 步中，我们运行一个 episode 并使用以下任务执行 epsilon-greedy：

我们初始化一个情节。
我们计算选择单个动作的概率：对于基于当前 Q 函数的最佳动作，概率为，否则概率为。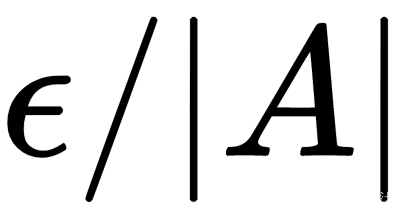
我们记录情节中所有步骤的状态、动作和奖励，这些将在评估阶段使用。

Epsilon-greedy 通过利用概率为的最佳动作优于贪婪搜索方法，同时允许以的概率随机探索其他动作。超参数 ε 是开发和探索之间的权衡。如果它的值为 0，则算法变得完全贪婪；如果该值为1，则平均选择每个动作，因此该算法只是进行随机探索。

ε 的值需要根据实验进行调整，没有一个普适的值对所有实验都最好。话虽如此，一般来说，我们可以选择 0.1、0.2 或 0.3 开始。另一种方法是从稍大的值（例如 0.5 或 0.7）开始，然后随着时间的推移逐渐减小（例如，每集衰减 0.999）。这样一来，该政策将在开始时专注于探索不同的行动，随着时间的推移，它将倾向于利用好的行动。

最后，在执行第 6 步之后，对 100,000 集的结果进行平均并打印获胜概率，我们现在有以下内容：

>>> print('Winning probability under the optimal policy: {}'.format(n_win_optimal/n_episode))
Winning probability under the optimal policy: 0.42436

通过 epsilon-greedy 方法获得的最优策略有 42.44% 的获胜机会，高于没有 epsilon-greedy 的获胜机会（41.28%）。

然后，我们还打印失败概率：

>>> print('Losing probability under the optimal policy: {}'.format(n_lose_optimal/n_episode))
Losing probability under the optimal policy: 0.48048

如您所见，使用 epsilon-greedy 方法失败的几率较低（48.05% 对比没有 epsilon-greedy 的 49.3%）。

执行离策略蒙特卡罗控制

解决 MDP 的另一种基于 MC 的方法是使用离策略控制，我们将在本秘籍中讨论。

off-policy方法使用另一个策略（称为行为策略b ）生成的数据优化目标策略π。目标策略始终执行开发，而行为策略用于探索目的。这意味着目标策略对其当前的 Q 函数是贪婪的，并且行为策略生成行为以便目标策略有数据可供学习。行为策略可以是任何东西，只要能以非零概率选择所有状态下的所有动作即可，这保证了行为策略可以探索所有可能性。

由于我们在 off-policy 方法中处理两个不同的策略，我们只能在两个策略中发生的情节中使用共同的步骤。这意味着我们从最新的一步开始，其在行为策略下采取的行动与在贪婪策略下采取的行动不同。为了了解另一个策略的目标策略，我们使用了一种称为重要性采样的技术，该技术通常用于在给定从不同分布生成的样本的情况下估计分布下的期望值。状态-动作对的加权重要性计算如下：

这里，π ( ak | sk ) 是目标策略下在状态sk采取动作ak的概率；b ( ak | sk ) 是行为策略下的概率；权重wt是从步骤t到事件结束的这两个概率之间的比率的乘积。权重wt应用于步骤t的回报。

怎么做...

让我们使用以下步骤来搜索具有 off-policy MC 控制的最优 Blackjack 策略：

1.导入必要的模块并创建一个 Blackjack 实例：

>>> import torch
>>> import gym
>>> env = gym.make('Blackjack-v0')

2.我们首先定义行为策略，在我们的案例中随机选择具有相同概率的动作：

>>> def gen_random_policy(n_action):
...     probs = torch.ones(n_action) / n_action
...     def policy_function(state):
...         return probs
...     return policy_function
>>> random_policy = gen_random_policy(env.action_space.n)

行为策略可以是任何东西，只要它以非零概率选择所有状态下的所有动作。

3.接下来，让我们开发一个运行情节并根据行为策略采取行动的功能：

>>> def run_episode(env, behavior_policy):
...     """
...     给定行为策略运行一集
...     @param env: OpenAI Gym 环境
...     @param behavior_policy: 行为策略
...     @return：整个剧集的结果状态、动作和奖励
...     """
...     state = env.reset()
...     rewards = []
...     actions = []
...     states = []
...     is_done = False
...     while not is_done:
...         probs = behavior_policy(state)
...         action = torch.multinomial(probs, 1).item()
...         actions.append(action)
...         states.append(state)
...         state, reward, is_done, info = env.step(action)
...         rewards.append(reward)
...         if is_done:
...             break
...     return states, actions, rewards

这记录了情节中所有步骤的状态、动作和奖励，这些将用作目标策略的学习数据。

4.现在，我们将开发 off-policy MC 控制算法：

>>> from collections import defaultdict
>>> def mc_control_off_policy(env, gamma, n_episode, behavior_policy):
...     """
...     使用off-policy MC控制方法获取最优策略
...     @param env: OpenAI健身房环境
...     @param n_episode：剧集数
...     @param behavior_policy：行为策略
...     @return：最优Q函数，以及最优策略
...     """
...     n_action = env.action_space.n
...     G_sum = defaultdict(float)
...     N = defaultdict(int)
...     Q = defaultdict(lambda: torch.empty(n_action))
...     for episode in range(n_episode):
...         W = {}
...         w = 1
...         states_t, actions_t, rewards_t = 
                     run_episode(env, behavior_policy)
...         return_t = 0
...         G = {}
...         for state_t, action_t, reward_t in zip(states_t[::-1], 
                                 actions_t[::-1], rewards_t[::-1]):
...             return_t = gamma * return_t + reward_t
...             G[(state_t, action_t)] = return_t
...             if action_t != torch.argmax(Q[state_t]).item():
...                 break
...             w *= 1./ behavior_policy(state_t)[action_t]
...         for state_action, return_t in G.items():
...             state, action = state_action
...             if state[0] <= 21:
...                 G_sum[state_action] += 
                                 return_t * W[state_action]
...                 N[state_action] += 1
...                 Q[state][action] = 
                             G_sum[state_action] / N[state_action]
...     policy = {}
...     for state, actions in Q.items():
...         policy[state] = torch.argmax(actions).item()
...     return Q, policy

5.我们将折扣率指定为 1，并将使用 500,000 集：

>>> gamma = 1
>>> n_episode = 500000

6.使用行为策略执行离策略 MC 控制random_policy以获得最优 Q 函数和策略：

>>> optimal_Q, optimal_policy = mc_control_off_policy(env, gamma, n_episode, random_policy)

这个怎么运作...

在这个秘籍中，我们用 off-policy MC 解决了 Blackjack 游戏。

在第 4 步中，off-policy MC 控制算法完成以下任务：

它用任意小值初始化 Q 函数。
它运行n_episode剧集。
对于每一集，它执行行为策略以生成状态、动作和奖励；它使用基于通用步骤的首次访问 MC 预测对目标策略进行策略评估；并根据加权回报更新 Q 函数。
最终确定最优Q-function，通过对最优Q-function中的每个状态采取最佳动作得到最优策略。

它通过观察另一个代理并重用从另一个策略生成的经验来了解目标策略。目标策略以贪婪的方式进行优化，而行为策略不断探索不同的选项。它将行为策略的回报与它们在目标策略中的概率的重要性比进行平均。您可能想知道为什么在计算重要性比wt时 π ( ak | sk ) 总是等于 1 。回想一下，我们只考虑在行为策略下采取的共同步骤，并且可能是目标策略，而目标策略总是贪婪的。因此，π ( a | s ) = 1 始终为真。

还有更多...

我们其实可以用增量的方式来实现MC方法。在一个情节中，我们可以动态计算 Q 函数，而不是存储每个首次出现的状态-动作对的回报率和重要性比率。以非增量方式，最后计算 Q 函数，其中包含 n 个情节中的所有存储回报：

而在增量方法中，Q 函数在 episode 的每个步骤中更新如下：

增量等效更有效，因为它减少了内存消耗并且更具可扩展性。让我们继续实施它：

>>> def mc_control_off_policy_incremental(env, gamma, n_episode, behavior_policy):
...     n_action = env.action_space.n
...     N = defaultdict(int)
...     Q = defaultdict(lambda: torch.empty(n_action))
...     for episode in range(n_episode):
...         W = 1.
...         states_t, actions_t, rewards_t = 
                             run_episode(env, behavior_policy)
...         return_t = 0.
...         for state_t, action_t, reward_t in 
                     zip(states_t[::-1], actions_t[::-1], rewards_t[::-1]):
...             return_t = gamma * return_t + reward_t
...             N[(state_t, action_t)] += 1
...             Q[state_t][action_t] += (W / N[(state_t, action_t)])
                                 * (return_t - Q[state_t][action_t])
...             if action_t != torch.argmax(Q[state_t]).item():
...                 break
...             W *= 1./ behavior_policy(state_t)[action_t]
...     policy = {}
...     for state, actions in Q.items():
...         policy[state] = torch.argmax(actions).item()
...     return Q, policy

我们可以调用这个增量版本来获得最优策略：

>>> optimal_Q, optimal_policy = mc_control_off_policy_incremental(env, gamma, n_episode, random_policy)

也可以看看

关于重要性采样的详细解释，下面是一个完美的资源：

https://statweb.stanford.edu/~owen/mc/Ch-var-is.pdf

使用加权重要性采样开发 MC 控制

在之前的秘籍中，我们简单地将行为策略的回报与它们在目标策略中的概率的重要性比进行了平均。这种技术正式称为普通重要性采样。众所周知，它具有高方差，因此，我们通常更喜欢重要性采样的加权版本，我们将在本节中讨论。

加权重要性抽样与普通重要性抽样的不同之处在于它平均回报的方式。它不是简单地平均，而是取收益的加权平均值：

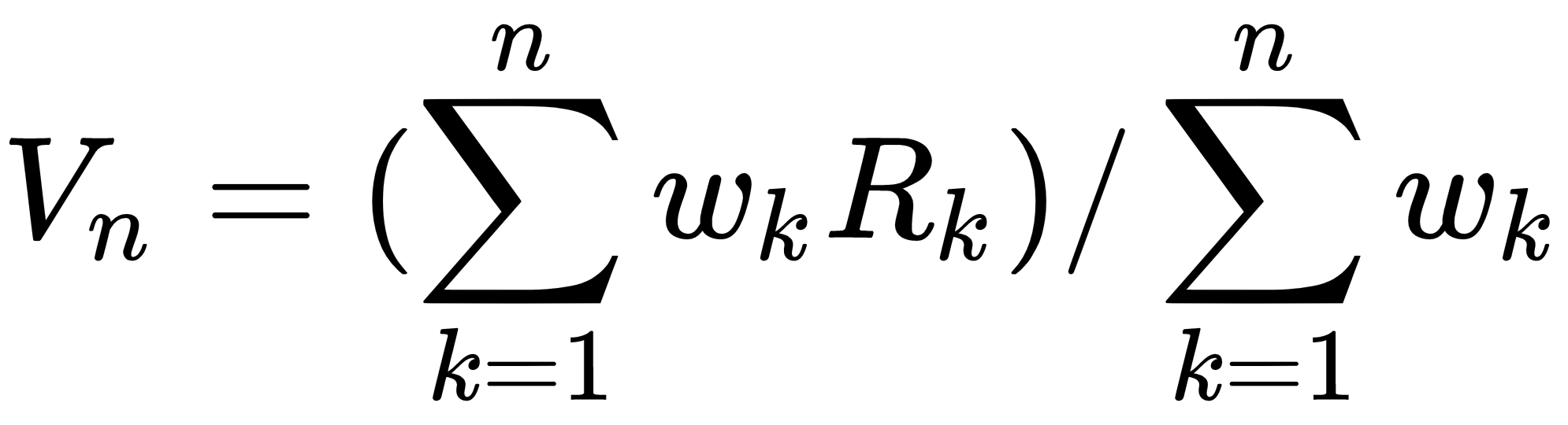
与普通版本相比，它的方差通常要低得多。如果你对 Blackjack 进行过普通的重要性抽样实验，你会发现每次实验的结果差异很大。

怎么做...

让我们通过使用以下步骤使用带有加权重要性采样的离策略 MC 控制来解决 Blackjack：

1.导入必要的模块并创建一个 Blackjack 实例：

>>> import torch
>>> import gym
>>> env = gym.make('Blackjack-v0')

2.我们首先定义行为策略，在我们的案例中随机选择具有相同概率的动作：

>>> random_policy = gen_random_policy(env.action_space.n)

3.接下来，我们重用该run_episode函数，它运行一个情节并根据行为策略采取行动。

4.现在，我们开发具有加权重要性采样的离策略 MC 控制算法：

>>> from collections import defaultdict
>>> def mc_control_off_policy_weighted(env, gamma, n_episode, behavior_policy):
...     """
...     带权重采样的off-policy MC控制方法获取最优策略
...     @ param env：OpenAI Gym 环境
...     @param gamma：折扣因子
...     @param n_episode：剧集数
...     @param behavior_policy：行为策略
...     @return：最优 Q 函数和最优策略
...     """
...     n_action = env.action_space.n
...     N = defaultdict(float)
...     Q = defaultdict(lambda: torch.empty(n_action))
...     for episode in range(n_episode):
...         W = 1.
...         states_t, actions_t, rewards_t = 
                             run_episode(env, behavior_policy)
...         return_t = 0.
...         for state_t, action_t, reward_t in zip(states_t[::-1], 
                                 actions_t[::-1], rewards_t[::-1]):
...             return_t = gamma * return_t + reward_t
...             N[(state_t, action_t)] += W
...             Q[state_t][action_t] += (W / N[(state_t, action_t)]) 
                                 * (return_t - Q[state_t][action_t])
...             if action_t != torch.argmax(Q[state_t]).item():
...                 break
...             W *= 1./ behavior_policy(state_t)[action_t]
...     policy = {}
...     for state, actions in Q.items():
...         policy[state] = torch.argmax(actions).item()
...     return Q, policy

请注意，这是 MC 控件的增量版本。

5.我们将折扣率指定为 1，并将使用 500,000 集：

>>> gamma = 1
>>> n_episode = 500000

6.使用行为策略执行离策略 MC 控制random_policy以获得最优 Q 函数和策略：

>>> optimal_Q, optimal_policy = mc_control_off_policy_weighted(env, gamma, n_episode, random_policy)

这个怎么运作...

在这个秘籍中，我们使用带有加权重要性采样的离策略 MC 控制解决了 Blackjack 问题。它与普通的重要性抽样非常相似，但它不是通过比率缩放回报并对结果求平均，而是使用加权平均值来衡量回报。而且，在实践中，加权重要性抽样的方差比普通重要性抽样低得多，因此更受青睐。

还有更多...

最后，我们为什么不模拟一些情节，看看在由此产生的最优策略下获胜和失败的机会是多少？

我们重用simulate_episode我们在Performing on-policy Monte Carlo 控制配方中开发的函数并模拟 100,000 集：

>>> n_episode = 100000
>>> n_win_optimal = 0
>>> n_lose_optimal = 0
>>> for _ in range(n_episode):
...     reward = simulate_episode(env, optimal_policy)
...     if reward == 1:
...         n_win_optimal += 1
...     elif reward == -1:
...         n_lose_optimal += 1

然后，我们打印出我们得到的结果：

>>> print('Winning probability under the optimal policy: {}'.format(n_win_optimal/n_episode))
Winning probability under the optimal policy: 0.43072
>>> print('Losing probability under the optimal policy: {}'.format(n_lose_optimal/n_episode))
Losing probability under the optimal policy: 0.47756

也可以看看

为了证明加权重要性抽样优于普通重要性抽样这一事实，请随时查看以下内容：

海斯特伯格，T . C.，重要性抽样的进展，博士。D. _ 论文，统计系，斯坦福大学，1988 年
卡塞拉，G .，罗伯特，C . P.， 后处理接受-拒绝样本：回收和重新缩放。计算和图形统计杂志, 7 ( 2 ): 139–157 , 1988
Precup , D. , Sutton , R. S. , Singh , S. ，政策外政策评估的资格追踪。第 17 届国际机器学习会议论文集，第 759 – 766页，2000 年