相关阅读

数字IC基础知识：著名EDA公司与工具介绍

---

        如果时序机的两个状态对于所有可能的输入序列都具有相同的输出序列（和相同的下一状态），则称这两个状态是等价的。时序机的等价状态无法通过观察输出序列的异同对其加以区分；合并等价状态也不会改变状态机的输入输出特性。通过识别合并等价状态也不会改变状态机的输入-输出特性。通过识别合并等价状态可以化简时序机的状态表与状态转移图，并且在无需综合考虑电路功能的情况下减少硬件开销（因为没必要对等价状态进行编码）。一般而言，对每一个有限状态机来说，都会存在至少一个唯一的最简等效状态机。

例 状态表如表1所示的状态机有两个等价状态：S_4与S_5。在输入信号的作用下，两个状态S_4和S_5具有相同的下一状态和输出。也就是说，当状态机处于状态S_4并有输入序列作用时，其输出与状态机处于S_5且在相同输入序列作用下时的输出是完全相同的。图1给出了该状态机的状态转移图，并说明了状态S_4与状态S_5如何映射到相同的下一状态；并且对所有的有效输入，这两个等价状态都具有相同的输出。

表1 等价状态S_4与S_5的下一状态表和输出表。

用S_4代替S_5，并将S_5所在行删除，以此来化简该表

	下一状态		输出
	输入		输入
当前状态	0	1	0	1
S_0	S_6	S_3	0	0
S_1	S_1	S_6	0	1
S_2	S_2	S_5（应使用S_4代替）	0	1
S_3	S_7	S_3	0	1
S_4	S_7	S_2	0	0
S_5（删除该行）	S_7	S_2	0	0
S_6	S_0	S_1	0	0
S_7	S_4	S_3	0	0

图1 等价状态的状态转移图

        如果时序机状态表中与两个状态有关的行是相同的，则称这两个状态是等价的。删除一个等价状态外的其余全部等价状态，并使受此影响的弧线重新指向保留的最后一个等级状态，就会使状态转移图得到简化。但是需要注意，当两个状态在状态表中相应的行不同时，也不要轻易得出这两个状态不是等价状态的结论，下一状态表中完全相同行的条件仅是其对应状态等价的充分条件，而不是必要条件。因此，仅仅比较状态表中的行并不是判别等价状态的充分方法，还存在这种方法可能检测不到的其他等价状态。

        删除等价状态更一般的方法依赖于如下的等价递归定义：如果两个状态对各输入值具有相同的输出，并且对同样的输入值，它们所转移到的下一状态也是相同（或等价）的，则这两个状态是等价的。删除等价状态的步骤可归纳为：（1）画出一个三角形的表格（参见表2）来表示不同状态的可能组合对；（2）分析组合对状态的等价条件（由原状态表已经知道S_4与S_5是等价的，所以这里就不再考虑S_5了）。再来看一个例子，如果S_0与S_4转移到的下一状态是等价的，并且它们对各个可能的输入所对应的输出也是相同的，则认为S_0和S_4是等价状态。图1所示的状态表中，S_0与S_4具有相同的输出，但只有当S_6与S_7等价并且S_2与S_3等价这两个条件同时满足时，S_0与S_4才是等价的。

表2 表示可能等价状态对的表格

S_1	不可能
S_2	不可能	S_6和S_4
S_3	不可能	S_1和S_7、S_6和S_3	S_2和S_7、S_4和S_3
S_4	S_6和S_7、S_3和S_2	不可能	不可能	不可能
S_6	S_3和S_1	不可能	不可能	不可能	S_7和S_0、S_2和S_1
S_7	S_6和S_4	不可能	不可能	不可能	S_2和S_3	S_0和S_4、S_1和S_3
	S_0	S_1	S_2	S_3	S_4	S_6

        在表格的对应行列中，列出了行列所对应的一对状态的等价条件。例如，当状态机处于状态S_1时，如果输入0或1，其下一状态分别为S_1或S_6；同样，当状态机处于S_3时，在上述相同输入的作用下，它的下一状态分别为S_7与S_3。因此，S_1与S_3等价的充要条件是：S_1与S_7等价，且S_6与S_3等价（当然此时他们在相同输出时的输出要是一样的，如果这个违反了，就会被标记为不可能）。

        在所有可能等价的状态中，我们从表中可以发现S_1与S_3不等价，因为S_1与S_7在表中被标记为不可能等价，S_2与S_3也不等价，因为S_2与S_7在表中被标记为不可能等价。在探讨S_7与S_0的等价关系时，我们会遇到一些问题，S_7与S_0等价要求S_6和S_4等价，S_6和S_4等价要求S_7和S_0、S_2和S_1都等价，而S_2和S_1等价又要求S_6和S_4等价，我们会发现其中存在许多循环等价，即A能证明B，B能证明A，这并不能判断A、B是否为真。但是我们的原则是，无矛盾，则接受。如果我们认为S_7与S_0、S_6和S_4、S_2和S_1分别等价，且这并不会产生矛盾，能逻辑自洽，则就这么做，因为这样能减少状态机的状态数。

        最后可以得到图2所示的简化状态转移图，只包含了4个状态，而非8个。

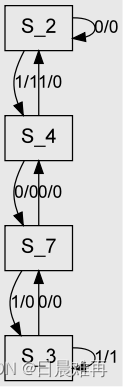
 图2 完全化简的状态转移图

以上内容来源于《Verilog HDL高级数字设计》