数据结构–树的定义与基本术语

数的基本概念

树:从树根生长，逐级分支

$非空树$的特性:
有且仅有一个根节点
没有后继的结点称为“叶子结点”(或终端结点)
有后继的结点称为“分支结点”(或非终端结点)
除了根节点外，任何一个结点都有且仅有一个前驱
每个结点可以有0个或多个后继。

$除了根节点外，任何一个结点都有且仅有一个前驱$

树的数学定义
树是n (n>0）个结点的有限集合，n=0 时，称为空树，这是一种特殊情况。在任意一棵非空树中应满足:

1. 有且仅有一个特定的称为$根$的结点。
2. 当n >1时，其余结点可分为 m (m>0) 个$互不相交的有限集合$$T_1,T_2,...,T_m$，其中每个集合本身又是一棵树，并且称为根结点的$子树$。

$树是一种递归定义的数据结构$

树形逻辑结构的应用

结点之间的关系描述

祖先结点：

在树结构中，一个节点的祖先节点是指其在树中的上层节点，沿着树的路径从根节点到该节点的所有节点都是它的祖先节点。换句话说，一个节点的祖先节点包括其父节点、爷爷节点、曾祖父节点等等，一直追溯到树的根节点。

子孙结点：

在树结构中，一个节点的子孙节点是指其在树中的下层节点，沿着树的路径从该节点到叶子节点的所有节点都是它的子孙节点。换句话说，一个节点的子孙节点包括其子节点、孙子节点、曾孙节点等等，一直追溯到树的叶子节点。

双亲结点：

双亲结点是指在树或者图中，某个节点的直接前驱节点。在树中，每个节点除了根节点外，都有一个直接前驱节点，称为双亲结点。双亲结点是通过指向该节点的指针或引用来访问的。

孩子结点：

孩子结点是指在树或者图中，某个节点的直接后继节点。在树中，每个节点可以有零个或多个孩子结点。孩子结点是通过被该节点指针或引用所指向的节点来访问的。一个节点的孩子结点可以是多个，但是孩子结点只有一个双亲结点。

兄弟结点：

兄弟结点是指在树或者图中，具有相同双亲结点的节点之间的关系。换句话说，兄弟节点是指具有相同父节点的节点。兄弟节点之间没有直接的连接，它们是通过共同的双亲结点来关联的。在树结构中，兄弟节点是在同一层级上的节点。兄弟节点之间的顺序通常是由它们在父节点中的位置确定的。

堂兄弟结点：

堂兄弟节点是指在家族关系树中，具有相同祖父节点但是双亲结点不同的节点之间的关系。换句话说，堂兄弟节点是指在同一代中，双亲是兄弟姐妹的节点。堂兄弟节点之间没有直接的连接，它们是通过共同的祖父节点来关联的。堂兄弟节点之间的关系比较远，亲缘关系相对较弱。

两个结点之间的路径

在树中，两个节点之间的距离是指从一个节点到达另一个节点所经过的边的数量

$只能从上往下$

什么是路径长度

在树中，路径长度是指从一个节点到达另一个节点所经过的边的个数

结点、树的属性描述

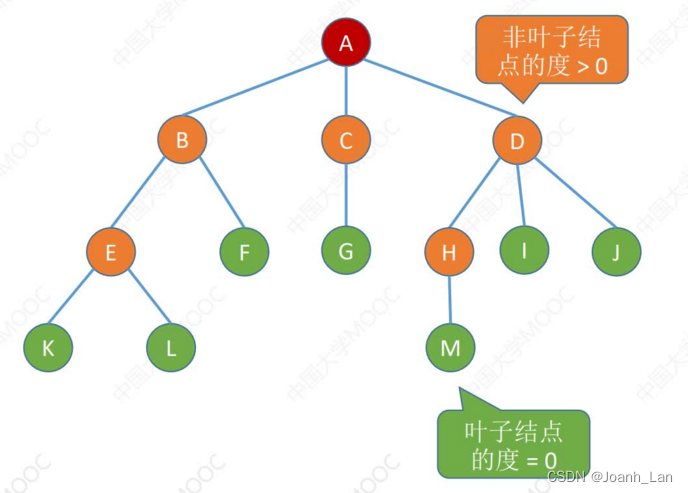
属性:
结点的层次（深度）―一从上往下数
$默认从1开始$
结点的高度――从下往上数
树的高度（深度）―—总共多少层
$结点的度$――有几个孩子(分支)
$树的度$—―各结点的度的最大值

有序树v.S无序树

有序树――逻辑上看，树中结点的各子树从左至右是$有次序$的，不能互换

无序树――逻辑上看，树中结点的各子树从左至右是$\color{red}无次序$的，可以互换

$具体看你用树存什么，是否需要用结点的左右位置反映某些逻辑关系$

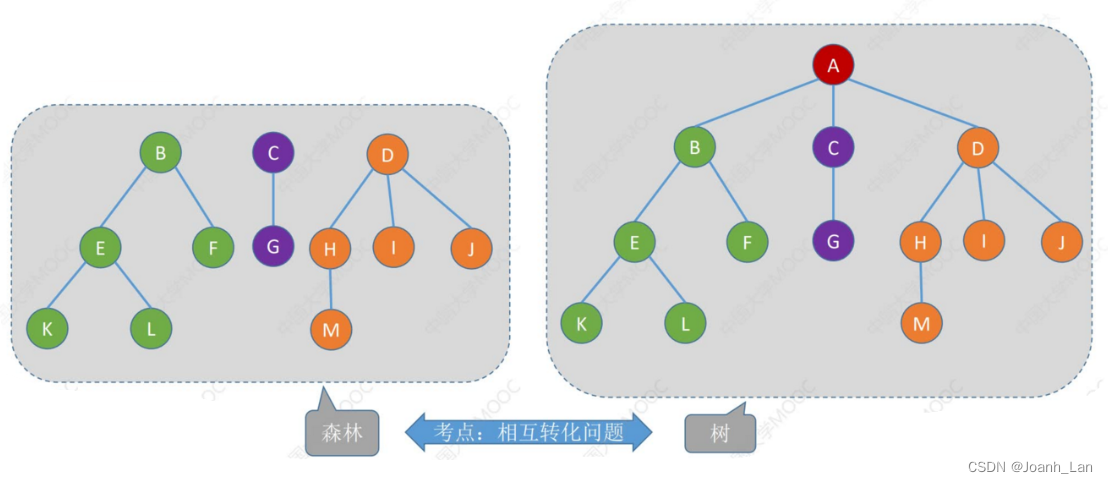
树v.S森林

森林。森林是m (m≥0）棵互不相交的树的集合

$m可为0空森林$

Eg:全中国所有人家的家谱

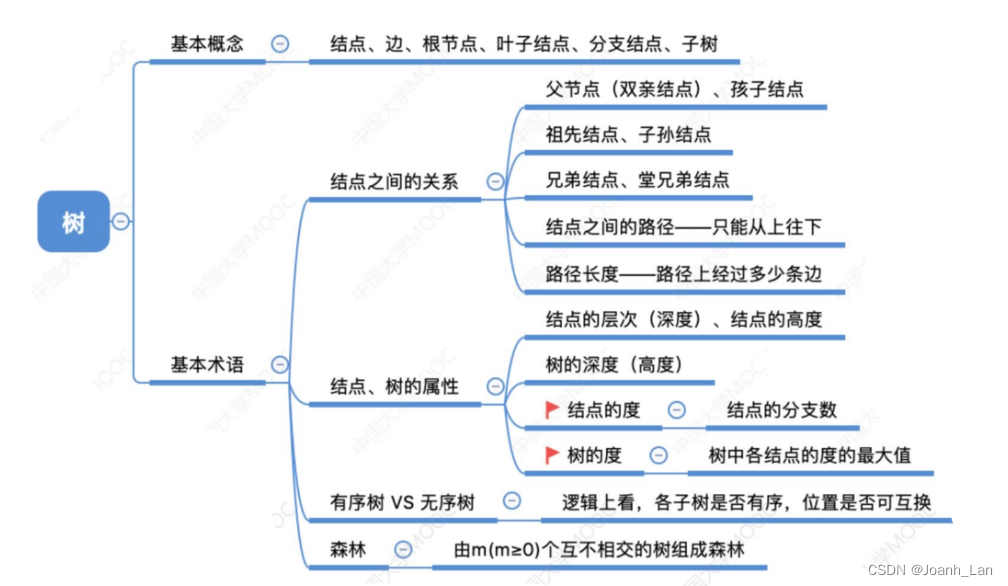
知识点回顾与重要考点