今日题目

[NOIP1998 提高组] 车站

题目描述

火车从始发站（称为第 $1$ 站）开出，在始发站上车的人数为 $a$，然后到达第 $2$ 站，在第 $2$ 站有人上、下车，但上、下车的人数相同，因此在第 $2$ 站开出时（即在到达第 $3$ 站之前）车上的人数保持为 $a$ 人。从第 $3$ 站起（包括第 $3$ 站）上、下车的人数有一定规律：上车的人数都是前两站上车人数之和，而下车人数等于上一站上车人数，一直到终点站的前一站（第 $(n-1)$ 站），都满足此规律。现给出的条件是：共有 $n$ 个车站，始发站上车的人数为 $a$ ，最后一站下车的人数是 $m$（全部下车）。试问 $x$ 站开出时车上的人数是多少？

输入格式

输入只有一行四个整数，分别表示始发站上车人数 $a$，车站数 $n$，终点站下车人数 $m$ 和所求的站点编号 $x$。

输出格式

输出一行一个整数表示答案：从 $x$ 站开出时车上的人数。

样例 #1

样例输入 #1

5 7 32 4

样例输出 #1

13

提示

对于全部的测试点，保证 $1\le a\le 20$，$1\le x\le n\le 20$，$1\le m\le 2\times 10^4$。

解题思路

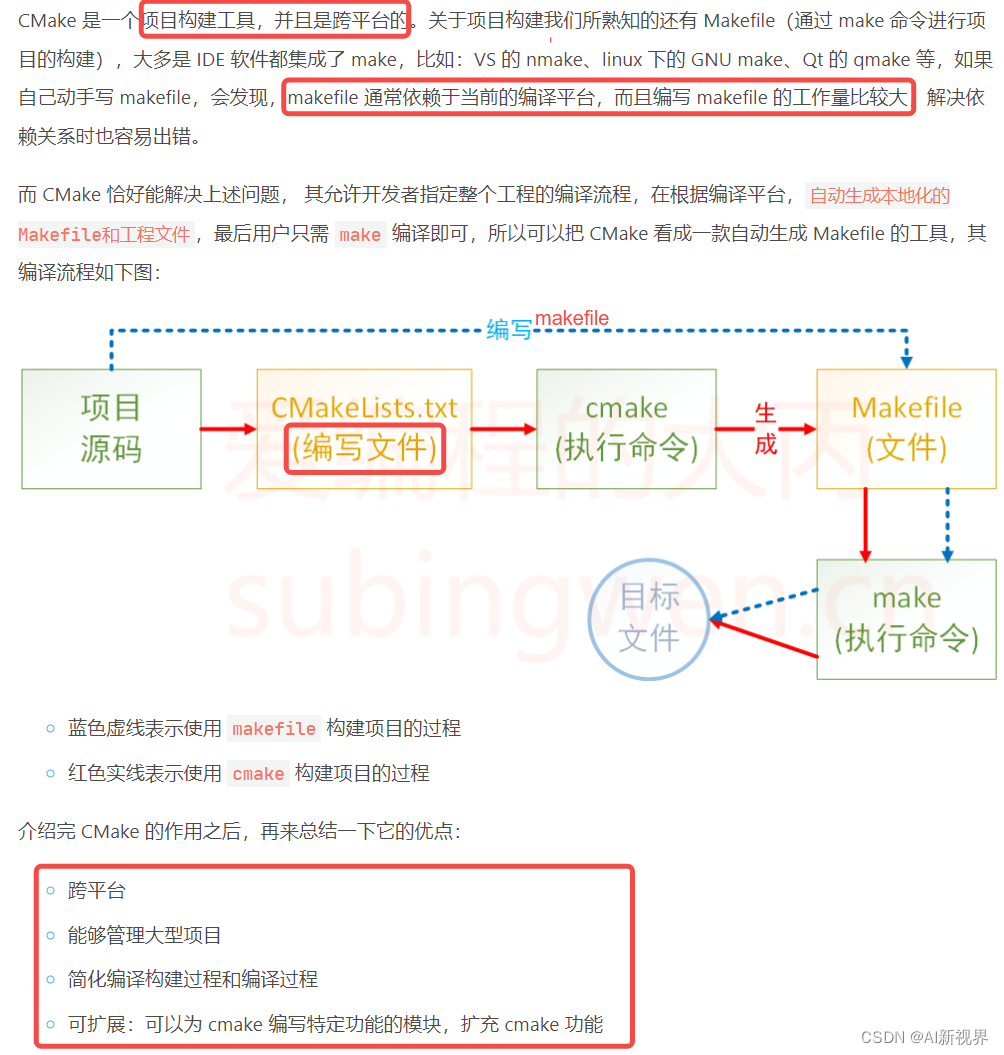
手推找规律，演草纸图片如下，其中涉及斐波那契数列，用 $f(x)$ 表示

找到了 当 $n⩾4$ 时 ，$n$ 和 $m$ 的关系：
第 $n$ 站后车上的人数 $m$ 的表示如下
$$m=(2+h[n-4])\ast a+h[n-3]\ast mul$$（其中 $h[t]$ 表示斐波那契数列前 $t$ 项和，$mul$ 表示倍数）
剩下的就是简单的数列问题了。
其他的小细节要注意处理。

代码实现

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
int f[30],h[30],p[30]; 
int a,n,m,x,ans;
void checkx(int mul){
	if(x>=4) ans=(2+h[x-4])*a+h[x-3]*mul;
	else if(x==1||x==2) ans=a;
	else if(x==3) ans=2*a;
}
int main()
{
	f[1]=1; f[2]=1;
	h[1]=1; h[2]=2;
	for(int i=3;i<=25;i++)
	{
		f[i]=f[i-1]+f[i-2];
		h[i]=h[i-1]+f[i];
	}
	
	cin>>a>>n>>m>>x;
	if(n>=5){
		int mul=0;
		mul=(m-(2+h[n-5])*a)/h[n-4];
		checkx(mul);
	}
	else checkx(0);
	cout<<ans<<endl;
	return 0;
}  

反思总结

做这种数学题的时候多找找数学规律，节约时间空间，代码量小，简单快捷。