文章目录
- 一.红黑树的定义
- 红黑树平衡性论证
- 二.红黑树的节点插入
- 插入新节点后最小违规子结构(抽象分析)
- 最小违规子结构一号的规则化算法分析
- 最小违规子结构二号的规则化算法分析
- 三.红黑树类代码托管
- 四.红黑树与AVL树的对比
旷世奇才发明的数据结构
一.红黑树的定义
- 红黑树的节点定义:
enum Colour
{
RED,
BLACK,
};
template<class KEY,class VALUE>
struct RBTreeNode
{
RBTreeNode<KEY,VALUE>* _left;
RBTreeNode<KEY, VALUE>* _right;
RBTreeNode<KEY, VALUE>* _parent;
//KEY_VALUE键值对
pair<KEY, VALUE> _Key_Value;
//节点的颜色
Colour _color;
//默认构造红色节点
RBTreeNode(const pair<KEY, VALUE>& KEY_VALUE)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _Key_Value(KEY_VALUE)
, _color(RED)
{}
};
-
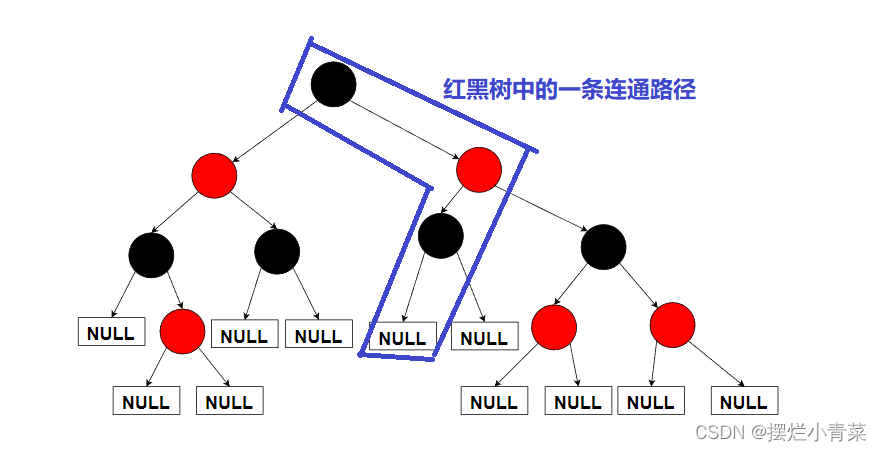
红黑树(或者其子结构)中的连通路径:红黑树(或者其子结构)中的连通路径指的是红黑树的根到空节点的路径,比如:
-
红黑树数据结构定义:红黑树满足二叉搜索树的所有性质
- (1).红黑树的所有节点被标记为红色或黑色
- (2).整颗红黑树的根节点必须为黑色
- (3).红黑树中的红色节点的左右孩子不能是红色节点(即在连通路径上红色节点不能连续出现)
- (4).红黑树的所有连通路径上的黑色节点数量必须相同
-
红黑树的路径特征值:
- 红黑树的规则(4)保证了红黑树及其任何一个子结构都分别有一个唯一的路径特征值,该特征值记录了红黑树(或其子结构)的连通路径上黑色节点的数量,规则(3)和规则(4)是红黑树平衡性的保证
红黑树平衡性论证
-
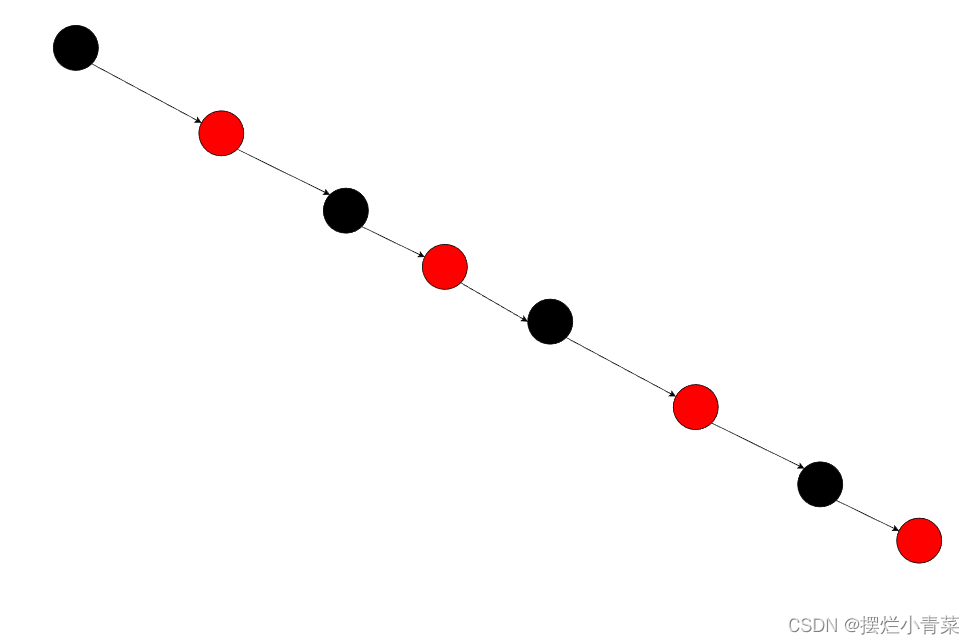
平衡性结论1:根据红黑树的定义,设整颗红黑树最长连通路径上节点总个数为X,整颗红黑树最短连通路径上节点总个数为Y,则有 X ≤ 2 Y X\leq2Y X≤2Y
- 论证结论1:设红黑树的路径特征值为Z,在最长连通路径上只能间隔地在Z个黑色节点间插入红色节点,因此最长连通路径的路径长度最大为2*Z;最短连通路径上可以不存在红色节点,因此最短连通路径的路径长度最小为Z;从而结论1得证:
X
≤
2
Z
≤
2
Y
X\leq2Z\leq2Y
X≤2Z≤2Y
- 论证结论1:设红黑树的路径特征值为Z,在最长连通路径上只能间隔地在Z个黑色节点间插入红色节点,因此最长连通路径的路径长度最大为2*Z;最短连通路径上可以不存在红色节点,因此最短连通路径的路径长度最小为Z;从而结论1得证:
X
≤
2
Z
≤
2
Y
X\leq2Z\leq2Y
X≤2Z≤2Y
-
平衡性结论2:根据平衡性结论1,当一颗红黑树的节点个数为N时,红黑树的高度H满足: H ≤ 2 l o g 2 N H\leq 2log_2N H≤2log2N
- 可以在满树的基础上改变节点分布证明平衡性结论2
-
综上,红黑树具有较好的平衡性,可以实现数据的高速检索.
-
相比于AVL树,红黑树要更抽象一些,它是根据自身的定义间接地控制树的高度从而保证平衡性
二.红黑树的节点插入
-
空树和只有一个黑色节点的树都满足红黑树的性质.
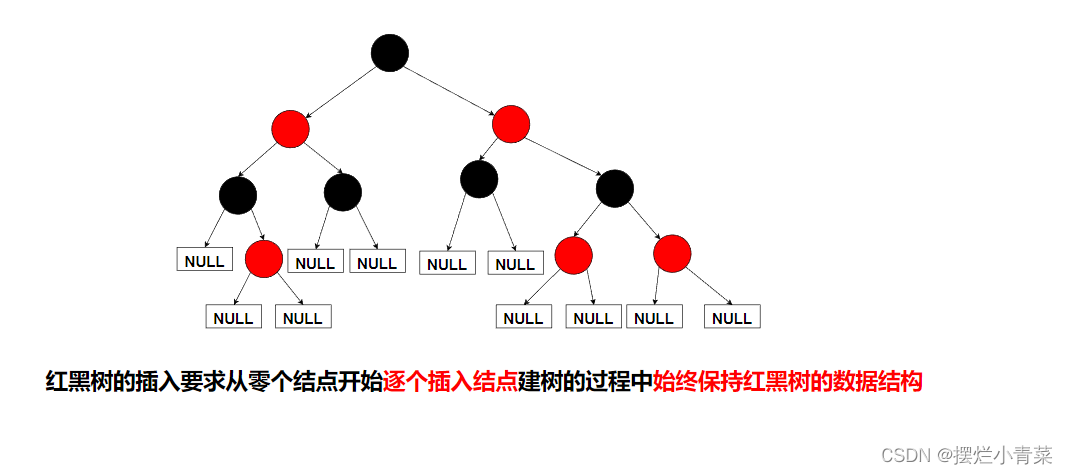
-
第一步先根据二叉搜索树的节点插入方式在红黑树的叶子节点位置插入新节点,比如:
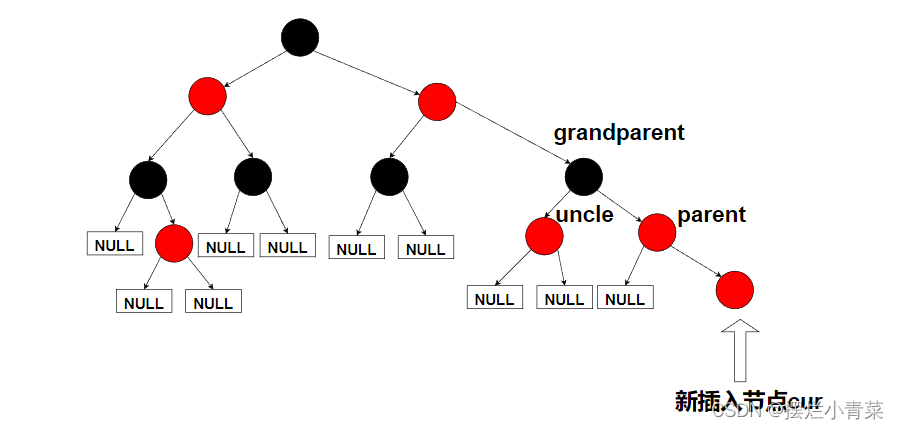
-
红黑树的插入操作只插入红色节点(插入黑色节点会导致路径特征值改变,不方便数据结构的调整)
bool insert(const Pair& KEYVALUE)
{
if (_root == nullptr)
{
_root = new Node(KEYVALUE);
_root->_color = BLACK;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
//查找插入的位置
while (cur != nullptr)
{
if (cur->_Key_Value.first < KEYVALUE.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_Key_Value.first > KEYVALUE.first)
{
parent = cur;
cur = cur->_left;
}
else
{
//KEY值重复,无法插入
return false;
}
}
//找到空位置执行插入
cur = new Node(KEYVALUE);
cur->_color = RED;
if (parent->_Key_Value.first < KEYVALUE.first)
{
//向右孩子插入
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
}
插入新节点后最小违规子结构(抽象分析)
- 要想设计数据结构的调整算法,就必须先抽象出要调整的结构对象
- 调整算法中会用到旋转算法,旋转平衡化参见: 旋转平衡化
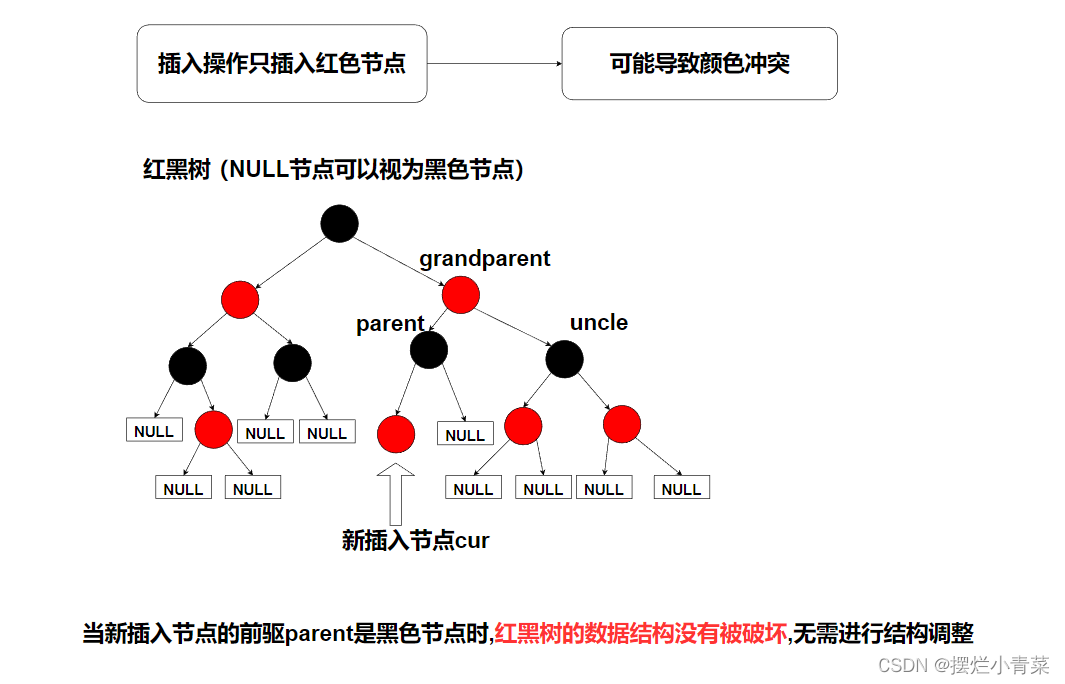
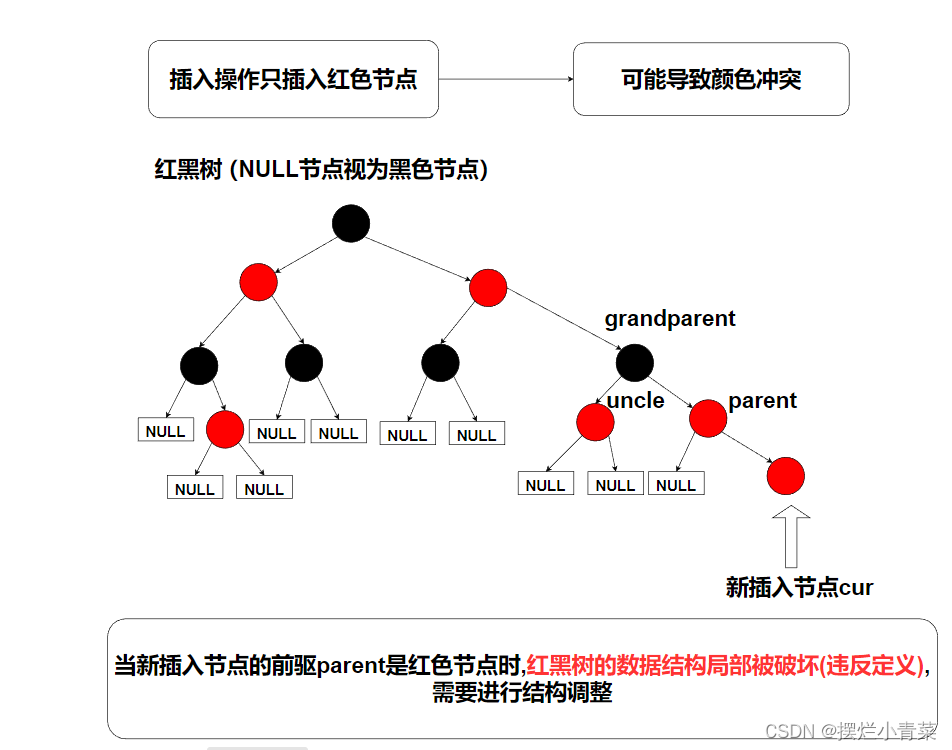
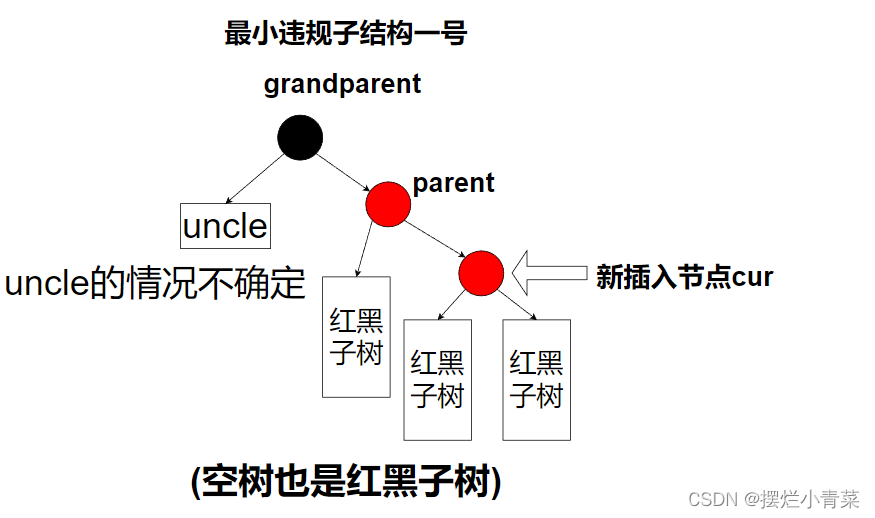
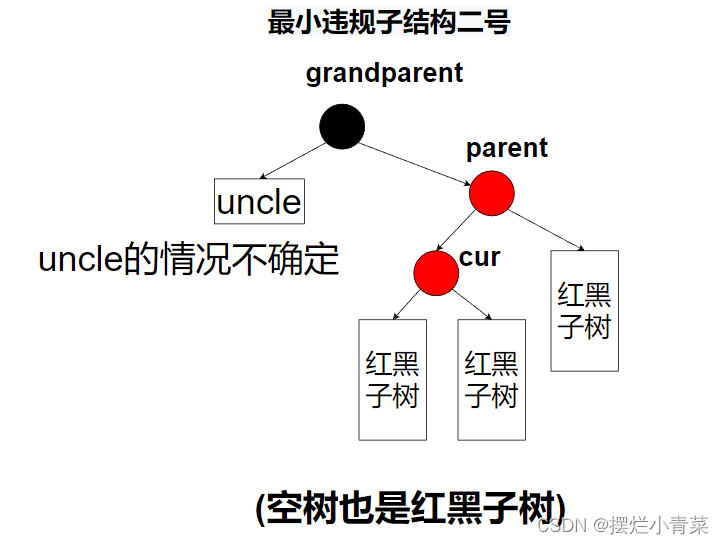
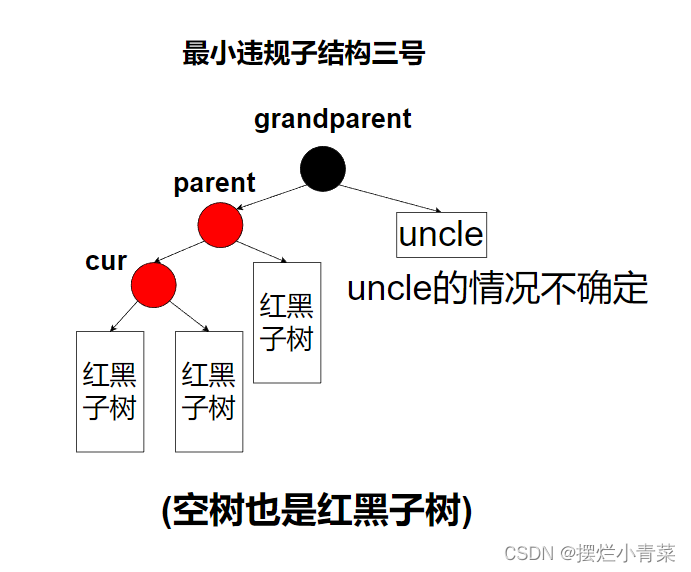
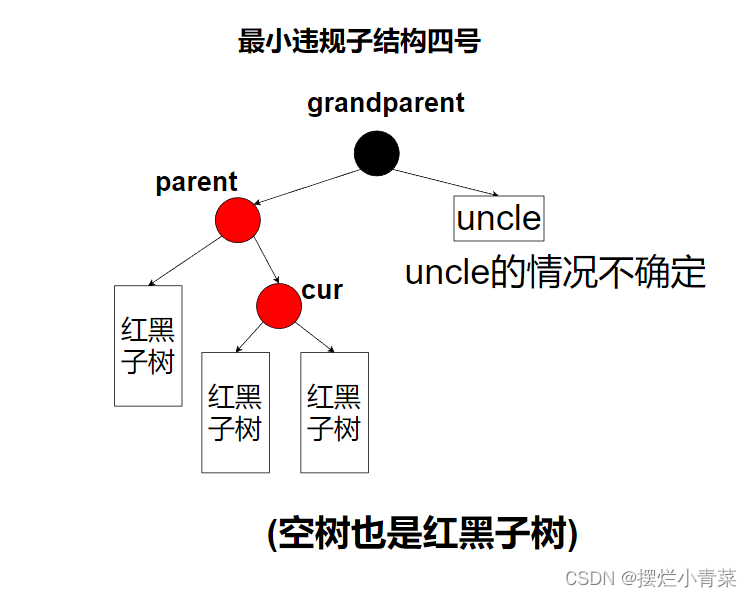
- 当新插入节点cur的前驱parent为红色时,红黑树局部违规,由于红黑树的根一定是黑色的,因此新节点cur的前驱parent一定不是整棵树的根,于是parent一定存在前驱grandparent,grandparent的另一个孩子我们称为uncle(uncle与parent同层,变色操作要求保持同层节点同一性,因此我们需要关注uncle).
- 前述的分析中,我们一共在违规结构中具象化出了四个节点(其中uncle存在与否及其颜色我们是不确定的),将与这四个节点相连的其他子结构抽象化,就可以得到下面四种最小违规子结构.
- 最小违规子结构一号:
- 最小违规子结构二号:
- 最小违规子结构三号:
- 最小违规子结构四号:
- 最小违规子结构一号:
- 最小违规子结构一号和二号分别与三号和四号是对称的,因此:
一号与三号的处理方式是相同的(只是旋转方向不同)
二号和四号的处理方式是相同的(只是旋转方向不同) - 对最小违规子结构的处理要保证如下几点要求:
- 1.维持二叉搜索树的性质
- 2.最小违规子结构中各个连通路径(从根到空节点)上的黑色节点数量不发生改变
- 3.消除节点之间的颜色冲突
最小违规子结构一号的规则化算法分析
-
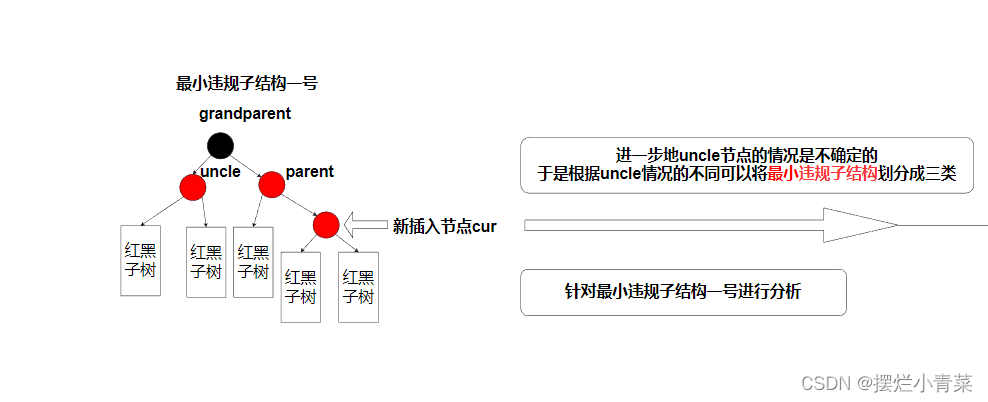
根据uncle的情况的不同可以将最小违规子结构进一步分为三种子情形进行处理:
- uncle节点存在且为红色
- uncle节点存在且为黑色或uncle为空节点
-
调整算法整体图解:

-
分块展示:
-
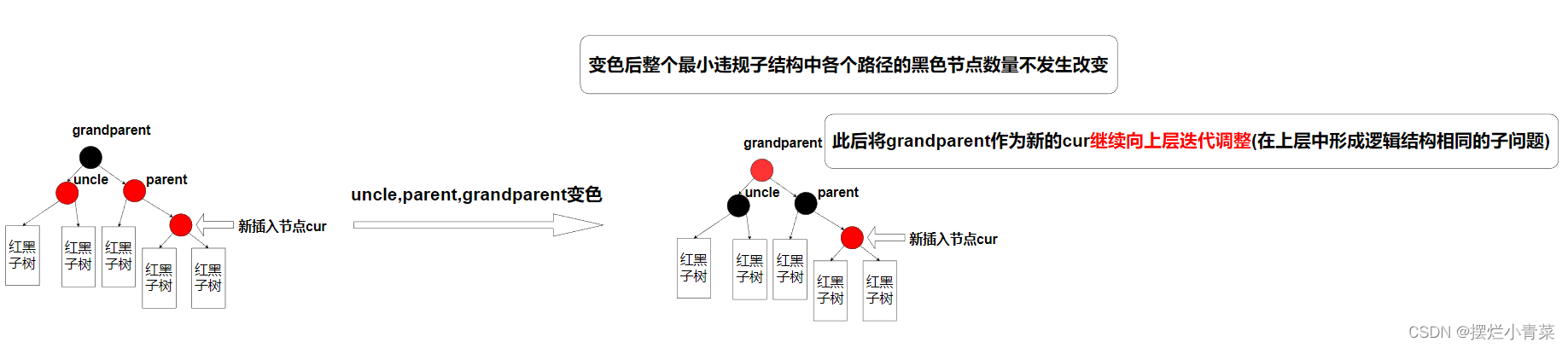
uncle节点存在且为红色:变色规则化
-
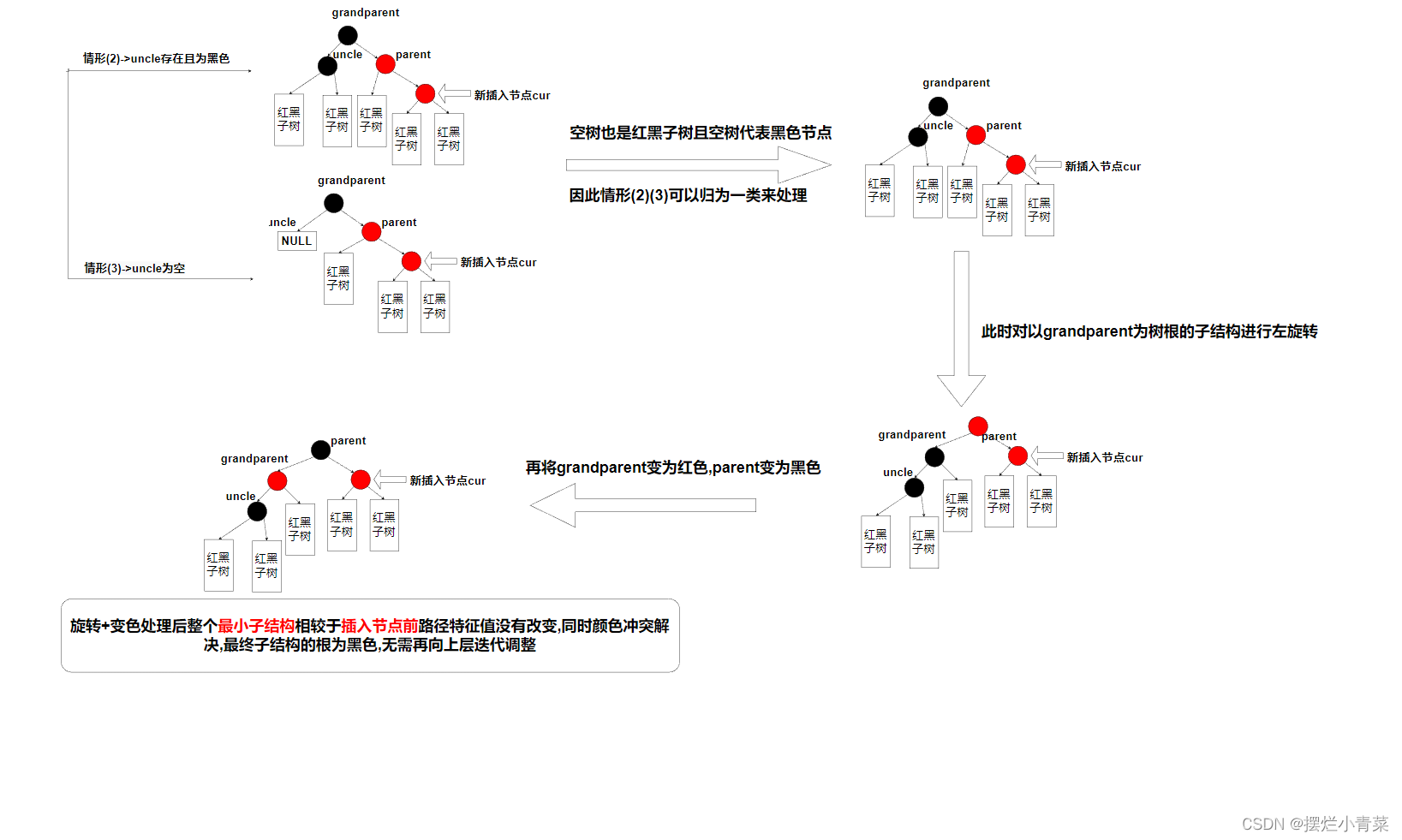
uncle节点存在且为黑色或uncle为空节点:单旋+变色规则化
-
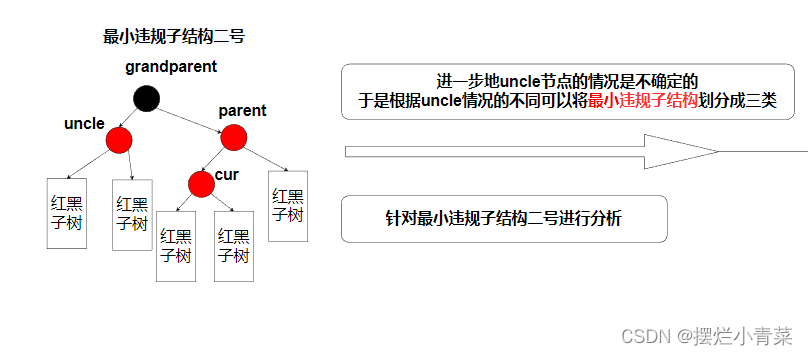
最小违规子结构二号的规则化算法分析
-
根据uncle的情况的不同可以将最小违规子结构进一步分为三种子情形进行处理:
- uncle节点存在且为红色
- uncle节点存在且为黑色或uncle为空节点
-
调整算法整体图解:

-
分块展示:
-
uncle节点存在且为红色:变色规则化

-
uncle节点存在且为黑色或uncle为空节点:双旋+变色规则化
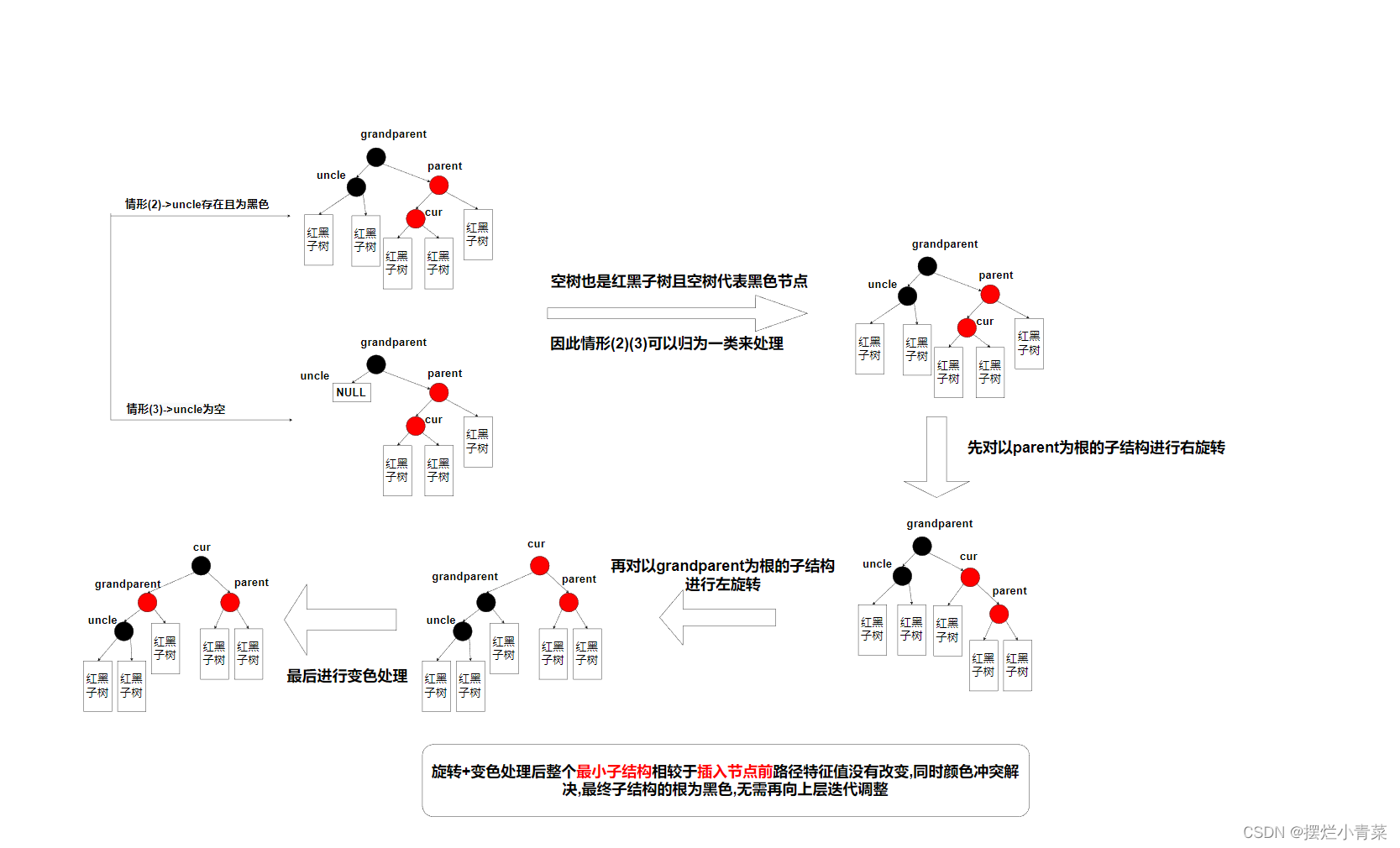
-
-
最小违规子结构三号和四号处理方式分别与一号和二号相同(只是旋转方向不同)
三.红黑树类代码托管
enum Colour
{
RED,
BLACK,
};
template<class KEY,class VALUE>
struct RBTreeNode
{
RBTreeNode<KEY,VALUE>* _left;
RBTreeNode<KEY, VALUE>* _right;
RBTreeNode<KEY, VALUE>* _parent;
//KEY_VALUE键值对
pair<KEY, VALUE> _Key_Value;
//节点的颜色
Colour _color;
//默认构造红色节点
RBTreeNode(const pair<KEY, VALUE>& KEY_VALUE)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _Key_Value(KEY_VALUE)
, _color(RED)
{}
};
template<class KEY, class VALUE>
class RBTree
{
typedef RBTreeNode<KEY, VALUE> Node;
typedef pair<KEY, VALUE> Pair;
public:
RBTree<KEY, VALUE>()
{
_root = nullptr;
}
//红黑树插入
bool insert(const Pair& KEYVALUE)
{
if (_root == nullptr)
{
_root = new Node(KEYVALUE);
_root->_color = BLACK;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
//查找插入的位置
while (cur != nullptr)
{
if (cur->_Key_Value.first < KEYVALUE.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_Key_Value.first > KEYVALUE.first)
{
parent = cur;
cur = cur->_left;
}
else
{
//KEY值重复,无法插入
return false;
}
}
//找到空位置执行插入
cur = new Node(KEYVALUE);
cur->_color = RED;
if (parent->_Key_Value.first < KEYVALUE.first)
{
//向右孩子插入
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
//如果cur的前驱parent是红色节点则我们需要对违规子结构进行迭代调整
while (parent && parent->_color == RED)
{
Node * grandparent = parent->_parent;
//区分最小违规子结构一二和三四号
if (grandparent->_right == parent)
{
Node* uncle = grandparent->_left;
//如果uncle为红色则按照情形(1)变色处理
if (uncle && uncle->_color == RED)
{
uncle->_color = BLACK;
parent->_color = BLACK;
grandparent->_color = RED;
//变色后将grandparent作为新的cur向上层迭代调整(最小违规子结构的逻辑形式不变)
cur = grandparent;
parent = cur->_parent;
}
//情形(2)-->先区分最小违规子结构一号和二号
else if (parent->_right == cur)
{
//一号最小违规子结构-->左单旋+变色
_RotationSL(grandparent);
grandparent->_color = RED;
parent->_color = BLACK;
//子结构的根变为黑色,无需再向上层继续迭代调整
break;
}
else
{
//二号最小违规子结构-->右左双旋+变色
_RotationSR(parent);
_RotationSL(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
//子结构的根变为黑色,无需再向上层继续迭代调整
break;
}
}
else
{
Node* uncle = grandparent->_right;
//如果uncle为红色则按照情形(1)变色处理
if (uncle && uncle->_color == RED)
{
uncle->_color = BLACK;
parent->_color = BLACK;
grandparent->_color = RED;
//变色后将grandparent作为新的cur向上层迭代调整(最小违规子结构的逻辑形式不变)
cur = grandparent;
parent = cur->_parent;
}
//情形(2)-->先区分最小违规子结构三号和四号
else if (parent->_left == cur)
{
//三号最小违规子结构-->右单旋+变色
_RotationSR(grandparent);
grandparent->_color = RED;
parent->_color = BLACK;
//子结构的根变为黑色,无需再向上层继续迭代调整
break;
}
else
{
//四号最小违规子结构-->左右双旋+变色
_RotationSL(parent);
_RotationSR(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
//子结构的根变为黑色,无需再向上层继续迭代调整
break;
}
}
}
//根据红黑树性质将根节点调整为黑色
_root->_color = BLACK;
return true;
}
//中序遍历
void Inorder()
{
_Inorder(_root);
std::cout << std :: endl;
}
void _CheckStruct()
{
//求路径特征值
int Benchmark = 0;
Node* tem = _root;
while (tem)
{
if (tem->_color == BLACK)
{
Benchmark++;
}
tem = tem->_left;
}
if (_CheckStruct(_root, 0, Benchmark))
{
std::cout << "StructureLegal" << std::endl;
}
}
private:
//左单旋成员接口
void _RotationSL(Node* parent)
{
//整个子结构的祖先(可能为空,即parent就是整棵树的树根)
Node* Graparent = parent->_parent;
Node* parentR = parent->_right;
//parentR的左子树(可能为空)
Node* parentRLSon = parentR->_left;
//左单旋
parent->_right = parentRLSon;
//注意parentLSon可能为空
if (parentRLSon)
{
parentRLSon->_parent = parent;
}
parentR->_left = parent;
parent->_parent = parentR;
//注意GGraparent可能为空
if (Graparent)
{
if (Graparent->_left == parent)
{
Graparent->_left = parentR;
}
else
{
Graparent->_right = parentR;
}
}
else
{
_root = parentR;
}
parentR->_parent = Graparent;
}
//右单旋成员接口
void _RotationSR(Node* parent)
{
Node* Graparent = parent->_parent;
Node* parentL = parent->_left;
Node* parentLRSon = parentL->_right;
//右单旋
parent->_left = parentLRSon;
if (parentLRSon)
{
parentLRSon->_parent = parent;
}
parentL->_right = parent;
parent->_parent = parentL;
if (Graparent)
{
if (Graparent->_left == parent)
{
Graparent->_left = parentL;
}
else
{
Graparent->_right = parentL;
}
}
else
{
_root = parentL;
}
parentL->_parent = Graparent;
}
//中序遍历搜索树
void _Inorder(Node * root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
std::cout << root->_Key_Value.first << ' ';
_Inorder(root->_right);
}
//检查红黑树结构的合法性
bool _CheckStruct(Node* root,int BlackNum,const int& benchmark)
{
if (root == nullptr)
{
//检查各路径的黑色节点数量是否相同
if (BlackNum == benchmark)
{
std::cout << "BlackNum:" << BlackNum << std::endl;
return true;
}
else
{
return false;
}
}
else if (root->_color == BLACK)
{
BlackNum++;
}
else if (root->_color == RED)
{
//检查红色节点在某条路径上是否连续出现
if (root->_parent && root->_parent->_color == RED)
{
return false;
}
}
return _CheckStruct(root->_left, BlackNum, benchmark) && _CheckStruct(root->_right, BlackNum, benchmark);
}
private:
Node* _root;
};
四.红黑树与AVL树的对比
- AVL树是严格平衡的搜索二叉树,由于AVL树的平衡性要求很高,因此面对大量的数据时,建树和删树的过程中很有可能会引发大量的旋转操作,从而导致性能下降,而红黑树是一种相对平衡的搜索二叉树,面对大量的数据时,建树和删树的过程中引发的旋转操作次数相对较少,在性能实测中,红黑树效率更胜一筹,从而在各种语言的库以及Linux内核中被频繁使用.







![NSS [SWPUCTF 2021 新生赛]no_wakeup](https://img-blog.csdnimg.cn/img_convert/0795a515de32c884f6536a9cb0981834.png)