后继节点定义：
二叉树以中序的方式进行遍历打印，节点X的下一个节点，就是X的后继节点。
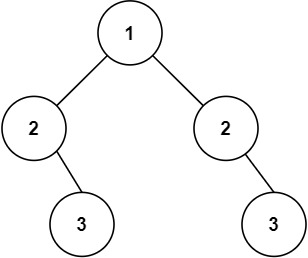
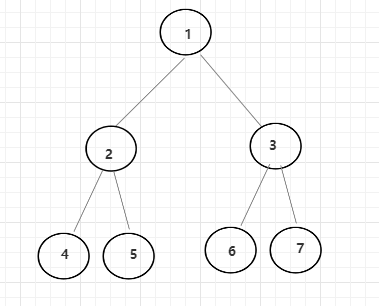
假设二叉树如下图所示：则中序遍历的后打印出来的就是 4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7。如果X = 3，则X的后继节点就是7。

如果Node的结构中只有left和right的话，那时间复杂度就是$O(N)$，从给定的头结点开始遍历，先打印出来中序，在遍历中序找到X，在找到X的下一个。
如果给定的Node的数据结构中包含parent指针，则可以将时间复杂度降低到$O(K)$。K为X到后继节点的实际距离。

public static class Node {
		public int value;
		public Node left;
		public Node right;
		public Node parent;

		public Node(int data) {
			this.value = data;
		}
	}

分析：
因为中序遍历是按照 左 -> 头 -> 右的方式进行打印，所以要考虑X所处的位置。

1. 如果X有右树，则X的后继节点一定是右树中的最左节点。
2. 如果X没有右树，则看X是否是X.parent的left节点，如果是，则parent就是X的后继节点，如果不是，则一直向上找。直到找到当前节点是parent的左子节点为止，如果找不到，则说明X是右树最末端节点，后继节点为null。

代码实现：

 public static Node getSuccessorNode(Node node){
        if (node == null){
            return node;
        }
        if (node.right != null){
            return getLeftMost(node.right);
        }else{
            Node parent = node.parent;
            if (parent != null && node != parent.left){
                node = parent;
                parent = node.parent;
            }
            return parent;
        }
    }

    public static Node getLeftMost(Node node){
        if (node == null){
            return node;
        }
        while (node.left != null){
            node = node.left;
        }
        return node;
    }