目录
- Application for Texture(纹理的应用)
- Environment Map(环境光贴图)
- Spherical Environment Map(球形环境光贴图)
- Cube Map(立方体贴图)
- Texture can affect shading!(纹理可以作用于着色)
- How to perturb the normal (in flatland)(如何计算法线如何变化呢?)
- Displacement mapping(位移贴图)
- Provide Precomputed Shading(提供预先计算好的阴影)
- 3D Textures and Volume Rendering(三维纹理和体渲染)
- Introduction to geometry(几何介绍)
- Examples of Geometry(几何的例子)
- Many Ways to Represent Geometry(许多方式来表示几何)
- 隐式的几何
- 显示的几何
- "Implicit" Representations of Geometry(几何的隐式表示)
- "Explicit" Representations of Geometry(几何的显式表示)
- Many Implicit Representations in Graphics
- 代数曲面
- Constructive Solid Geometry(CSG)
- Distance Functions(距离函数)
- Level Set Methods(水平集)
- Fractals(分形)
- 参考资源
Application for Texture(纹理的应用)
继续上节课的内容,纹理的应用部分。
在现代GPU中,我们可以理解纹理就是内存加范围查询,可以做不同范围的查询。
Environment Map(环境光贴图)
我们可以用纹理去描述整个环境光的样子,用环境光去渲染其它物体。

Spherical Environment Map(球形环境光贴图)
我们可以把整个环境光记录在球上,然后把它展开:

但是会出现上下方扭曲的情况:这不是一个均匀的描述

Cube Map(立方体贴图)
为了解决上图中出现的扭曲的情况,使用立方体来记录环境光,然后将其展开:
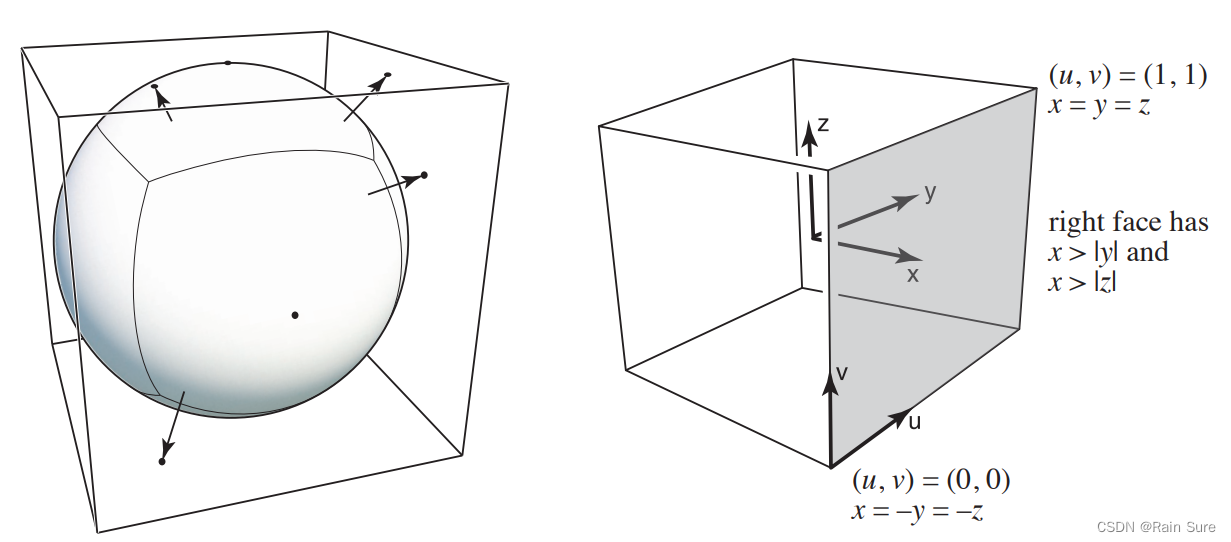
因为立方体六个面都是均匀的,因此很少出现扭曲的情况。
二者的本质是相同的,都是为了描述来自不同方向的光照信息。
Texture can affect shading!(纹理可以作用于着色)
纹理并不只可以用来描述颜色:
我们可以在纹理贴图上定义一个相对高度,这就是凹凸贴图。
如果纹理贴图存储的是法向量,这就是法线贴图。

我们并不需要改变任何几何信息,三角形数量不会改变:
- 对于每个像素,对平面的法向量进行扰动
- 凹凸贴图通过改变高度来改变法线。
How to perturb the normal (in flatland)(如何计算法线如何变化呢?)
首先,考虑简单的情况,在一维版本中:
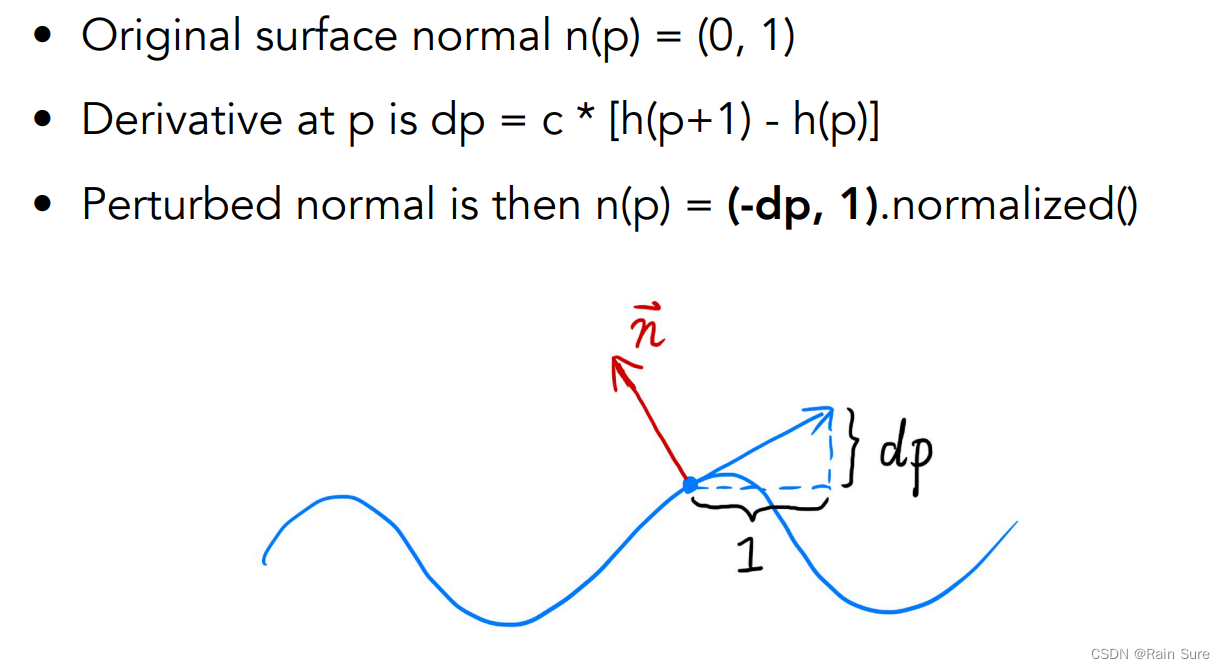
- 假设原始平面的法向量是 n ( p ) = ( 0 , 1 ) n(p) = (0, 1) n(p)=(0,1)
- 那么在凹凸贴图中,点 p p p的切线方向为: c × [ h ( p + 1 ) − h ( p ) ] c \times [h(p + 1) - h(p)] c×[h(p+1)−h(p)],其中常数 c c c是我们自定义的关于凹凸贴图影响的常数。
- 通过切线就可以计算出法线,逆时针旋转90度即可,: n ( p ) = ( − d p , 1 ) n(p) = (-dp, 1) n(p)=(−dp,1),进行归一化即可。
现在,考虑复杂的情况,在三维版本中:
- 假设 p p p点的原始法线为 n ( p ) = ( 0 , 0 , 1 ) n(p) = (0, 0, 1) n(p)=(0,0,1)
-
p
p
p点的切线:分别计算高度关于
u
u
u和
v
v
v的导数
- d p / d u = c 1 ∗ [ h ( u + 1 ) − h ( u ) ] dp / du = c1 * [h(u + 1) - h(u)] dp/du=c1∗[h(u+1)−h(u)]
- d p / d v = c 2 ∗ [ h ( v + 1 ) − h ( v ) ] dp / dv = c2 * [h(v + 1) - h(v)] dp/dv=c2∗[h(v+1)−h(v)]
- 可以得出现在 p p p点的法线为: n ( p ) = ( − d p / d u , − d p / d v , 1 ) n(p) = (-dp / du, -dp / dv, 1) n(p)=(−dp/du,−dp/dv,1),记得做归一化处理。
- 这是局部坐标系中,我们还需要变换回世界坐标系,在作业3中有体现。
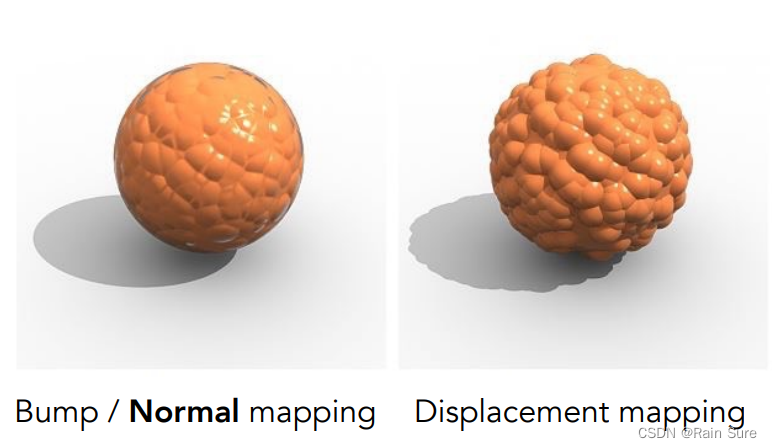
Displacement mapping(位移贴图)
使用纹理来定义任何一点应该有的相对的高度。
和凹凸贴图不同的是,位移贴图真的会让顶点进行移动,顶点位置发生了变化。
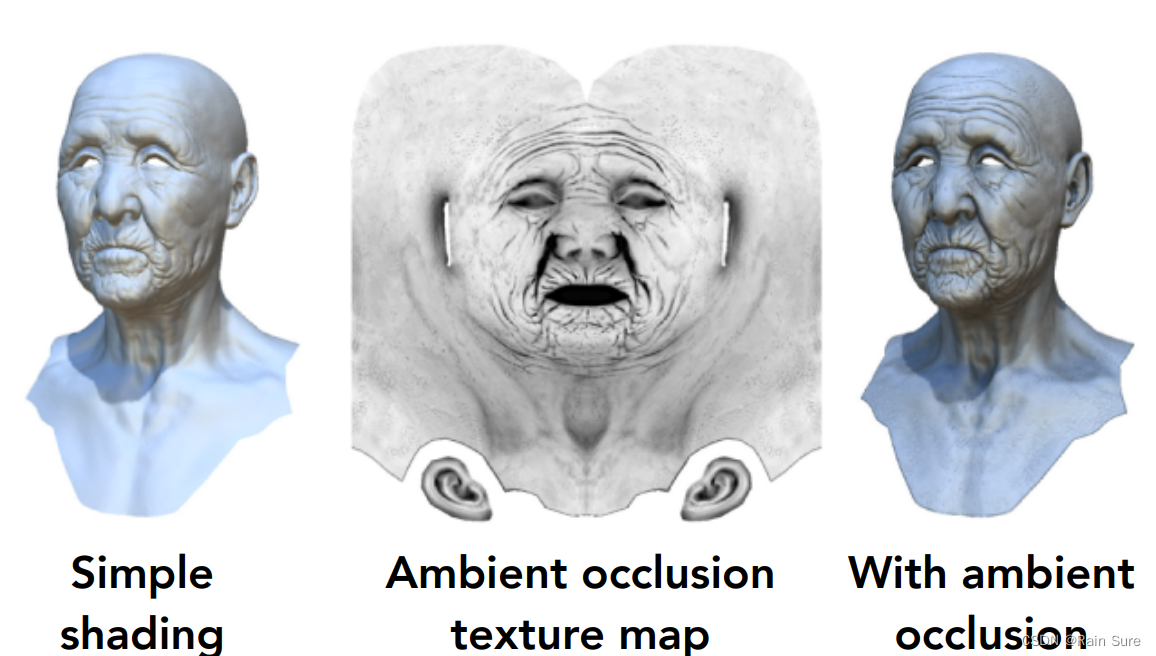
Provide Precomputed Shading(提供预先计算好的阴影)
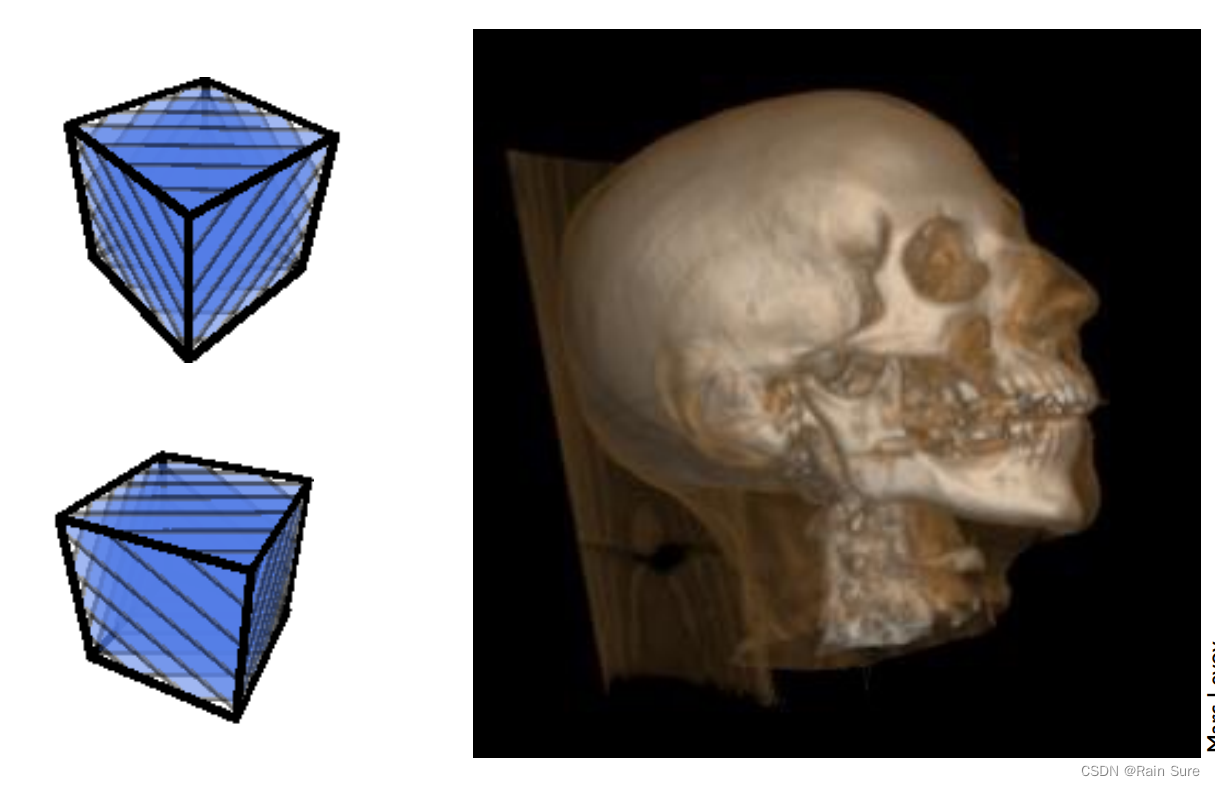
3D Textures and Volume Rendering(三维纹理和体渲染)
具体内容,后续会细致的讲解。
Introduction to geometry(几何介绍)
Examples of Geometry(几何的例子)




Many Ways to Represent Geometry(许多方式来表示几何)
隐式的几何
- 代数曲面
- 水平集,等值集
- 符号距离函数
显示的几何
- 点云
- 多边形网格
- subdivision, NURBS
“Implicit” Representations of Geometry(几何的隐式表示)
定义了空间中的点需要满足的关系:
例如,使用隐式的方法来定义一个球面:
x 2 + y 2 + z 2 = 1 x^2 + y^2 + z^2 = 1 x2+y2+z2=1
更普遍的表示方式: f ( x , y , z ) = 0 f(x, y, z) = 0 f(x,y,z)=0
存在的问题:
哪些点在曲线上呢?
有时会很难看出来:
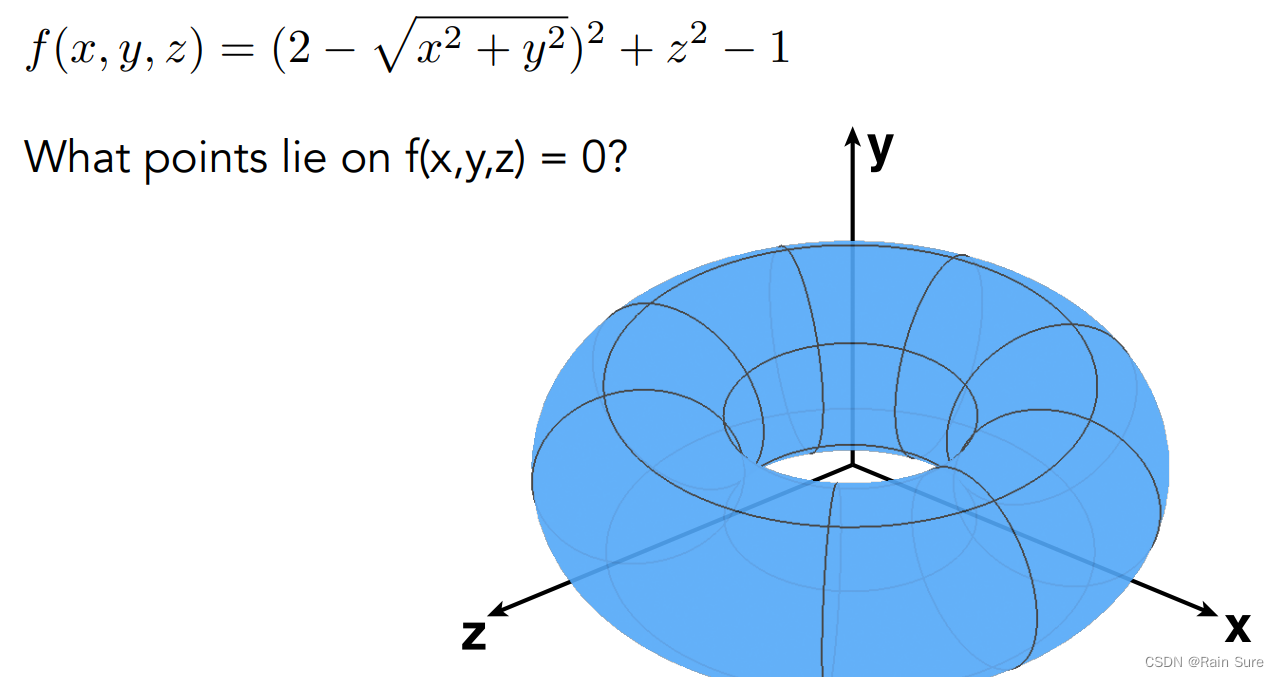
优点:
很容易判断一个点是否在曲面上,或者在里面还是在外面?
只需要把坐标代入表达式,如果是正的就认为在物体外,负的就在物体内部。
“Explicit” Representations of Geometry(几何的显式表示)
所有的点都直接给出活通过参数映射的方式给出:
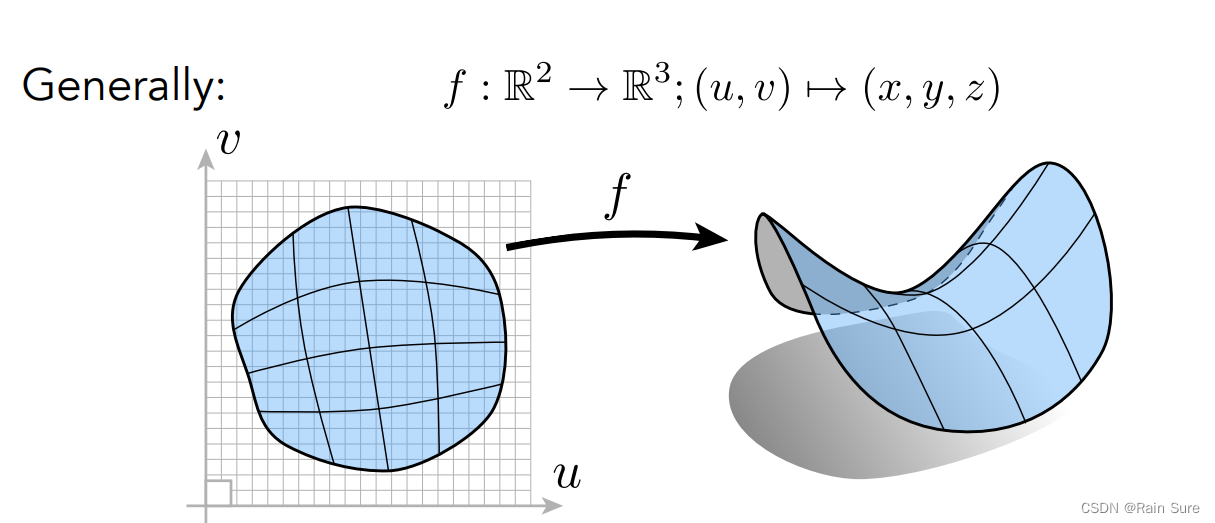
但是,显示的表面很难判断一个点是否在表面上,还是在表面里面或者外面。
根据需要来选择什么样的表示方法
Many Implicit Representations in Graphics
代数曲面
利用数学公式进行表示,缺点就是不直观,上面已经展示过了。

Constructive Solid Geometry(CSG)
通过一系列基本几何的基本布尔运算来定义新的几何:
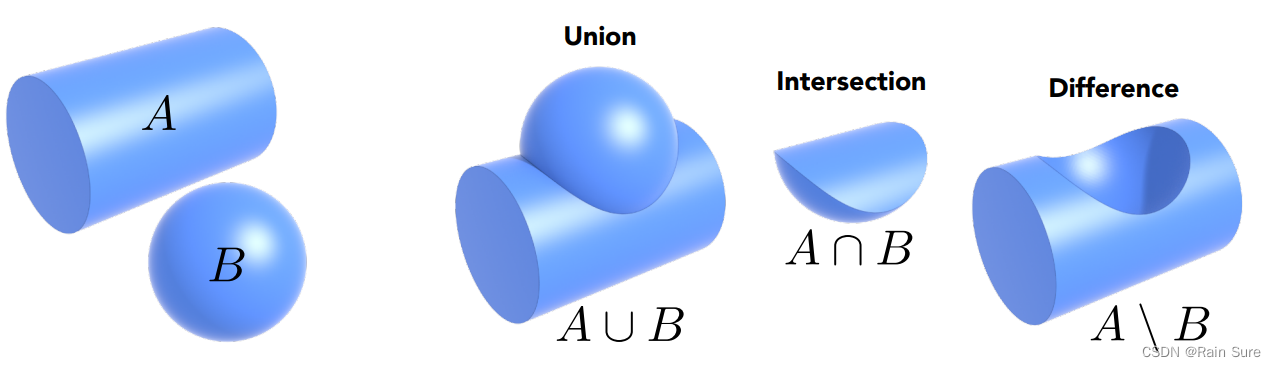
Distance Functions(距离函数)
通过描述一个空间中的任意一个点到曲面的最小距离来定义曲面,这个距离可以是正的可以是负的。
通过使用距离函数来将曲面融合在一起:


Level Set Methods(水平集)
有时候 s d f sdf sdf并不太好通过一些表达式来表示出来,这时候就可以通过水平集的方式进行表示:
我们关注什么地方等于0:
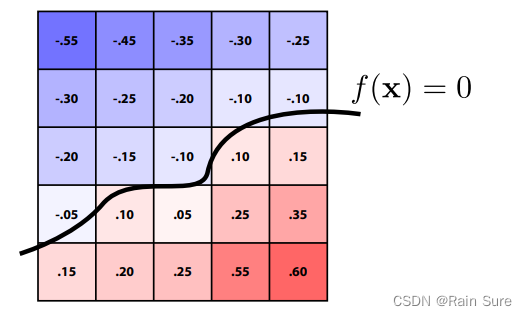
Fractals(分形)
类似递归的思想。

参考资源
GAMES101 Lecture10