Neighborhood Contrastive Learning for Novel Class Discovery (CVPR 2021)
摘要
在本文中,我们解决了新类发现(NCD)的问题,即给定一个具有已知类的有标签数据集,在一组未标记的样本中揭示新的类。我们利用ncd的特性构建了一个新的框架,称为邻域对比学习(NCL),学习对聚类性能至关重要的判别表示。我们的贡献是双重的。首先,我们发现在标记集上训练的特征提取器会生成表示,其中一个通用查询样本和它的邻居可能共享同一个类。我们利用这一观察结果,通过对比学习来检索和聚集伪正对,从而鼓励模型学习更多有区别的表示。其次,我们注意到大多数实例都很容易被网络识别,对对比损失的贡献较小。为了克服这一问题,我们提出了通过在特征空间中混合带标签和无标签样本来产生困难反例的方法。
Baseline for NCD
在baseline中,我们采用和之前工作相似的三阶段学习流程。第一,通过自监督学习,我们同时在有标签数据集和无标签数据集上学习一个没有标签参与的图像表征模型,这种方式已经被证明可以很好的在网络模型的前几层提取低级特征。
接着,无有标签数据集学习高级特征。给定一个样本和对应的标签
(
x
,
y
)
∈
D
l
(x,y) \in D^l
(x,y)∈Dl,我们用交叉熵优化该模型:
ℓ
c
e
=
−
1
C
l
∑
i
=
1
C
l
y
i
log
ϕ
i
l
(
Ω
(
x
)
)
\ell_{c e}=-\frac{1}{C^{l}} \sum_{i=1}^{C^{l}} y_{i} \log \phi_{i}^{l}(\Omega(x))
ℓce=−Cl1i=1∑Clyilogϕil(Ω(x))
最后,我们简化聚类发现的步骤,不再采用统计排名的方式估计两两伪标签,而是采用特征之间的余弦相似度。我们发现,这种修正方式在我们的方法里可以产生相似结果,但是更加高效以及容易实现。具体来说,给定一对从
D
u
D^u
Du中采样的图像
(
x
i
u
,
x
j
u
)
(x^u_i,x^u_j)
(xiu,xju),我们提取特征
(
z
i
u
,
z
j
u
)
(z^u_i,z^u_j)
(ziu,zju)并计算余弦相似度
δ
(
z
i
u
,
z
j
u
)
=
z
i
u
⊤
z
j
u
/
∥
z
i
u
∥
∥
z
j
u
∥
\delta\left(z_{i}^{u}, z_{j}^{u}\right)=z_{i}^{u \top} z_{j}^{u} /\left\|z_{i}^{u}\right\|\left\|z_{j}^{u}\right\|
δ(ziu,zju)=ziu⊤zju/∥ziu∥
zju
,两两伪标签可以通过以下方式分配:
y
^
i
,
j
=
1
[
δ
(
z
i
u
,
z
j
u
)
≥
λ
]
\hat{y}_{i, j}=\mathbb{1}\left[\delta\left(z_{i}^{u}, z_{j}^{u}\right) \geq \lambda\right]
y^i,j=1[δ(ziu,zju)≥λ]
其中
λ
\lambda
λ是表示两个样本分配到同一潜在类别的最小相似度阈值。接着,两两伪标签与无标签头的输出结果之间的内积比较
p
i
,
j
=
ϕ
u
(
z
i
u
)
T
ϕ
u
(
z
j
u
)
p_{i,j}=\phi_u(z^u_i)^T\phi_u(z^u_j)
pi,j=ϕu(ziu)Tϕu(zju)。该模型可以用二元交叉熵优化:
ℓ
b
c
e
=
−
y
^
i
,
j
log
(
p
i
,
j
)
−
(
1
−
y
^
i
,
j
)
log
(
1
−
p
i
,
j
)
\ell_{b c e}=-\hat{y}_{i, j} \log \left(p_{i, j}\right)-\left(1-\hat{y}_{i, j}\right) \log \left(1-p_{i, j}\right)
ℓbce=−y^i,jlog(pi,j)−(1−y^i,j)log(1−pi,j)
我们baselin的最后一个构建块是一致性损失,它迫使网络对图像
x
i
x^i
xi及其相关视图
x
^
i
\hat{x}^i
x^i产生类似的预测。这对于无标签数据尤其重要。尽管如此,我们发现一致性对标注和未标注的样本都有帮助。这一步采用均方误差:
ℓ
m
s
e
=
1
C
l
∑
i
=
1
C
l
(
ϕ
i
l
(
z
l
)
−
ϕ
i
l
(
z
^
l
)
)
2
+
1
C
u
∑
j
=
1
C
u
(
ϕ
j
u
(
z
u
)
−
ϕ
j
u
(
z
^
u
)
)
2
.
\begin{aligned}\ell_{m s e}= & \frac{1}{C^{l}} \sum_{i=1}^{C^{l}}\left(\phi_{i}^{l}\left(z^{l}\right)-\phi_{i}^{l}\left(\hat{z}^{l}\right)\right)^{2}+ \\& \frac{1}{C^{u}} \sum_{j=1}^{C^{u}}\left(\phi_{j}^{u}\left(z^{u}\right)-\phi_{j}^{u}\left(\hat{z}^{u}\right)\right)^{2} .\end{aligned}
ℓmse=Cl1i=1∑Cl(ϕil(zl)−ϕil(z^l))2+Cu1j=1∑Cu(ϕju(zu)−ϕju(z^u))2.
总体损失表示如下:
ℓ
b
a
s
e
=
ℓ
c
e
+
ℓ
b
c
e
+
ω
(
t
)
ℓ
m
s
e
\ell_{b a s e}=\ell_{c e}+\ell_{b c e}+\omega(t) \ell_{m s e}
ℓbase=ℓce+ℓbce+ω(t)ℓmse
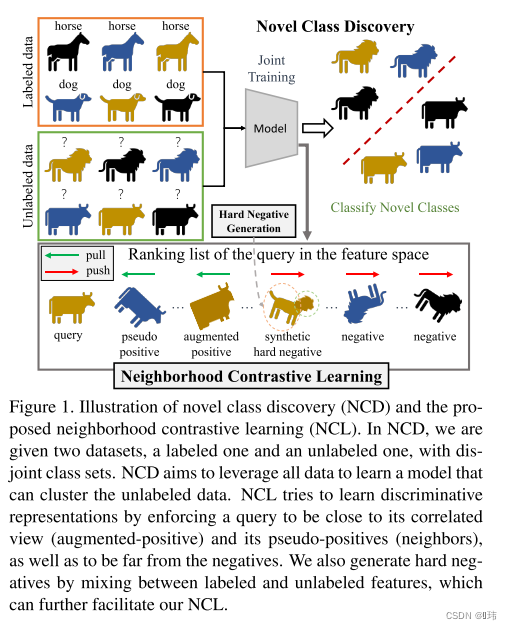
邻里对比学习法(Neighborhood Contrastive Learning, NCL)
给定一系列随机图像变换方式,我们保证一个无标签样本的两个相关视图
(
x
u
,
x
^
u
)
(x^u,\hat{x}^u)
(xu,x^u)被当作正对(positive pair)。接着,我们从视图中用模型提取特征
(
z
u
,
z
^
u
)
(z^u,\hat{z}^u)
(zu,z^u),在大小为
B
B
B的批量数据上执行相同的操作。维持一个查询列表
M
u
M^u
Mu存储过往训练过程中的特征,这些特征最初被认为是不是同一类的,用
z
ˉ
u
\bar{z}^u
zˉu表示。正对的对比损失写作:
ℓ
(
z
u
,
z
^
u
)
=
−
log
e
δ
(
z
u
,
z
^
u
)
/
τ
e
δ
(
z
u
,
z
^
u
)
/
τ
+
∑
m
=
1
∣
M
u
∣
e
δ
(
z
u
,
z
ˉ
m
u
)
/
τ
\ell_{\left(z^{u}, \hat{z}^{u}\right)}=-\log \frac{e^{\delta\left(z^{u}, \hat{z}^{u}\right) / \tau}}{e^{\delta\left(z^{u}, \hat{z}^{u}\right) / \tau}+\sum_{m=1}^{\left|M^{u}\right|} e^{\delta\left(z^{u}, \bar{z}_{m}^{u}\right) / \tau}}
ℓ(zu,z^u)=−logeδ(zu,z^u)/τ+∑m=1∣Mu∣eδ(zu,zˉmu)/τeδ(zu,z^u)/τ
其中
δ
(
⋅
,
⋅
)
\delta(\cdot, \cdot)
δ(⋅,⋅)表示余弦相似度,
τ
\tau
τ是控制分布尺度的温度参数。
不幸的是,对比学习一个出名的缺点就是即使样本属于同一类也会被认为是不同类,由于缺少标签的信息。然而,直观地说,如果正对和负对对应于所期望的潜在类,则表示的质量应该是有益的。一个缓解该问题方式就是模型自身生成伪正对的样本,例如,考虑将表征向量
z
u
z^u
zu的邻居作为同一类的样本。选择合理的伪正对是一项艰巨的任务,特别是在训练开始时,当表征的质量较差。然而,在NCD中,我们可以利用标记的数据集
D
l
D^l
Dl来引导表示,然后使用它们来推断
D
u
D^u
Du中无标签数据之间的关系。
准确来说就是,给定baseline中前两个阶段预寻训练的网络
Ω
\Omega
Ω。我们可以在查询列表中选择和查询向量
z
u
z^u
zu最相近的
t
o
p
−
k
top-k
top−k个相似特征:
ρ
k
=
argtop
z
ˉ
u
(
{
δ
(
z
u
,
z
ˉ
i
u
)
∣
∀
i
∈
{
1
,
…
,
∣
M
u
∣
}
}
)
\rho_{k}=\underset{\bar{z}^{u}}{\operatorname{argtop}}\left(\left\{\delta\left(z^{u}, \bar{z}_{i}^{u}\right) \mid \forall i \in\left\{1, \ldots,\left|M^{u}\right|\right\}\right\}\right)
ρk=zˉuargtop({δ(zu,zˉiu)∣∀i∈{1,…,∣Mu∣}})
假设
ρ
k
\rho_{k}
ρk中的样本都是假负(实际和
z
u
z^u
zu属于同一类),我们可以将它们视为伪正,并将它们在对比损失中的贡献写如下:
ℓ
(
z
u
,
ρ
k
)
=
−
1
k
∑
z
ˉ
i
u
∈
ρ
k
log
e
δ
(
z
u
,
z
ˉ
i
u
)
/
τ
e
δ
(
z
u
,
z
^
u
)
/
τ
+
∑
m
=
1
∣
M
u
∣
e
δ
(
z
u
,
z
ˉ
m
u
)
/
τ
\ell_{\left(z^{u}, \rho_{k}\right)}=-\frac{1}{k} \sum_{\bar{z}_{i}^{u} \in \rho_{k}} \log \frac{e^{\delta\left(z^{u}, \bar{z}_{i}^{u}\right) / \tau}}{e^{\delta\left(z^{u}, \hat{z}^{u}\right) / \tau}+\sum_{m=1}^{\left|M^{u}\right|} e^{\delta\left(z^{u}, \bar{z}_{m}^{u}\right) / \tau}}
ℓ(zu,ρk)=−k1zˉiu∈ρk∑logeδ(zu,z^u)/τ+∑m=1∣Mu∣eδ(zu,zˉmu)/τeδ(zu,zˉiu)/τ
最后,总体损失写作:
ℓ
n
c
l
=
α
ℓ
(
z
u
,
z
^
u
)
+
(
1
−
α
)
ℓ
(
z
u
,
ρ
k
)
\ell_{n c l}=\alpha \ell_{\left(z^{u}, \hat{z}^{u}\right)}+(1-\alpha) \ell_{\left(z^{u}, \rho_{k}\right)}
ℓncl=αℓ(zu,z^u)+(1−α)ℓ(zu,ρk)
其中,
α
\alpha
α控制两个部分的权重。
有监督对比学习
在有标签数据
D
l
D^l
Dl中,我们不需要用网络去挖掘为伪正样本,对于一个样本
x
i
l
x^l_i
xil对应特征
z
i
l
z^l_i
zil,我们可以直接用真实标签检索查询列表
M
l
M^l
Ml取出正例特征:
ρ
=
{
z
ˉ
j
l
∈
M
l
:
y
i
=
y
j
}
∪
z
^
i
l
\rho=\left\{\bar{z}_{j}^{l} \in M^{l}: y_{i}=y_{j}\right\} \cup \hat{z}_{i}^{l}
ρ={zˉjl∈Ml:yi=yj}∪z^il
注意,
ρ
\rho
ρ包含相关视图
x
^
i
L
\hat{x}^L_i
x^iL的
z
^
i
L
\hat{z}^L_i
z^iL和属于同一类的其他样本的特征。利用这种监督方法,可以将邻域对比损失简化为监督对比损失:
ℓ
s
c
l
=
−
1
∣
ρ
∣
∑
z
j
l
∈
ρ
log
e
δ
(
z
i
l
,
z
ˉ
j
l
)
/
τ
e
δ
(
z
i
l
,
z
^
i
l
)
/
τ
+
∑
m
=
1
∣
M
l
∣
e
δ
(
z
i
l
,
z
ˉ
m
l
)
/
τ
\ell_{s c l}=-\frac{1}{|\rho|} \sum_{z_{j}^{l} \in \rho} \log \frac{e^{\delta\left(z_{i}^{l}, \bar{z}_{j}^{l}\right) / \tau}}{e^{\delta\left(z_{i}^{l}, \hat{z}_{i}^{l}\right) / \tau}+\sum_{m=1}^{\left|M^{l}\right|} e^{\delta\left(z_{i}^{l}, \bar{z}_{m}^{l}\right) / \tau}}
ℓscl=−∣ρ∣1zjl∈ρ∑logeδ(zil,z^il)/τ+∑m=1∣Ml∣eδ(zil,zˉml)/τeδ(zil,zˉjl)/τ
Hard Negative Genration
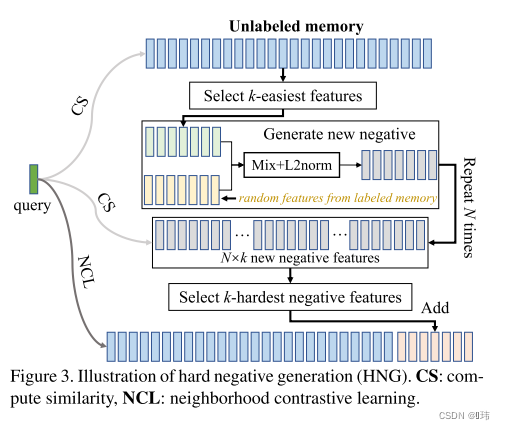
He等人证明了拥有一个极大内存覆盖大量负面样本对对比学习的重要性。最近有研究发现,负面样本和查询样本之间有极低的相似度。我们用实验证明了该现象在出现在我们将对比学习应用在NCD领域中时。我们发现从查询列表中移除最近的消极样本并不会影响性能,这表示这样的消极样本在训练过程中贡献极少。但是并不是我们想要的,这样会浪费内存和计算量。另一方面,自动选择困难的负面样本非常困难,因为我们并没有无标签数据中潜在类别的信息。因此我们可以选择积极样本。然而,在NCD中,我们假设有标签数据和无标签数据中的类别集合是不相交的。这要求一个集合的所有样本对另一个集合的样本是消极的的,反之亦然。受到使用图像/特征混合的正则化技术的进步的启发,我们使用这个概念,通过混合有标签和无标签的样本来生成困难的消极样本。
给定图像的一个视角
x
u
x^u
xu属于无标签数据集,它在特征空间的表征是
z
u
z^u
zu,,我们可以选择简单的负面样本通过查看队列中相似性最小的特征:
ε
k
=
argtop
z
ˉ
i
u
(
{
−
δ
(
z
u
,
z
ˉ
i
u
)
∣
∀
i
∈
{
1
,
…
,
∣
M
u
∣
}
}
)
\varepsilon_{k}=\underset{\bar{z}_{i}^{u}}{\operatorname{argtop}}\left(\left\{-\delta\left(z^{u}, \bar{z}_{i}^{u}\right) \mid \forall i \in\left\{1, \ldots,\left|M^{u}\right|\right\}\right\}\right)
εk=zˉiuargtop({−δ(zu,zˉiu)∣∀i∈{1,…,∣Mu∣}})
注意相似性的负号。由于网络可以自信地从查询中区分这些样本,我们可以安全地假设它们很可能是真正的负面样本,即它们与查询不属于同一类。请注意,这与最近关于挖掘困难的负面样本的文献形成了对比,后者对困难的负面样本进行采样,从而引发了假的负面样本的问题。
让我们也考虑一个查询队列
M
l
M^l
Ml,它包含从过去的训练步骤中存储的有标签样本。如上所述,根据定义,这些是关于
x
u
x^u
xu的真的负面样本。我们的想法是,通过线性插值这两个集合的样本,我们可以产生新的,更有希望有信息的负面样本。在实践中,对于每个
z
ˉ
u
∈
ε
k
\bar{z}^{u} \in \varepsilon_{k}
zˉu∈εk,我们随机抽样一个特征
z
ˉ
u
∈
M
l
\bar{z}^{u} \in M^l
zˉu∈Ml,并计算如下:
ζ
=
μ
⋅
z
ˉ
u
+
(
1
−
μ
)
⋅
z
ˉ
l
\zeta=\mu \cdot \bar{z}^{u}+(1-\mu) \cdot \bar{z}^{l}
ζ=μ⋅zˉu+(1−μ)⋅zˉl
其中,
μ
\mu
μ是混合因子。通过遍历
ε
k
\varepsilon_{k}
εk重复操作
N
N
N次,这样得到的混合消极样本
η
\eta
η包含
k
×
N
k \times N
k×N特征。接着,最苦难的负面样本用余弦相似度从
η
\eta
η中筛选出来:
η
k
=
argtop
ζ
i
(
{
δ
(
z
u
,
ζ
i
)
∣
∀
i
∈
{
1
,
…
,
k
×
N
}
}
)
\eta_{k}=\underset{\zeta_{i}}{\operatorname{argtop}}\left(\left\{\delta\left(z^{u}, \zeta_{i}\right) \mid \forall i \in\{1, \ldots, k \times N\}\right\}\right)
ηk=ζiargtop({δ(zu,ζi)∣∀i∈{1,…,k×N}})
困难的负面样本集合
η
k
\eta_{k}
ηk有以下属性:
- 它们几乎就是真正的反例;
- 对网络来说,很难将它们和查询样本区分开。
最后,我们将新生成的混合反例添加到查询列表 M u M^u Mu:
M u ′ = M u ∪ η k M^{u^{\prime}}=M^{u} \cup \eta_{k} Mu′=Mu∪ηk
然后将上述计算损失值的函数中的 M u M^{u} Mu替换成 M u ′ M^{u^{\prime}} Mu′。
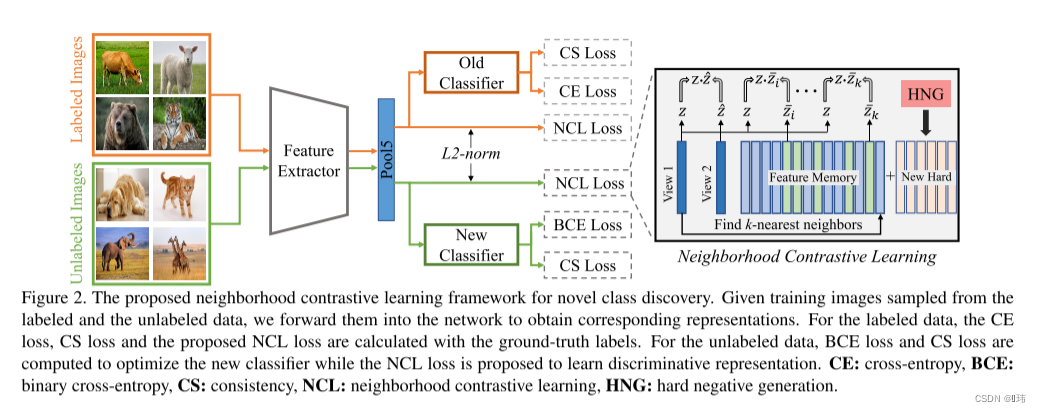
总体损失
考虑基线模型、无标签数据的邻域对比学习、有标签数据的监督对比学习、无标签数据的困难反例生成,我们模型的总体损失为:
ℓ
a
l
l
=
ℓ
b
a
s
e
+
ℓ
n
c
l
+
ℓ
s
c
l
\ell_{a l l}=\ell_{b a s e}+\ell_{n c l}+\ell_{s c l}
ℓall=ℓbase+ℓncl+ℓscl