回归预测 | MATLAB实现PSO-DNN粒子群算法优化深度神经网络的数据多输入单输出回归预测

news2024/10/7 16:27:25

回归预测 | MATLAB实现PSO-DNN粒子群算法优化深度神经网络的数据多输入单输出回归预测

效果一览

基本介绍

回归预测 | MATLAB实现PSO-DNN粒子群算法优化深度神经网络的数据多输入单输出回归预测
MATLAB实现PSO-DNN粒子群算法优化深度神经网络的数据多输入单输出回归预测（Matlab完整程序和数据）
输入7个特征，输出1个，即多输入单输出；
运行环境Matlab2018及以上,运行主程序main即可，其余为函数文件无需运行,所有程序放在一个文件夹,data为数据集；
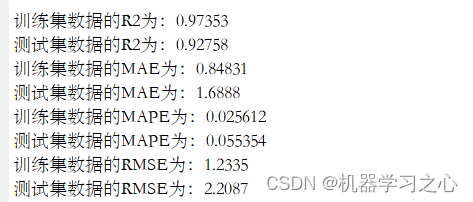
命令窗口输出RMSE、MAE、R2、MAPE。

模型描述

粒子群算法（Particle Swarm Optimization, PSO）是一种启发式优化算法，通常用于解决复杂的非线性优化问题。而分组卷积神经网络（Grouped Convolutional Neural Network, GCNN）是一种卷积神经网络的变体，可以将输入数据分组进行卷积操作，从而减少计算量和参数数量。
针对数据多输入单输出回归预测问题，可以使用粒子群算法来优化分组卷积神经网络的结构和参数，以提高预测准确性。具体步骤如下：

定义目标函数
首先需要定义一个目标函数，用于衡量深度神经网络的预测准确性。一般来说，可以使用均方根误差（RMSE）或者均方误差（MSE）作为目标函数。
确定网络结构和参数
接下来需要确定深度神经网络的结构和参数。可以将这些参数作为粒子的维度，每个粒子代表一个网络结构和参数组合。
初始化粒子群
随机生成一定数量的粒子，每个粒子代表一个网络结构和参数组合。每个粒子都有一个速度和位置，速度表示它的移动方向和速度，位置表示它的当前位置。
更新粒子速度和位置
根据当前粒子的位置和速度，计算下一时刻的速度和位置。更新公式如下：

v_i(t+1) = w * v_i(t) + c1 * rand() * (pbest_i - x_i(t)) + c2 * rand() * (gbest - x_i(t))
x_i(t+1) = x_i(t) + v_i(t+1)
其中，v_i(t)表示粒子i在时刻t的速度，x_i(t)表示粒子i在时刻t的位置，pbest_i表示粒子i历史上最优的位置，gbest表示整个粒子群历史上最优的位置，w、c1和c2是常数，rand()是一个在[0,1]范围内均匀分布的随机数。

计算适应度
根据当前粒子的位置，计算目标函数的值作为粒子的适应度。如果当前位置比历史最优位置更优，则更新历史最优位置。
判断停止条件
如果达到预设的停止条件（如达到最大迭代次数或目标函数值足够小），则停止算法并返回历史最优位置对应的网络结构和参数。
重复步骤4-6
如果没有达到停止条件，则重复步骤4-6，直到达到停止条件为止。
最终得到的历史最优位置对应的网络结构和参数即为经过粒子群算法优化后的分组卷积神经网络，可以用于数据多输入单输出回归预测问题。

程序设计

完整程序和数据下载：后台私信PSO-DNN粒子群算法优化深度神经网络的数据多输入单输出回归预测

%%  参数设置
% ----------------------  修改模型参数时需对应修改fical.m中的模型参数  --------------------------
options = trainingOptions('adam', ...           % Adam 梯度下降算法
         'MaxEpochs', 500, ...                  % 最大训练次数 500
         'InitialLearnRate', best_lr, ...       % 初始学习率 best_lr
         'LearnRateSchedule', 'piecewise', ...  % 学习率下降
         'LearnRateDropFactor', 0.5, ...        % 学习率下降因子 0.1
         'LearnRateDropPeriod', 400, ...        % 经过 400 次训练后 学习率为 best_lr * 0.5
         'Shuffle', 'every-epoch', ...          % 每次训练打乱数据集
         'ValidationPatience', Inf, ...         % 关闭验证
         'L2Regularization', best_l2, ...       % 正则化参数
         'Plots', 'training-progress', ...      % 画出曲线
         'Verbose', false);

%%  训练模型
net = trainNetwork(p_train, t_train, layers, options);

%%  仿真验证
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=double(T_sim1);
T_sim2=double(T_sim2);
%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);
%% 参数初始化
popsize=pop;              %种群规模
lenchrom=dim;              %变量字串长度
fun = fobj;  %适应度函数
pc=0.7;                  %设置交叉概率
pm=0.3;                  %设置变异概率
if(max(size(ub)) == 1)
   ub = ub.*ones(dim,1);
   lb = lb.*ones(dim,1);  
end
maxgen=Max_iter;   % 进化次数  

function [gbest,g,Convergence_curve]=PSO(N,T,lb,ub,dim,fobj)
%% 定义粒子群算法参数
% N 种群 T 迭代次数 
%% 随机初始化种群
D=dim;                   %粒子维数
c1=1.5;                 %学习因子1
c2=1.5;                 %学习因子2
w=0.8;                  %惯性权重

Xmax=ub;                %位置最大值
Xmin=lb;               %位置最小值
Vmax=ub;                %速度最大值
Vmin=lb;               %速度最小值
%%
%%%%%%%%%%%%%%%%初始化种群个体（限定位置和速度）%%%%%%%%%%%%%%%%

x=rand(N,D).*(Xmax-Xmin)+Xmin;
v=rand(N,D).*(Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:N
    pbest(i)=fobj(x(i,:)); 
end
%%%%%%%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%%%%%%%
g=ones(1,D);
gbest=inf;
for i=1:N
    if(pbest(i)<gbest)
        g=p(i,:);
        gbest=pbest(i);
    end
end
%%%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%%%%%%
for i=1:T
    i
    for j=1:N
        %%%%%%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%%%%%
        if (fobj(x(j,:))) <pbest(j)
            p(j,:)=x(j,:);
            pbest(j)=fobj(x(j,:)); 
        end
        %%%%%%%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%%%%
        if(pbest(j)<gbest)
            g=p(j,:);
            gbest=pbest(j);
        end
        %%%%%%%%%%%%%%%%%跟新位置和速度值%%%%%%%%%%%%%%%%%%%%%
        v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
            +c2*rand*(g-x(j,:));
        x(j,:)=x(j,:)+v(j,:);
        %%%%%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%%%%
        if length(Vmax)==1
            for ii=1:D
                if (v(j,ii)>Vmax)  |  (v(j,ii)< Vmin)
                    v(j,ii)=rand * (Vmax-Vmin)+Vmin;
                end
                if (x(j,ii)>Xmax)  |  (x(j,ii)< Xmin)
                    x(j,ii)=rand * (Xmax-Xmin)+Xmin;
                end
            end           
        else
            for ii=1:D
                if (v(j,ii)>Vmax(ii))  |  (v(j,ii)< Vmin(ii))
                    v(j,ii)=rand * (Vmax(ii)-Vmin(ii))+Vmin(ii);
                end
                if (x(j,ii)>Xmax(ii))  |  (x(j,ii)< Xmin(ii))
                    x(j,ii)=rand * (Xmax(ii)-Xmin(ii))+Xmin(ii);
                end
            end
        end
            
    end
    %%%%%%%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%%%%%%%%
   Convergence_curve(i)=gbest;%记录训练集的适应度值

end