Letbook Cookbook题单——数组4

59. 螺旋矩阵 II

难度中等

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FnOybsod-1670475221171)(https://assets.leetcode.com/uploads/2020/11/13/spiraln.jpg)]

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 20

构造一个螺旋矩阵，迭代模拟和递归模拟都可以

迭代

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<int>nums(n*n);
        for(int i=0;i<n*n;i++)
        nums[i]=i+1;
        vector<vector<int>>ans(n,vector<int>(n,0));
        int t=0,len=0,top=0,bottom=n-1,left=0,right=n-1,x,y;
        x=y=0;
        while(len!=n*n)
        {
            ans[y][x]=nums[len++];
            if(x==right&&y==top&&t%4==0)t++,top++;
            else if(x==right&&y==bottom&&t%4==1)t++,right--;
            else if(x==left&&y==bottom&&t%4==2)t++,bottom--;
            else if(x==left&&y==top&&t%4==3)t++,
            left++;
            switch(t%4)
            {
                case 0: x++;break;
                case 1:y++;break;
                case 2:x--;break;
                case 3:y--;break;
            } 
        }
        return ans;
    }
};

递归

class Solution {
public:
vector<vector<int>>ans;
bool vis[21][21]={false};
int dir[4][2]={0,1,1,0,0,-1,-1,0};
int n;
vector<vector<int>>mp;
bool check(int x,int y,int& n)
{
    return x>=0&&y>=0&&x<n&&y<n;
}
void dfs(int x,int y,int d,int n,int pos)
{
    vis[x][y]=true;
    mp[x][y]=pos;
    if(check(x+dir[d][0],y+dir[d][1],n)&&!vis[x+dir[d][0]][y+dir[d][1]])
    dfs(x+dir[d][0],y+dir[d][1],d,n,pos+1);
    else
    {
    d=(d+1)%4;
     if(check(x+dir[d][0],y+dir[d][1],n)&&!vis[x+dir[d][0]][y+dir[d][1]])
     dfs(x+dir[d][0],y+dir[d][1],d,n,pos+1);
     else
     return;
    }
}
    vector<vector<int>> generateMatrix(int n) {
      mp=vector<vector<int>>(n,vector<int>(n));
        dfs(0,0,0,n,1);
        return mp;
    }
};

62. 不同路径

难度中等

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

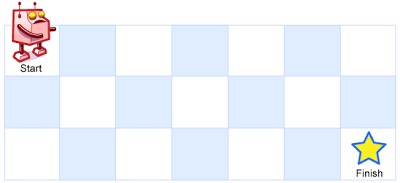
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109

经典dp写法

我们令 dp[i] [j] 是到达 i, j 最多路径

动态方程：dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]

注意，对于第一行 dp[0] [j]，或者第一列 dp[i] [0]，由于都是在边界，所以只能为 1

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
            f[0][j] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
};

数学排列组合

机器人一定会走m+n-2步，即从m+n-2中挑出m-1步向下走，即C（（m+n-2），（m-1））

注意排列组合的求法

class Solution {
public:
    int uniquePaths(int m, int n) {
        long long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
            ans = ans * x / y;
        }
        return ans;
    }
};
/*。

ans = ans * x / y; 疑惑这样一定能保证每次都是整除吗？ 然后手算了一下还真是，例如：

第一次（53 / 1）任何数都可整除1

第二次（53*52 / 1*2）连续的2个数中一定有一个是2的倍数

第三次（53*52*51 / 1*2*3）连续的3个数中一定有一个是3的倍数

以此类推，每次都可以整除
*/

63. 不同路径 II

难度中等924收藏分享切换为英文接收动态反馈

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

和上面本质上是一样的，只要我们强行把障碍物处的路径数置为0就行了，此处使用滚动数组写，节省了一点点空间

滚动数组+dp

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid[0][0])
        return 0;
        int dp[110],m=obstacleGrid.size(),n=obstacleGrid[0].size();
        dp[0]=1;
        for(int i=1;i<n;i++)
        dp[i]=dp[i-1]&&!obstacleGrid[0][i];
        for(int i=1;i<m;i++)
        for(int j=0;j<n;j++)
        {
            if(obstacleGrid[i][j])
            dp[j]=0;
            else if(j>0)
            dp[j]+=dp[j-1];
        }
        return dp[n-1];
    }
};

64. 最小路径和

难度中等1401收藏分享切换为英文接收动态反馈

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例 1：

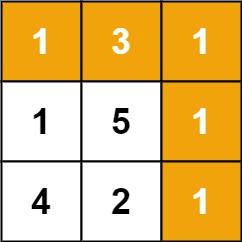
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

滚动数组+dp

和前面差不多

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
       int dp[201]={grid[0][0]};
       for(int i=1;i<grid[0].size();i++)
       dp[i]=dp[i-1]+grid[0][i];
       for(int i=1;i<grid.size();i++)
       for(int j=0;j<grid[0].size();j++)
       {
           if(j==0)
           dp[j]+=grid[i][j];
           else 
           dp[j]=min(grid[i][j]+dp[j],grid[i][j]+dp[j-1]);
       }
       return dp[grid[0].size()-1];
    }
};

66. 加一

难度简单

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。

示例 3：

输入：digits = [0]
输出：[1]

提示：

1 <= digits.length <= 100
0 <= digits[i] <= 9

模拟进位

class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
int n = digits.size();
        for (int i = n - 1; i >= 0; --i) {
            if (digits[i] != 9) {
                ++digits[i];
                for (int j = i + 1; j < n; ++j) {
                    digits[j] = 0;
                }
                return digits;
            }
        }

        // digits 中所有的元素均为 9
        vector<int> ans(n + 1);
        ans[0] = 1;
        return ans;
    }
};

74. 搜索二维矩阵

难度中等

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

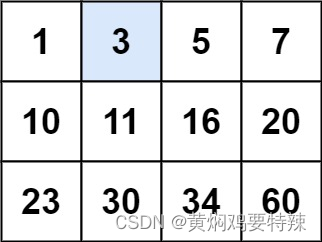
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

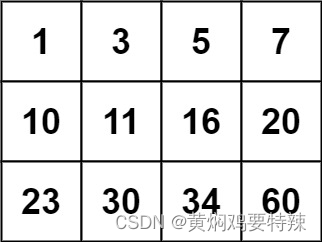
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

两种解法，第一种先对每列进行一次二分查找再对行进行二分查找，第二种直接将二维数组当成一个一维数组，然后对整个一维数组进行二分

两次二分

class Solution {
public:
int binarySearchFirstColumn(vector<vector<int>>& matrix, int target) {
    int low = -1, high = matrix.size() - 1;
    while (low < high) {
        int mid = (high - low + 1) / 2 + low;
        if (matrix[mid][0] <= target) {
            low = mid;
        } else {
            high = mid - 1;
        }
    }
    return low;
}
bool binarySearchRow(vector<int> row, int target) {
    int low = 0, high = row.size() - 1;
    while (low <= high) {
        int mid = (high - low) / 2 + low;
        if (row[mid] == target) {
            return true;
        } else if (row[mid] > target) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return false;
}

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int rowIndex = binarySearchFirstColumn(matrix,target);
    if (rowIndex < 0) {
        return false;
    }
    return binarySearchRow(matrix[rowIndex], target);
}
};

一次二分

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int low = 0, high = m * n - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            int x = matrix[mid / n][mid % n];
            if (x < target) {
                low = mid + 1;
            } else if (x > target) {
                high = mid - 1;
            } else {
                return true;
            }
        }
        return false;
    }
};

78. 子集

难度中等

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

最标准的回溯题

class Solution {
public:
    vector<int> t;
    vector<vector<int>> ans;
    void dfs(int cur, vector<int>& nums) {
        if (cur == nums.size()) {
            ans.push_back(t);
            return;
        }
        t.push_back(nums[cur]);
        dfs(cur + 1, nums);
        t.pop_back();
        dfs(cur + 1, nums);
    }

    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(0, nums);
        return ans;
    }
};

79. 单词搜索

难度中等1493收藏分享切换为英文接收动态反馈

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

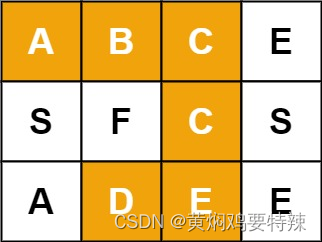
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

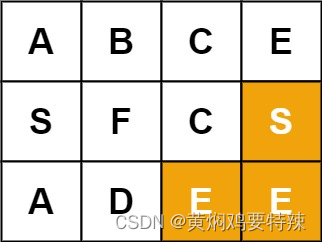
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

上下左右搜索回溯，然后注意选过的不能再选，标记一下

回溯

class Solution {
public:
    // 四个方向的下标偏移量
    int dx[4] = {0, -1, 1, 0};
    int dy[4] = {-1, 0, 0, 1};
    int l, m, n;
    bool res = false;
    void dfs(vector<vector<char>>& board, vector<vector<int>>& visited, string word, int i, int j, int k) {
        // 剪枝，之前的过程中已经找到结果，不用再搜索，直接返回
        if (res) {
            return;
        }
        // 越界或访问过，直接返回
        if (i < 0 || i >= m || j < 0 || j >= n || k >= l || visited[i][j]) {
            return;
        }
        // 字母不匹配，直接返回
        if (board[i][j] != word[k]) {
            return;
        }
        // word判断完毕，存在结果
        if (k == l - 1) {
            res = true;
            return;
        }
        // 递归搜索下一个位置
        visited[i][j] = 1;
        for (int p = 0; p < 4; p++) {
            dfs(board, visited, word, i + dx[p], j + dy[p], k + 1);
        }
        visited[i][j] = 0;
    }
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size();
        n = board[0].size();
        l = word.size();
        vector<vector<int>> visited(m, vector<int>(n));
        // 从网格中的每一个点开始搜索
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 剪枝，之前的过程中没有找到结果，且开始字母一致才需要搜索
                if (!res && board[i][j] == word[0]) {
                    dfs(board, visited, word, i, j, 0);
                }
            }
        }
        return res;
    }
};

80. 删除有序数组中的重复项 II

难度中等

给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

说明：

为什么返回数值是整数，但输出的答案是数组呢？

请注意，输入数组是以**「引用」**方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。 不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,1,2,3,3]
输出：7, nums = [0,0,1,1,2,3,3]
解释：函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。 不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

双指针

数组是有序的，直接上双指针

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if (n <= 2) {
            return n;
        }
        int l = 2, r = 2;
        while (r < n) {
            if (nums[l - 2] != nums[r]) {
                nums[l] = nums[r];
                ++l;
            }
            ++r;
        }
        return l;
    }
};