【paper】 Holographic Embeddings of Knowledge Graphs
【简介】 本文是麻省理工的研究人员发表在 AAAI 2016 上的文章，提出了 HolE(Holographic Embedding)，是一个基于向量循环关联操作的组合向量空间模型。

组合表示

不同论文里对同一类方法的表述不同，这里说的组合表示就是指的双线性这一类模型。模型对于三元组打分函数的定义如下：

其中，∘∘ 代表组合操作，即对头尾实体根据它们的 embedding 创建一个组合向量。

常用的损失函数有两种：

一种是 logistic loss：

另一种是常见的 rank loss：

组合操作 ∘∘ 具体可以有如下几种形式：

Tensor Product

张量积，即 Hardamard 积：

拼接，投影，非线性

⨁⨁ 代表拼接操作，ψψ代表非线性函数 tanhtanh，投影就是指的线性变换。

非组合方法

指的非双线性的 Tran 系列模型：

Holographic Embedding

本文提出的 HolE 定义的组合操作为循环关联（circular correlation）操作：

因此三元组的概率得分为：

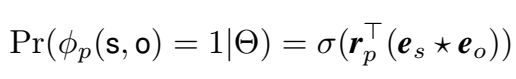
循环关联操作可以被视为张量积的压缩，这样可以在保证较少的计算量的前提下捕捉更多的交互，即保留更多的模型表现力。

HolE 与 RESCAL 的对比：

HolE 的时间复杂度关于维度 d 成拟线性（log线性），并可以通过快速傅里叶变换来计算：

这里用到了复共轭，SEEK 那篇文章提到 HolE 和 ComplEx是等价的。

循环关联操作的直观展示：

与循环卷积的区别：

循环卷积为：

1. 卷积是对称的，满足交换律，而 correlation 不是，

这样可以建模非对称关系。

1. 单个 component 的计算类似点积，

这种特性可以捕捉实体间的相似性。

实验

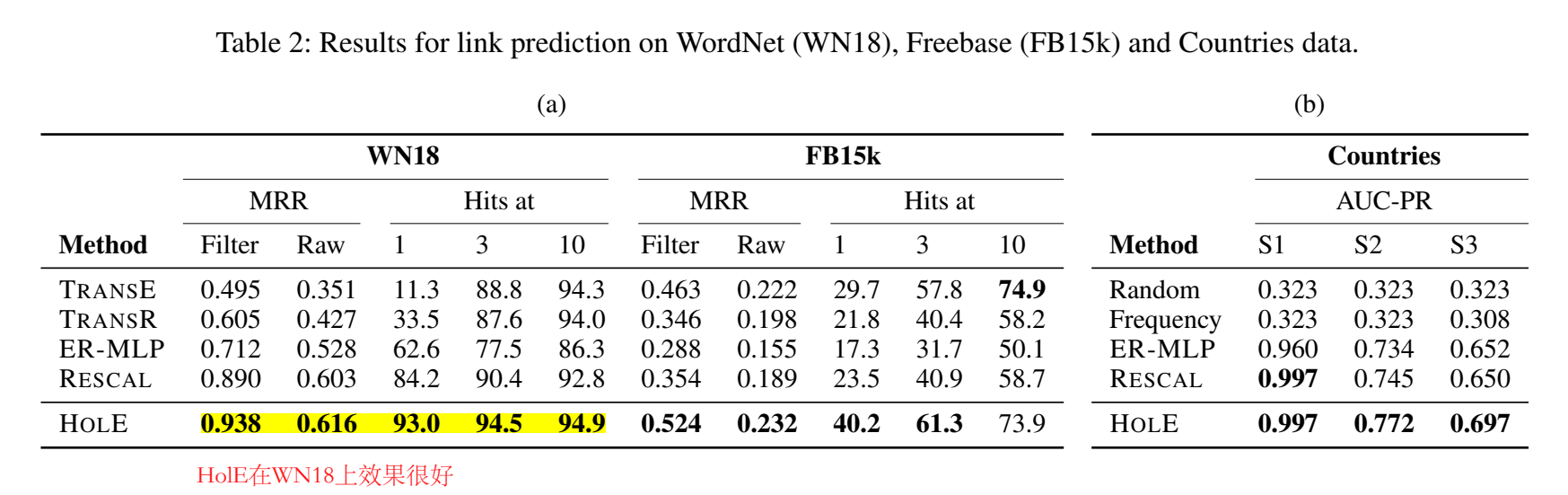
感觉 HolE 的效果比 TransE 提升了很多。

HolE 代码：https://github.com/mnick/holographic-embeddings

---

【小结】 本文提出了使用循环关联操作进行实体向量交互的全息 embedding 方法 HolE，可以在较少的计算量下捕捉到实体间尽可能多的交互。

双线性模型（四）（HolE、ComplEx、NAM） - 胡萝不青菜 - 博客园