matlab可以求解无约束最优化问题、有约束最优化问题和线性规划、二次型规划问题等,同时实现了最小二乘法的曲线拟合方法。matlab求解优化问题的步骤为:
- 写标准型
- 描述目标函数:M-函数或匿名函数
- 用
fminunc()或fmincon()等函数求解原问题。 - 检验得出的解,如随机变换求解的初值,观察是否能得到更好的解。
- 传统最优化方法的最大问题是无法保证得到全局最优解,可以考虑调用matlab的进化算法,如遗传算法和粒子群算法来求解原问题。
1. 无约束最优化问题求解-fminsearch()
无约束最优化问题一般描述为:
min x f ( x ) \min _{\boldsymbol{x}} f(\boldsymbol{x}) xminf(x)
我们的目标是选取合适的 x \boldsymbol{x} x(一个向量)使得目标函数 f ( x ) f(\boldsymbol{x}) f(x)的值最小,最小化是最优化问题的通用描述,如果要求解最大化问题,可以给目标函数 f ( x ) f(\boldsymbol{x}) f(x)添加一个负号转化为求解最小值问题。
matlab提供了基于单纯形法求解无约束的函数的fminsearch(),该函数调用格式为
[ x , f opt , key , c ] = fminsearch (Fun , x 0 , options,附加参数 ) \left.\left[\boldsymbol{x}, f_{\text {opt }},\text {key},\text {c}\right]=\text { fminsearch (Fun }, \boldsymbol{x}_{0}, \text { options,\text{附加参数}}\right) [x,fopt ,key,c]= fminsearch (Fun ,x0, options,附加参数)
其中
- Fun \text{Fun} Fun:要求解问题的数学描述,是一个matlab函数也可以是是一个函数句柄;
- x 0 \boldsymbol{x}_{0} x0:自变量的起始搜索点,需要用户自己定义;
- x \boldsymbol{x} x:寻找到最优值下的自变量的结果。
- f o p t {f}_{\mathrm{opt}} fopt:最优化的目标函数结果。
- key \text{key} key:函数返回的条件,正整数表示已经求解方程的解。而0或负整数表示未搜索到方程的解;
- c \text{c} c:解的附加信息,该变量是一个结构体变量,包含 + iteration: 迭代的次数; + funcCount: 目标函数的调用次数
另外matlab最优化工具箱提供fminunc()和fminsearch()的功能很像,有时候求解无约束最优化问题可以选择该函数。
1.1 例子
我们现在考虑二元函数
min x , y f ( x , y ) = ( x 2 − 2 x ) e − x 2 − y 2 − x y \min _{{x,y}}f(x,y)=(x^2-2x)\mathrm{e}^{-x^2-y^2-xy} x,yminf(x,y)=(x2−2x)e−x2−y2−xy
我们需要做变量代换:令 x 1 = x x_1=x x1=x, x 2 = y x_2=y x2=y, x = [ x 1 , x 2 ] T \boldsymbol{x}=[x_1,x_2]^T x=[x1,x2]T,于是转化目标函数为:
f ( x ) = ( x 1 2 x 1 ) e − x 1 2 − x 2 2 − x 1 x 2 f(\boldsymbol{x})=(x_1^2x_1)\mathrm{e}^{-x_1^2-x_2^2-x_1x_2} f(x)=(x12x1)e−x12−x22−x1x2
f=@(x)(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2));
x0=rand(2,1);[x,f1]=fminsearch(f,x0)
解得:

2. 有约束最优化问题求解-fmincon()
min x f ( x ) s.t. { A x ⩽ B A e q x = B e q x m ⩽ x ⩽ x M C ( x ) ⩽ 0 C e q ( x ) = 0 \min _{\boldsymbol{x}} f(\boldsymbol{x})\\ \text { s.t. }\left\{\begin{array}{l} \boldsymbol{A} \boldsymbol{x} \leqslant \boldsymbol{B} \\ \boldsymbol{A}_{\mathrm{eq}} \boldsymbol{x}=\boldsymbol{B}_{\mathrm{eq}} \\ \boldsymbol{x}_{\mathrm{m}} \leqslant \boldsymbol{x} \leqslant \boldsymbol{x}_{\mathrm{M}} \\ \boldsymbol{C}(\boldsymbol{x}) \leqslant \mathbf{0} \\ \boldsymbol{C}_{\mathrm{eq}}(\boldsymbol{x})=\mathbf{0} \end{array}\right. xminf(x) s.t. ⎩ ⎨ ⎧Ax⩽BAeqx=Beqxm⩽x⩽xMC(x)⩽0Ceq(x)=0
可以看到约束可以是线性等式约束(第1个式子)也可以是线性不等式约束(第2个式子),可以是有界约束(第3个式子),还可以是非线性约束(第4个和第5个式子)。在matlab里提供了一个fmincon()函数,专门用于求解各种约束下的最优化问题,其调用方式为:
[ x , f opt , key,c ] = fmincon ( Fun , x 0 , A , B , A e q , B e q , x m , x M , CFun,OPT ) \left[\boldsymbol{x}, f_{\text {opt}}, \text {key,c}\right]=\text {fmincon}\left(\text {Fun}, \boldsymbol{x}_{0}, \boldsymbol{A}, \boldsymbol{B}, \boldsymbol{A}_{\mathrm{eq}}, \boldsymbol{B}_{\mathrm{eq}}, \boldsymbol{x}_{\mathrm{m}}, \boldsymbol{x}_{\mathrm{M}}, \text {CFun,OPT}\right) [x,fopt,key,c]=fmincon(Fun,x0,A,B,Aeq,Beq,xm,xM,CFun,OPT)
其中
- Fun \text{Fun} Fun:给目标函数写的m-函数;
- x 0 \boldsymbol{x}_{0} x0:自变量的起始搜索点,需要用户自己定义;
- 线性约束如果不存在用空矩阵来占位
- x \boldsymbol{x} x:寻找到最优值下的自变量的结果。
- f o p t {f}_{\mathrm{opt}} fopt:最优化的目标函数结果。
- CFun \text{CFun} CFun:给非线性函数写的m-函数;
- OPT \text{OPT} OPT:控制选项。
如果在最优化过程中发现找不到可行解,在求解结束后将给出提示:No feasible solution found
有约束优化还有几种特殊的方式,如线性规划、二次型规划问题,可以使用工具箱的linprog()和quadprog()函数直接求解。此外,整数规划、0-1规划等问题可以由专门的工具求解,下面给出一般非线性规划问题的最优化求解。
2.1 例子1
min x 0.6224 x 1 x 2 x 3 x 4 + 1.7781 x 2 x 3 2 + 3.1661 x 1 2 x 4 + 19.84 x 1 2 x 3 ) s.t. { 0.0193 x 3 − x 1 ≤ 0 0.00954 x 3 − x 2 ≤ 0 750 × 1728 − π x 3 2 x 4 − 4 π x 3 3 / 3 ≤ 0 x 4 − 240 ≤ 0 0.0625 ≤ x 1 , x 2 ≤ 6.1875 , 10 ≤ x 3 , x 4 ≤ 200 \min _{\boldsymbol{x}} 0.6224x_1x_2x_3x_4+1.7781x_2x_3^2+3.1661x_1^2x_4+19.84x_1^2x_3)\\ \text { s.t. }\left\{\begin{array}{l} 0.0193x_3-x_1\le0\\ 0.00954x_3-x_2\le0\\ 750\times 1728-\pi x_3^2x_4-4\pi x_3^3/3\le0 x_4-240\le0\\ 0.0625\le x_1,x_2\le 6.1875,10\le x_3,x_4\le 200 \end{array}\right. xmin0.6224x1x2x3x4+1.7781x2x32+3.1661x12x4+19.84x12x3) s.t. ⎩ ⎨ ⎧0.0193x3−x1≤00.00954x3−x2≤0750×1728−πx32x4−4πx33/3≤0x4−240≤00.0625≤x1,x2≤6.1875,10≤x3,x4≤200
main
% 定义目标函数
f=@(x)0.6224*x(1)*x(2)*x(3)*x(4)+1.7781*x(2)*x(3)^2+3.1661*x(1)^2*x(4)+19.84*x(1)^2*x(3);
% 定义求解条件
xm=[0.0625,0.0625,10,10];
xM=[6.1875,6.1875,200,200];
A=[];
B=[];
Aeq=[];
Beq=[];
x0=(xm+xM)/2;
ff=optimset;
ff.Tolx=1e-10;
ff.TolFun=1e-20;
[x,f]=fmincon(f,x0,A,B,Aeq,Beq,xm,xM,@constraint,ff)
由于约束函数要返回两个变量:等式约束
c
e
q
\mathrm{ceq}
ceq和不等式约束
c
\mathrm{c}
c。这里便不能用匿名函数来定义,原问题只有不等式约束,没有等式约束,所以返回的是空矩阵
constraint
% 定义非线性约束
function [c,ceq] = constraint(x)
c=[0.0193*x(3)-x(1);
0.00954*x(3)-x(2);
750*1728-pi*x(3)^2*x(4)-4*pi*x(3)^3/3;
x(4)-240];
ceq=[];
end
运行main函数,最后我们得到的是:

有时候我们可能找不到最优解,这时候我们会提示:
Maximum number of function evaluations exceeded:
increase options.MaxFunEvals
这时候我们可能需要改进搜索的初值,或者修改控制参数OPT,再进行寻优,得到期望的最优值。
2.2 例子2
min q , w , k k s.t. { q 3 + 9.625 q 1 w + 16 q 2 w + 16 w 2 + 12 − 4 q 1 − q 2 − 78 w = 0 16 q 1 w + 44 − 19 q 1 − 8 q 2 − q 3 − 24 w = 0 2.25 − 0.25 k ≤ q 1 ≤ 2.25 + 0.25 k 1.5 − 0.5 k ≤ q 2 ≤ 1.5 + 0.5 k 1.5 − 1.5 k ≤ q 3 ≤ 1.5 + 1.5 k \min _{\boldsymbol{q},w,k} k\\ \text { s.t. }\left\{\begin{array}{l} q_3+9.625q_1w+16q_2w+16w^2+12-4q_1-q_2-78w=0\\ 16q_1w+44-19q_1-8q_2-q_3-24w=0\\ 2.25-0.25k\le q_1\le 2.25+0.25k\\ 1.5-0.5k\le q_2\le 1.5+0.5k\\ 1.5-1.5k\le q_3\le 1.5+1.5k \end{array}\right. q,w,kmink s.t. ⎩ ⎨ ⎧q3+9.625q1w+16q2w+16w2+12−4q1−q2−78w=016q1w+44−19q1−8q2−q3−24w=02.25−0.25k≤q1≤2.25+0.25k1.5−0.5k≤q2≤1.5+0.5k1.5−1.5k≤q3≤1.5+1.5k
我们首先需要对变量做替换:
x 1 = q 1 , x 2 = q 2 , x 3 = q 3 , x 4 = w , x 5 = k x_1=q_1,x_2=q_2,x_3=q_3,x_4=w,x_5=k x1=q1,x2=q2,x3=q3,x4=w,x5=k
并且需要对不等式重新进行整理:
min x x 5 s.t. { x 3 + 9.625 x 1 x 4 + 16 x 2 x 4 + 16 x 4 2 + 12 − 4 x 1 − x 2 − 78 x 4 = 0 16 x 1 x 4 + 44 − 19 x 1 − 8 x 2 − x 3 − 24 x 4 = 0 − 0.25 x 5 − x 1 ≤ − 2.25 x 1 − 0.25 x 5 ≤ 2.25 − 0.5 x 5 − x 2 ≤ − 1.5 x 2 − 0.5 x 5 ≤ 1.5 − 1.5 x 5 − x 3 ≤ − 1.5 x 3 − 1.5 x 5 ≤ 1.5 \min _{\boldsymbol{x}} x_5\\ \text { s.t. }\left\{\begin{array}{l} x_3+9.625x_1x_4+16x_2x_4+16x_4^2+12-4x_1-x_2-78x_4=0\\ 16x_1x_4+44-19x_1-8x_2-x_3-24x_4=0\\ -0.25x_5-x_1\le-2.25\\ x_1-0.25x_5\le 2.25\\ -0.5x_5-x_2\le-1.5\\ x_2-0.5x_5\le 1.5\\ -1.5x_5-x_3\le-1.5\\ x_3-1.5x_5\le 1.5\\ \end{array}\right. xminx5 s.t. ⎩ ⎨ ⎧x3+9.625x1x4+16x2x4+16x42+12−4x1−x2−78x4=016x1x4+44−19x1−8x2−x3−24x4=0−0.25x5−x1≤−2.25x1−0.25x5≤2.25−0.5x5−x2≤−1.5x2−0.5x5≤1.5−1.5x5−x3≤−1.5x3−1.5x5≤1.5
原问题有两个非线性等式约束,没有不等式约束。非线性约束条件描述
constraint
function [c,ceq] = constraint(x)
c=[];
ceq=[x(3)+9.625*x(1)*x(4)+16*x(2)*x(4)+16*x(4)^2+12-4*x(1)-x(2)-78*x(4);
16*x(1)*x(4)+44-19*x(1)-8*x(2)-x(3)-24*x(4)];
end
线性不等式约束我们写作 A x ≤ b \mathbf{Ax}\le \mathbf{b} Ax≤b,其中:
A = [ − 1 0 0 0 − 0.25 1 0 0 0 − 0.25 0 − 1 0 0 − 0.5 0 1 0 0 − 0.5 0 0 − 1 0 − 1.5 0 0 1 0 − 1.5 ] , b = [ − 2.25 2.25 − 1.5 1.5 − 1.5 1.5 ] \mathbf{A}=\begin{bmatrix} -1& 0& 0 & 0 & -0.25\\ 1& 0 & 0 & 0 & -0.25\\ 0 & -1 & 0 & 0 & -0.5\\ 0 & 1 & 0 & 0 & -0.5\\ 0 & 0 & -1 & 0 & -1.5\\ 0 & 0 & 1 &0 &-1.5 \end{bmatrix},\mathbf{b}=\begin{bmatrix} -2.25\\ 2.25 \\ -1.5 \\ 1.5\\ -1.5 \\ 1.5 \end{bmatrix} A= −11000000−11000000−11000000−0.25−0.25−0.5−0.5−1.5−1.5 ,b= −2.252.25−1.51.5−1.51.5
该问题没有线性等式约束,也没有决策变量的下界和上界约束,所以可以将这些约束用空矩阵表示:
main
f=@(x)x(5);
xm=[];
xM=[];
A=[-1,0,0,0,-0.25;1,0,0,0,-0.25;0,-1,0,0,-0.5;0,1,0,0,-0.5;0,0,-1,0,-1.5;0,0,1,0,-1.5];
B=[-2.25;2.25;-1.5;1.5;-1.5;1.5];
Aeq=[];
Beq=[];
x0=2*rand(5,1);
[x,f]=fmincon(f,x0,A,B,Aeq,Beq,xm,xM,@constraint)
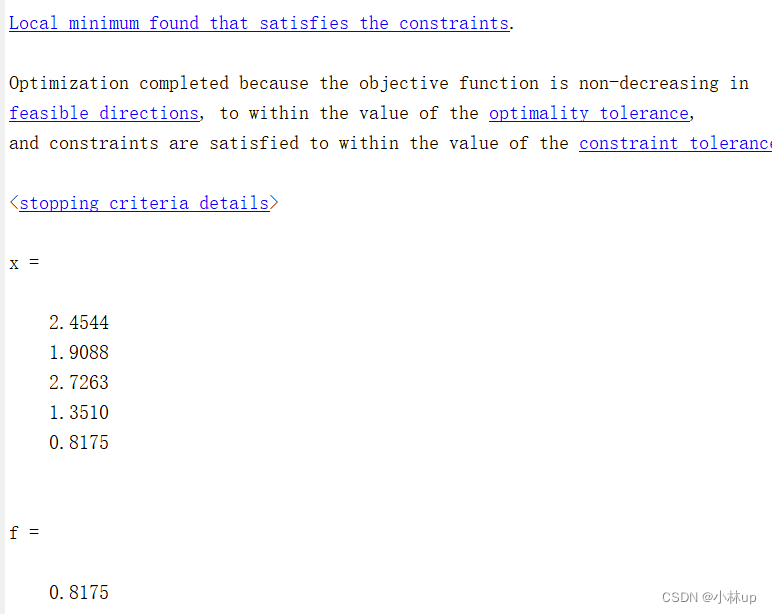
求解的时候很可能求出局部最优解 x 5 = 1.1448 x_5=1.1448 x5=1.1448,多调用几次就会得到全局最优解 x = [ 2.4544 , 1.9088 , 2.7263 , 1.3510 , 0.8175 ] T \boldsymbol{x}=[2.4544,1.9088,2.7263,1.3510,0.8175]^T x=[2.4544,1.9088,2.7263,1.3510,0.8175]T,目标函数为 0.8175 0.8175 0.8175。

参考资料:
[1] 薛定宇.《控制系统仿真与计算机辅助设计》.第3版