1. 图的基本概念

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E) ，其中：

顶点集合 V = {x|x 属于某个数据对象集 } 是有穷非空集合 ； E = {(x,y)|x,y 属于 V} 或者 E = {<x, y>|x,y 属于 V && Path(x, y)} 是顶点间关系的有穷集合，也叫 做边的集合 。 (x, y)表示 x 到 y 的一条双向通路，即 (x, y) 是无方向的； Path(x, y) 表示从 x 到 y 的一条单向通路，即 Path(x, y)是有方向的。顶点和边：图中结点称为顶点 ，第 i 个顶点记作 vi 。 两个顶点 vi 和 vj 相关联称作顶点 vi 和顶点 vj 之间 有一条边 ，图中的第 k 条边记作 ek ， ek = (vi ， vj) 或 <vi ， vj> 。有向图和无向图：在有向图中，顶点对 <x, y> 是有序的，顶点对 <x ， y> 称为顶点 x 到顶点 y 的一条 边 ( 弧 ) ， <x, y> 和 <y, x> 是两条不同的边 ，比如下图 G3 和 G4 为有向图。在 无向图中，顶点对 (x, y) 是无序的，顶点对 (x,y) 称为顶点 x 和顶点 y 相关联的一条边，这条边没有特定方向， (x, y) 和 (y ， x) 是同一条边 ，比如下图 G1 和 G2 为无向图。注意： 无向边 (x, y) 等于有向边 <x, y> 和 <y, x> 。

完全图：在有 n 个顶点的无向图中 ，若有 n * (n-1)/2 条边，即 任意两个顶点之间有且仅有一条边 ，

则称此图为 无向完全图 ，比如上图 G1 ；在 n 个顶点的有向图 中，若有 n * (n-1) 条边，即 任意两个

顶点之间有且仅有方向相反的边 ，则称此图为 有向完全图 ，比如上图 G4 。

邻接顶点：在 无向图中 G 中，若 (u, v) 是 E(G) 中的一条边，则称 u 和 v 互为邻接顶点 ，并称边 (u,v) 依

附于顶点 u 和 v ；在 有向图 G 中，若 <u, v> 是 E(G) 中的一条边，则称顶点 u 邻接到 v ，顶点 v 邻接自顶

点 u ，并称边 <u, v> 与顶点 u 和顶点 v 相关联 。

顶点的度：顶点 v 的度是指与它相关联的边的条数，记作 deg(v) 。在有向图中， 顶点的度等于该顶

点的入度与出度之和 ，其中顶点 v 的 入度是以 v 为终点的有向边的条数 ，记作 indev(v); 顶点 v 的出度

是以 v 为起始点的有向边的条数 ，记作 outdev(v) 。因此： dev(v) = indev(v) + outdev(v) 。注

意：对于 无向图，顶点的度等于该顶点的入度和出度 ，即 dev(v) = indev(v) = outdev(v) 。路径：在图G = (V ， E) 中，若 从顶点 vi 出发有一组边使其可到达顶点 vj ，则称顶点 vi 到顶点 vj 的顶 点序列为从顶点 vi 到顶点 vj 的路径 。路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数 ；对于 带权的图，一 条路 径的路径长度是指该路径上各个边权值的总和 。

简单路径与回路： 若路径上各顶点 v1 ， v2 ， v3 ， … ， vm 均不重复，则称这样的路径为简单路

径。若路 径上第一个顶点 v1 和最后一个顶点 vm 重合，则称这样的路径为回路或环 。

子图：设图 G = {V, E} 和图 G1 = {V1 ， E1} ，若 V1 属于 V 且 E1 属于 E ，则称 G1 是 G 的子图 。

连通图：在 无向图 中，若从顶点 v1 到顶点 v2 有路径，则称顶点 v1 与顶点 v2 是连通的。 如果图中任

意一 对顶点都是连通的，则称此图为连通图 。

强连通图：在 有向图 中，若在 每一对顶点 vi 和 vj 之间都存在一条从 vi 到 vj 的路径，也存在一条从 vj

到 vi 的路径，则称此图是强连通图 。

生成树：一个 连通图的最小连通子图 称作该图的生成树。有 n 个顶点的连通图的生成树有 n 个顶点

和 n- 1 条边。

2. 图的存储结构

因为图中既有节点，又有边 ( 节点与节点之间的关系 ) ，因此， 在图的存储中，只需要保存：节点和

边关系即可 。节点保存比较简单，只需要一段连续空间即可，那边关系该怎么保存呢？

2.1 邻接矩阵

因为节点与节点之间的关系就是连通与否，即为 0 或者 1 ，因此 邻接矩阵 ( 二维数组 ) 即是：先用一

个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系 。

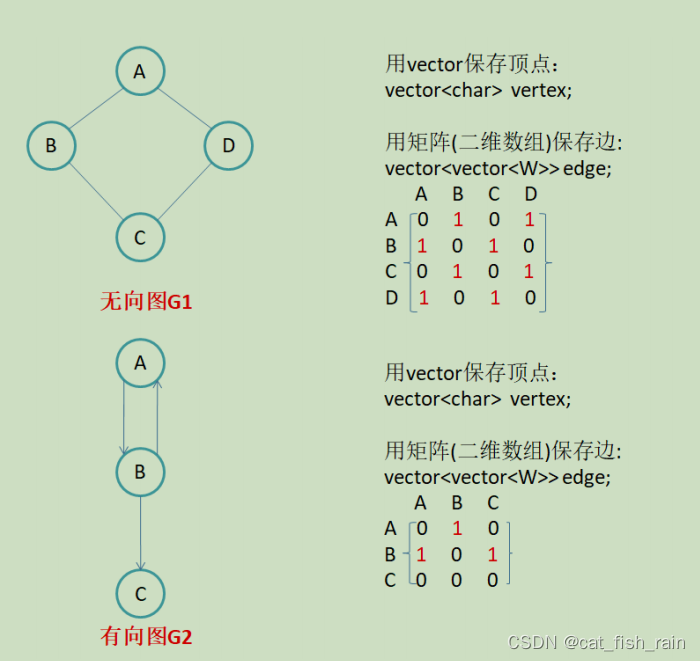
注意：

1. 无向图的邻接矩阵是对称的 ，第 i 行 ( 列 ) 元素之和，就是顶点 i 的度。 有向图的邻接矩阵则不一 定是对称的，第 i 行 ( 列 ) 元素之后就是顶点 i 的出 ( 入 ) 度。

2. 如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个顶点不通，则使用无穷大代替。

3. 用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0 成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求。

#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;

template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
    typedef Graph<V, W, MAX_W, Direction> Self;
    Graph() = default;
    Graph(const V *vertexs, size_t n)
    {
        _vertexs.reserve(n);
        for (size_t i = 0; i < n; ++i)
        {
            _vertexs.push_back(vertexs[i]);
            _vIndexMap[vertexs[i]] = i;
        }
        // MAX_W 作为不存在边的标识值
        _matrix.resize(n);
        for (auto &e : _matrix)
        {
            e.resize(n, MAX_W);
        }
    }
    size_t GetVertexIndex(const V &v)
    {
        auto ret = _vIndexMap.find(v);
        if (ret != _vIndexMap.end())
        {
            return ret->second;
        }
        else
        {
            throw invalid_argument("不存在的顶点");
            return -1;
        }
    }
    void _AddEdge(size_t srci, size_t dsti, const W &w)
    {
        _matrix[srci][dsti] = w;
        if (Direction == false)
        {
            _matrix[dsti][srci] = w;
        }
    }
    void AddEdge(const V &src, const V &dst, const W &w)
    {
        size_t srci = GetVertexIndex(src);
        size_t dsti = GetVertexIndex(dst);
        _AddEdge(srci, dsti, w);
    }

    void Print()
    {
        // 打印顶点和下标映射关系
        for (size_t i = 0; i < _vertexs.size(); ++i)
        {
            cout << _vertexs[i] << "-" << i << " ";
        }
        cout << endl
             << endl;
        cout << " ";
        for (size_t i = 0; i < _vertexs.size(); ++i)
        {
            cout << i << " ";
        }
        cout << endl;
        // 打印矩阵
        for (size_t i = 0; i < _matrix.size(); ++i)
        {
            cout << i << " ";
            for (size_t j = 0; j < _matrix[i].size(); ++j)
            {
                if (_matrix[i][j] != MAX_W)
                    cout << _matrix[i][j] << " ";
                else
                    cout << "#"
                         << " ";
            }
            cout << endl;
        }
        cout << endl
             << endl;
        // 打印所有的边
        for (size_t i = 0; i < _matrix.size(); ++i)
        {
            for (size_t j = 0; j < _matrix[i].size(); ++j)
            {
                if (i < j && _matrix[i][j] != MAX_W)
                {
                    cout << _vertexs[i] << "-" << _vertexs[j] << ":" << _matrix[i][j] << endl;
                }
            }
        }
    }

private:
    map<V, size_t> _vIndexMap;
    vector<V> _vertexs; // 顶点集合
    vector<vector<W>> _matrix;
    // 存储边集合的矩阵
};
void TestGraph()
{
    Graph<char, int, INT_MAX, true> g("0123", 4);
    g.AddEdge('0', '1', 1);
    g.AddEdge('0', '3', 4);
    g.AddEdge('1', '3', 2);
    g.AddEdge('1', '2', 9);
    g.AddEdge('2', '3', 8);
    g.AddEdge('2', '1', 5);
    g.AddEdge('2', '0', 3);
    g.AddEdge('3', '2', 6);
    g.Print();
}

int main()
{
    TestGraph();
    system("pause");
    return 0;
}

2.2 邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系。

1. 无向图邻接表存储

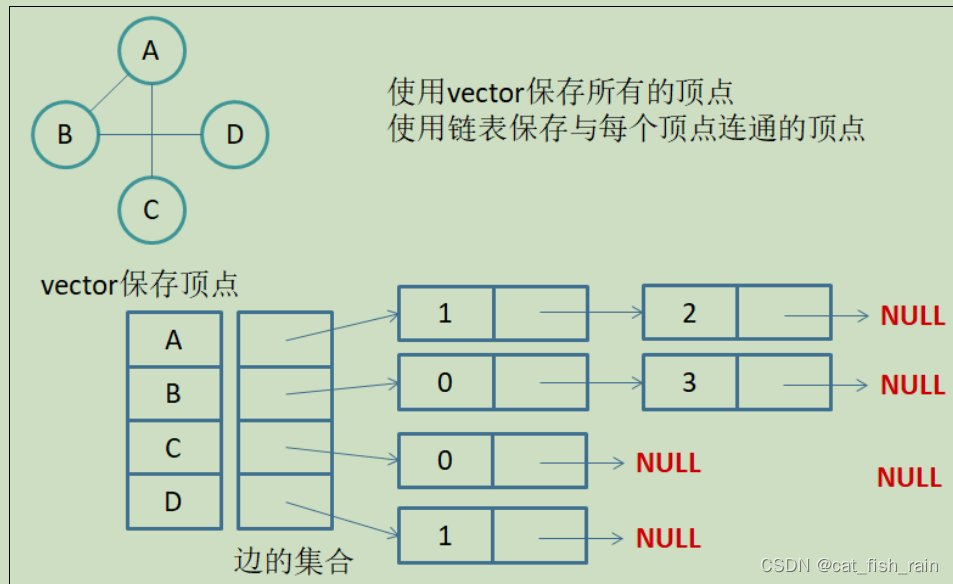
注意： 无向图中同一条边在邻接表中出现了两次。如果想知道顶点 vi 的度，只需要知道顶点 vi 边链表集合中结点的数目即可 。

2. 有向图邻接表存储

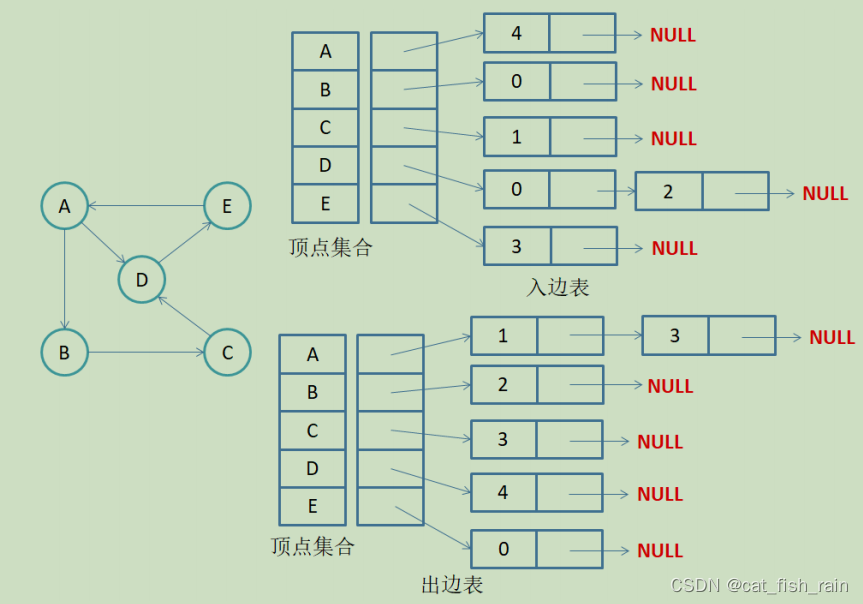
注意：有向图中每条边在邻接表中只出现一次，与顶点 vi 对应的邻接表所含结点的个数，就是该顶点的出度，也称出度表，要得到vi 顶点的入度，必须检测其他所有顶点对应的边链表，看有多少边顶点的dst 取值是 i 。

#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;

namespace LinkTable
{

    template <class W>
    struct LinkEgde
    {
        int _srcIndex;
        int _dstIndex;
        W _w;
        LinkEgde<W> *_next;

        LinkEgde(const W &w) : _srcIndex(-1), _dstIndex(-1), _w(w), _next(nullptr) {}
    };

    template <class V, class W, bool Direction = false>
    class Graph
    {

        typedef LinkEgde<W> Edge;

    public:
        Graph(const V *vertexs, size_t n)
        {

            _vertexs.reserve(n);
            for (size_t i = 0; i < n; i++)
            {

                _vertexs.push_back(_vertexs[i]);
                _vIndexMap[_vertexs[i]] = i;
            }
            _linkTable.resize(n, nullptr);
        }
        size_t GetVertexIndex(const V &v)
        {

            auto ret = _vIndexMap.find(v);
            if (ret != _vIndexMap.end())
            {
                return ret->second;
            }
            else
            {
                throw invalid_argument("not exist vertex");
                return -1;
            }
        }

        void AddEdge(const V &src, const V &dst, const W &w)
        {

            size_t srcindex = GetVertexIndex(src);
            size_t dstindex = GetVertexIndex(dst);

            Edge *sd_edge = new Edge(w);
            sd_edge->_srcIndex = srcindex;
            sd_edge->_dstIndex = dstindex;
            sd_edge->_next = _linkTable[srcindex];
            _linkTable[srcindex] = sd_edge;

            //如果是无向图

            if (Direction == false)
            {

                Edge *ds_edge = new Edge(w);
                ds_edge->_srcIndex = dstindex;
                ds_edge->_dstIndex = srcindex;
                ds_edge->_next = _linkTable[dstindex];
                _linkTable[dstindex] = ds_edge;
            }
        }

    private:
        map<string, int> _vIndexMap;
        vector<V> _vertexs;        //顶点集合
        vector<Edge *> _linkTable; //边的集合
    };

    void TestGraph()
    {

        string a[] = {"zhangsan", "lisi", "wangwu", "zhaoliu"};
        Graph<string, int> g1(a, 4);
        g1.AddEdge("zhangsan", "lisi", 100);
        g1.AddEdge("zhangsan", "wangwu", 200);
        g1.AddEdge("wangwu", "zhaoliu", 30);
    }

}

int main()
{

    LinkTable::TestGraph();

    system("pause");
    return 0;
}