数据结构–字符串的KMP算法

朴素模式匹配算法：
一旦发现当前这个子串中某个字符不匹配，就只能转而匹配下一个子串(从头开始)

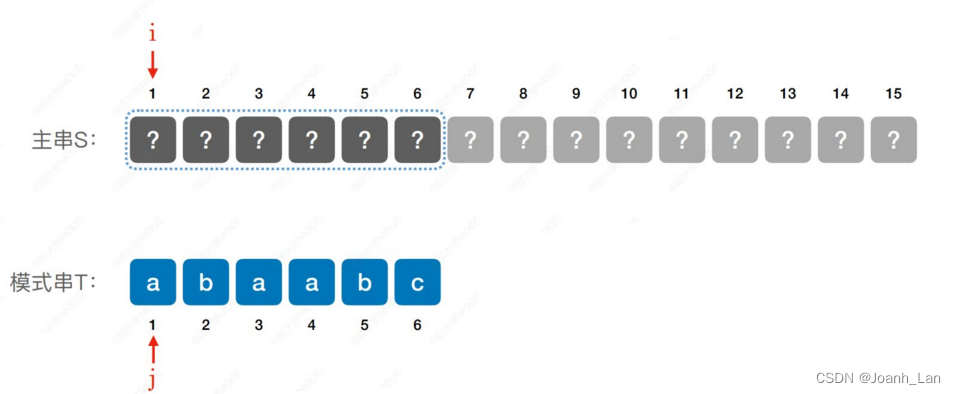
但我们可以知道：
$\color{red}不匹配的字符之前，一定是和模式串一致的$

我们可以利用这个信息进行优化查找，我们知道一定无法匹配的就无需再进行匹配操作了

我们可以发现：

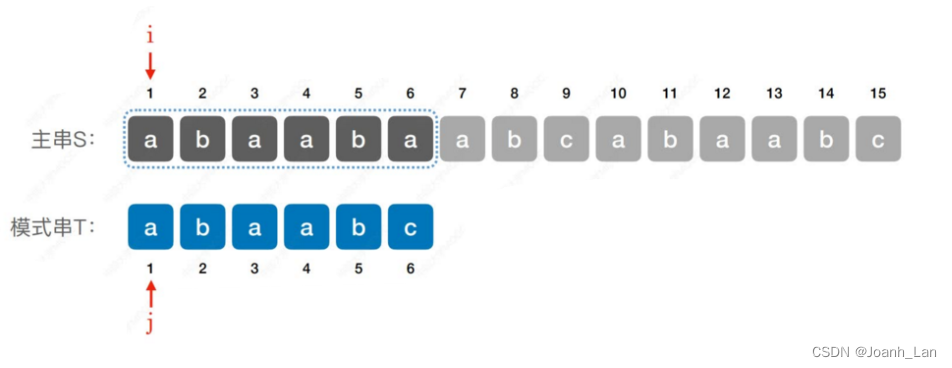
对于模式串T = ‘abaabc’
当 $\color{red}第6个$ 元素匹配失败时，可令主串指针 $\color{red}i不变$ ，模式串指针 $\color{red}j=3$
当 $\color{red}第5个$ 元素匹配失败时，可令主串指针 $\color{red}i不变$ ，模式串指针 $\color{red}j=2$
当 $\color{red}第4个$ 元素匹配失败时，可令主串指针 $\color{red}i不变$ ，模式串指针 $\color{red}j=2$
当 $\color{red}第3个$ 元素匹配失败时，可令主串指针 $\color{red}i不变$ ，模式串指针 $\color{red}j=1$
当 $\color{red}第2个$ 元素匹配失败时，可令主串指针 $\color{red}i不变$ ，模式串指针 $\color{red}j=1$
当 $\color{red}第1个$ 元素匹配失败时，匹配下一个相邻子串，令 $\color{red}j=0, i++, j++$

再来一个Eg：

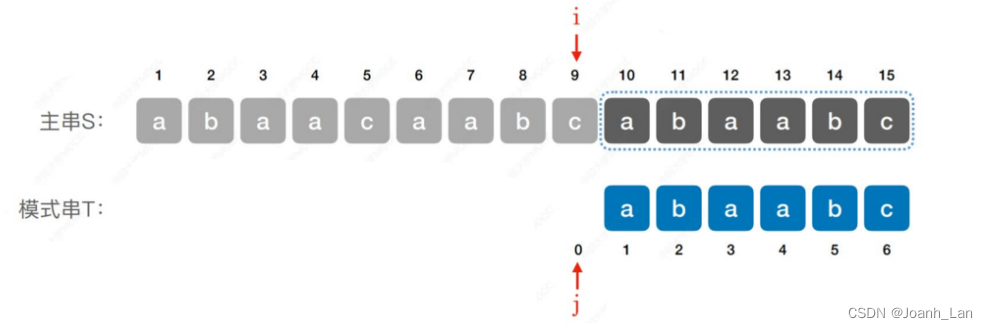
对于模式串T = 'abaabc' 当$\color{red}第6个$元素匹配失败时，可令主串指针$\color{red}i不变$，模式串指针$\color{red}j=3$ 当$\color{red}第5个$元素匹配失败时，可令主串指针$\color{red}i不变$，模式串指针$\color{red}j=2$ 当$\color{red}第4个$元素匹配失败时，可令主串指针$\color{red}i不变$，模式串指针$\color{red}j=2$ 当$\color{red}第3个$元素匹配失败时，可令主串指针$\color{red}i不变$，模式串指针$\color{red}j=1$ 当$\color{red}第2个$元素匹配失败时，可令主串指针$\color{red}i不变$，模式串指针$\color{red}j=1$ 当$\color{red}第1个$元素匹配失败时，匹配下一个相邻子串，令$\color{red}j=0, i++, j++$

代码实现

typedef struct
{
    char ch[15];
    int length;
}SString;

int Index_KMP(SString S, SString T, int next[])
{
    int i = 1, j = 1;
    while (i <= S.length && j <= T.length)
    {
        if (j == 0 || S.ch[i] == T.ch[j])
            i++, j++; //继续比较后继字符
        else
            j = next[j]; //模式串向右移动
    }
    if (j > T.length)
        return i - T.length;
    else
        return 0;
}