在学习机器学习或深度学习基础知识的同时训练模型是一个非常有指导性的过程。该数据集易于理解且格式适当，可供您使用。然而，当您走进现实世界并尝试解决行业或现实生活中的挑战时，数据集如果一开始就不存在，通常会很混乱。理解为什么你的模型并不简单。没有具体的步骤可以引导您找到答案。但是，存在某些工具可以让您调查并获得有关模型输出的更深入的见解。可视化是一种非常强大的工具，可以提供宝贵的信息。在这篇文章中，我将讨论两种非常强大的技术，它们可以帮助您在低维空间中可视化高维数据以发现趋势和模式，即 PCA 和 t-SNE。我们将采用基于 CNN 的示例，并在测试数据集中注入噪声来进行可视化研究。

1. 主成分分析（PCA）

1.1 概念

PCA 是一种探索性工具，通常用于将大型且复杂的数据集简化为更小、更容易理解的数据集。它通过进行正交线性变换来实现这一点，将数据变换到一个新的坐标系，该坐标系按主成分形式的方差内容排列，即您的高维相关数据被投影到具有线性独立基的较小空间中。第一个分量的方差最大，最后一个分量的方差最小。在原始空间中相关的特征在这个新的子空间中以线性独立或正交基向量表示。 [注：给定向量空间V的基集B包含的向量允许V中的每个向量被唯一地表示为这些向量的线性组合[2]。 PCA 的数学超出了本文的范围。]

您可以将这些组件用于很多事情，但在本文中，我将使用这些组件来可视化我们

通常从中获得的特征向量或嵌入中的模式2D/3D 空间中神经网络的倒数第二层。

2. t-分布式随机邻居嵌入（t-SNE）

t-distributed stochastic neighbour embedding (t-SNE)

2.1　t-sne定义

t-SNE 是一种强大的可视化技术，可以帮助发现低维空间中的数据模式。它是一种非线性降维技术。然而，与 PCA 不同的是，它涉及迭代优化，需要时间才能收敛，并且有一些参数可以调整。涉及两个主要步骤。首先，t-SNE 在高维对象对上构建概率分布，以便为相似的对象分配较高的概率，为不相似的对象分配较低的概率。相似度是基于某种距离（例如欧几里德距离）计算的。接下来，t-SNE 在低维空间中定义相似的概率分布，并最小化两个分布之间相对于空间中点的位置的 Kullback-Leibler 散度（KL 散度）。 KL 散度是一种统计工具，可让您衡量两个分布之间的相似性。当您使用一个分布来近似另一个分布时，它会为您提供丢失的信息。因此，如果 KL 散度最小化，我们就会发现一个分布，它是相似和不相似对象的高维分布的非常好的低维近似。这也意味着结果不会是唯一的，并且每次运行都会得到不同的结果。因此，在得出结论之前，最好多次运行 t-SNE 算法。

接下来，我将讨论我们将在本文中使用的分类数据集和架构。

3. 使用 CNN 进行 MNIST 分类

我想使用真实世界的数据集，因为我在最近的一个工作项目中使用了这种技术，但由于 IP 原因我无法使用该数据集。因此我们将使用著名的 MNIST 数据集 [4]。（好吧，尽管它现在已经成为一个玩具数据集，但它的多样性足以展示该方法。）

它总共由70,000张手写数字图像组成。这些样本分为 60,000 个训练样本和 10,000 个测试样本。这些是 28x28 灰度图像。下面显示了一些带有相应标签的随机样本。

在这里插入图片描述

3.1模型构建

我将使用一个小型 CNN 架构来执行分类并在 PyTorch 中构建它。架构如下图所示：

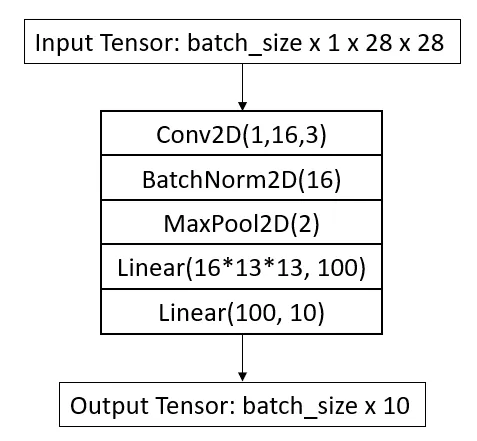
在这里插入图片描述
它由一个带有 16 个滤波器的 conv2d 层和两个全连接层线性层组成。网络为每个图像输出 10 个值。我应用了最大池化来减少特征维度。网络参数汇总如下所示。

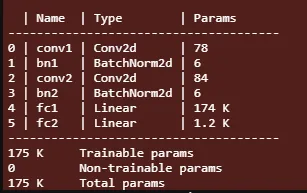
在这里插入图片描述
我们看到，即使是这个微小的网络也有 175k 个参数。这里需要注意的是，与全连接层相比，CNN 层的网络参数非常少。这些线性层还对网络的输入大小引入了限制，因为它是针对 28x28 输入计算的，并且会根据其他输入大小更改其尺寸。这就是为什么我们不能使用具有完全连接层的预训练 CNN 模型来处理与训练期间使用的尺寸不同的输入。除了最后一层之外，我在每一层之后都应用了 ReLU 激活。

由于 PyTorch 中的 cross_entropy 损失需要原始 logits。它在内部应用了softmax。因此，在使用该特定功能时请记住这一点。

3.2模型训练

对于训练，我使用具有默认设置的 Adam 优化器，模型经过 20 个 epoch 的训练，并基于最低的验证损失保留最佳模型。随着训练的进行，我通过查看训练和验证指标观察到了过度拟合的趋势。我认为向您展示它可能是个好主意。

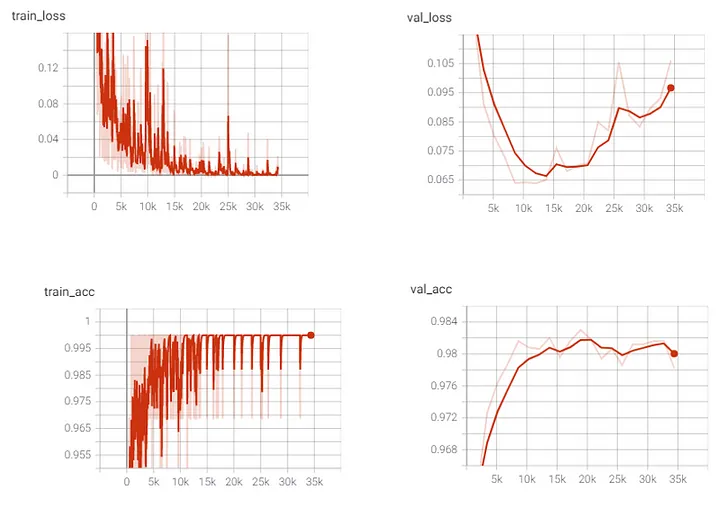
在这里插入图片描述

3.3 loss　与精度

在整个训练过程中，我们看到训练损失呈下降趋势，而训练准确率呈上升趋势。这意味着我们的模型复杂性足以满足我们的训练数据集。对于验证损失，我们看到直到第 7 纪元（步骤 14k）为止损失都在减少，然后损失开始增加。验证准确性有所增加，但到最后也开始下降。要了解有关偏差方差权衡、过拟合和欠拟合的更多信息，您可以阅读这篇文章：

https://towardsdatascience.com/bias-variance-trade-off-7b4987dd9795?sk=38729126412b0dc94ca5d2a9494067b7

4. 特征可视化

现在我们将继续本文的核心，即特征向量或嵌入的可视化。

4.1　载入库函数

我不会解释训练代码。那么让我们从可视化开始。我们需要导入一些库。我在脚本中使用 PyTorch Lightning，但代码适用于任何 PyTorch 模型。

import matplotlib.pyplot as plt
import numpy as np
import torch
from matplotlib import cm
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.datasets import MNIST
from visualization import ANN
%matplotlib widget

4.2　加载模型

我们加载经过训练的模型，将其发送到 GPU 并将其置于评估模式。将模型放入 eval 中非常重要，因为它将适当地设置 BatchNorm、Dropout 等层，以便在推理过程中正常运行。

model = ANN.load_from_checkpoint("\lightning_logs\version_0\checkpoints\epoch=4-step=8594.ckpt")
model = model.cuda()
model.eval()

4.3　加入噪声

接下来，我们加载 MNIST 数据集并在数据集中注入一些噪声样本。

transform = transforms.Compose([transforms.ToTensor()])
data = MNIST(".", train=False, download=True, transform=transform)
test_sample = torch.unsqueeze(data.data[:32].clone().cuda(),1).float()
plt.figure()
for i in range(32):
    plt.subplot(4,8,i+1)
    plt.imshow(data.data[i], cmap='gray')
    plt.axis('off')
    plt.title(data.targets[i].item())
np.random.seed(19)
num_wrong_samples = 1000
random_indices = np.random.uniform(0, 10000, num_wrong_samples).astype(np.uint8)
outlier_list = []
for i in range(num_wrong_samples):
    outlier = np.random.uniform(0,255, (28,28)).astype(np.uint8)
    outlier_list.append(outlier)
plt.figure()
plt.imshow(outlier)
for idx in range(num_wrong_samples):
    data.data[random_indices[idx]] = torch.ByteTensor(outlier_list[idx])
    data.targets[random_indices[idx]] = 10
dataloader = DataLoader(data, batch_size=32)

注入的噪声看起来像这样
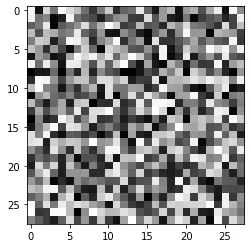
在这里插入图片描述

4.4　返回预测张量

所以我们知道模型必须吐出一些类，但这对于这些样本来说是垃圾。这是使用深度学习模型的问题之一，如果遇到分布外的数据，则很难预测模型会预测什么。推广到看不见的数据总是存在挑战。我定义了模型，使其返回嵌入张量以及最终预测张量。这样可以轻松访问，而无需更改 PyTorch 中的前向钩子。

4.5　输出中间层向量

但是，如果您确实发现自己想要访问预训练模型的中间层的输出，您可以使用以下代码来注册前向挂钩。

model = YourNeuralNetwork()
model.eval()
model = model.cuda()
# Define your output variable that will hold the output
out = None
# Define a hook function. It sets the global out variable equal to the
# output of the layer to which this hook is attached to.
def hook(module, input, output):
    global out
    out = output
    return None
# Your model layer has a register_forward_hook that does the registering for you
model.drop_6.register_forward_hook(hook)

# Then you just loop through your dataloader to extract the embeddings
embeddings = np.zeros(shape=(0,2048))
labels = np.zeros(shape=(0))
for x,y in iter(dataloader):
    global out
    x = x.cuda()
    model(x)
    labels = np.concatenate((labels,y.numpy().ravel()))
    embeddings = np.concatenate([embeddings, out.detach().cpu().numpy()],axis=0)

4.6　提取特征向量

MNIST数据集的预测代码如下。我们只需循环数据集，通过网络进行前向传播，提取嵌入，并将其存储在嵌入张量中。

test_imgs = torch.zeros((0, 1, 28, 28), dtype=torch.float32)
test_predictions = []
test_targets = []
test_embeddings = torch.zeros((0, 100), dtype=torch.float32)
for x,y in dataloader:
    x = x.cuda()
    embeddings, logits = model(x)
    preds = torch.argmax(logits, dim=1)
    test_predictions.extend(preds.detach().cpu().tolist())
    test_targets.extend(y.detach().cpu().tolist())
    test_embeddings = torch.cat((test_embeddings, embeddings.detach().cpu()), 0)
    test_imgs = torch.cat((test_imgs, x.detach().cpu()), 0)
test_imgs = np.array(test_imgs)
test_embeddings = np.array(test_embeddings)
test_targets = np.array(test_targets)
test_predictions = np.array(test_predictions)

4.7　检查

为了进行健全性检查，我绘制了几个样本输入测试点的输出预测。
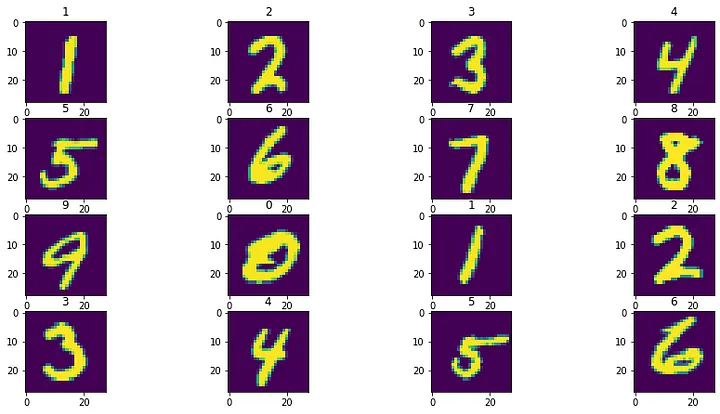
在这里插入图片描述

4.8　可视化输出结果

该模型似乎按预期工作，预测标签显示在每个子图的顶部。最后，我们可以进行 t-SNE 和 PCA 投影来看到一些漂亮的视觉效果。我使用 scikit-learn 来实现这些算法。

# Create a two dimensional t-SNE projection of the embeddings
tsne = TSNE(2, verbose=1)
tsne_proj = tsne.fit_transform(test_embeddings)
# Plot those points as a scatter plot and label them based on the pred labels
cmap = cm.get_cmap('tab20')
fig, ax = plt.subplots(figsize=(8,8))
num_categories = 10
for lab in range(num_categories):
    indices = test_predictions==lab
    ax.scatter(tsne_proj[indices,0],tsne_proj[indices,1], c=np.array(cmap(lab)).reshape(1,4), label = lab ,alpha=0.5)
ax.legend(fontsize='large', markerscale=2)
plt.show()

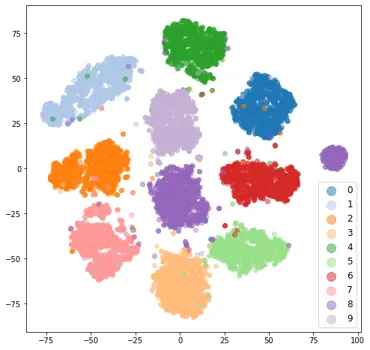
训练后的模型嵌入的结果图如下所示。正如预期的那样，我们看到了 11 个漂亮的簇。该模型预测所有噪声样本为 8 个。我们在这些噪声图像的图表最右侧看到紫色簇。这是一种异常现象，应在实际数据集调查中进一步调查此类异常或异常值。您可以使用 x,y 位置来获取嵌入的索引并将其映射到图像索引。这将告诉您这些样本有什么问题。

在这里插入图片描述

4.9　 3D t-SNE

我还计算了 3D t-SNE 投影，只是为了表明这样做同样容易。

tsne = TSNE(3, verbose=1)
tsne_proj = tsne.fit_transform(test_embeddings)
cmap = cm.get_cmap('tab20')
num_categories = 10
for lab in range(num_categories):
    indices = test_predictions == lab
    ax.scatter(tsne_proj[indices, 0],
               tsne_proj[indices, 1],
               tsne_proj[indices, 2],
               c=np.array(cmap(lab)).reshape(1, 4),
               label=lab,
               alpha=0.5)
ax.legend(fontsize='large', markerscale=2)
plt.show()

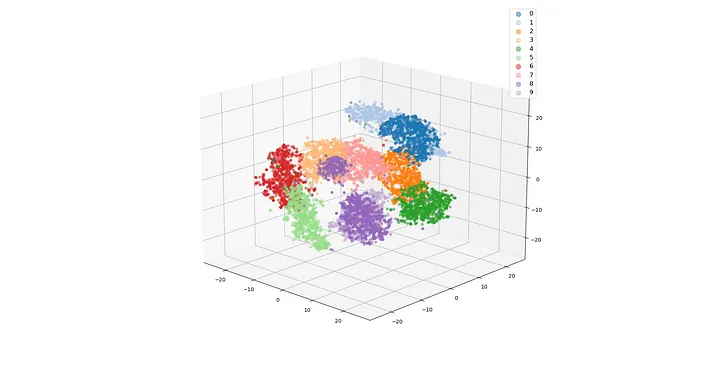
我们在 3D 投影中也观察到同样的情况。

在这里插入图片描述

4.10 PCA 可视化

对于 PCA，代码非常相似，但我们使用 PCA 类而不是 TSNE。我做了类似于 t-SNE 的 2d 和 3d 投影。但是，对于 PCA，您需要记住一个附加参数。这是解释的方差比率。这告诉您主成分捕获的数据的方差量。这些值越高，主成分就越能够显示低维空间中数据的变化。但较低的值表明只有 2 或 3 个组件不能很好地显示模式。


pca = PCA(n_components=2)
pca.fit(test_embeddings)
pca_proj = pca.transform(test_embeddings)
pca.explained_variance_ratio_
# array([0.16178058, 0.08613876], dtype=float32)

4.11 pca的不足

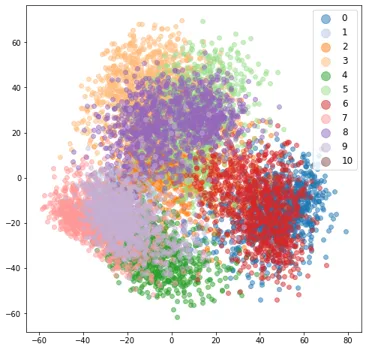
对于前两个主成分，仅捕获嵌入变化的 25%。我们确实看到了模式，但簇并不像 t-SNE 嵌入那么清晰。从 PCA 图中来看，异常值并不明显。不过，3D 图更好地显示了簇。这是因为 3 个分量捕获更多方差。因此，PCA 可视化的有效性取决于您的数据。

在这里插入图片描述

4.12　t-SNE 优势

在结束之前，我想再向您展示一张图，以让您清楚地了解 t-SNE 可视化的强大功能。作为实验，我使用具有随机权重的模型计算了嵌入，并绘制了 t-SNE 投影。为了正确地向您显示集群，我根据我们可用的实际标签对这些权重进行了颜色编码。我们看到 t-SNE 从未经训练的模型中提取的嵌入为我们提供了 11 个簇。

但您必须小心，t-SNE 可能会产生一些可能毫无意义的簇。另外重申一下我在引言中所说的，这些预测并不是独一无二的。因此，进行几次投影并验证是否在所有这些中都获得了相似的结果。

我们研究了 t-SNE 和 PCA 来可视化从神经网络获得的嵌入/特征向量。这些图可以向您显示数据中的异常值或异常值，可以进一步研究这些异常值以了解为什么会发生这种行为。这些方法的计算时间随着样本的增加而增加，因此请认识到这一点。感谢您的阅读，希望您喜欢阅读这篇文章。

代码可在此处获取：https://github.com/msminhas93/embeddings-visualization/blob/main/README.md