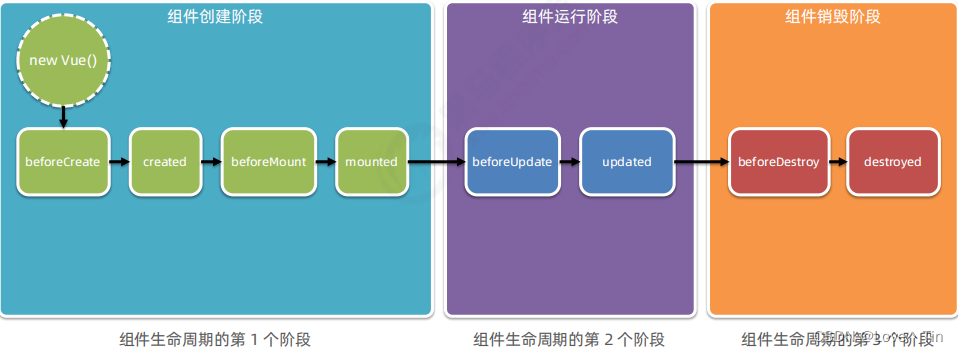
1 知识框架

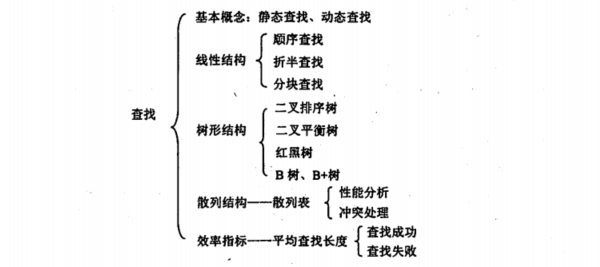
2 顺序查找和折半查找

2.1 顺序查找

1.一般线性表的顺序查找
优点：数据存储没有要求，是否有序没有要求
缺点：当n比较大时，平均查找长度较大，效率低。
2.有序表的顺序查找
如果是有序的，不用比较完全表就能返回查找失败信息，能有效降低查找失败的平均查找长度。
例如数据升序排列，第k个数小于key，而k+1个数大于key，即可知道表中没有key元素，查找失败。

2.2折半查找

又称二分查找，只适用有序的顺序表。

int low = 0,high = array,length() - 1,mid;
while(low <= high)
{
	mid = (low + high) / 2;
	if(array[mid] == key)
		return mid;   //  返回查找成功的位置
	else if(array[mid] < key)
		{
			low = mid + 1;
		}
	else 
	{
		high = mid - 1;
	}
}
return -1;   // 查找失败

折半查找过程可用二叉树描述，称判定树。

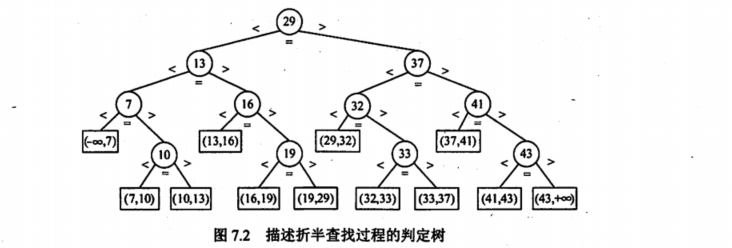
2.3 分块查找

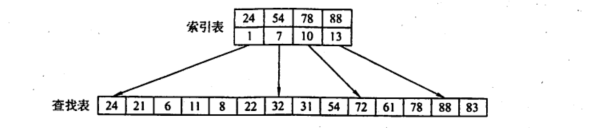
1.把查找表分为若干块，块内无序，块间要就前一块内最大值小于后一块内的所有值
2.构建索引表，含每个块的最大值和第一个元素的地址

3 树型查找

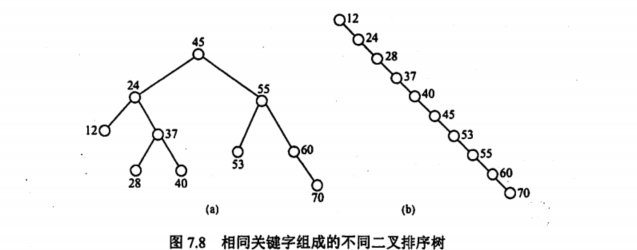
3.1 二叉排序树

1.二叉排序树的查找

while(T != NULL&& T -> data != key)
{
	if(key < T -> data)T = T -> lchild;
	else T = T -> rchild;
}

2.二叉排序树的插入

int insert(Tree &T,int key)
{
	if(T == NULL)
		{
			T = new BSTNode;
			T -> data = key;
			T ->lchild = T -> rchild = NULL;
			return 1;   // 插入成功
		}
	else if(k == T -> data) return -1;   //存在相同元素，插入失败
	else if(key < T ->data)
		return insert(T -> lchild,key);
	else if(key > T -> data)
		return insert(T -> rchild,key);
}

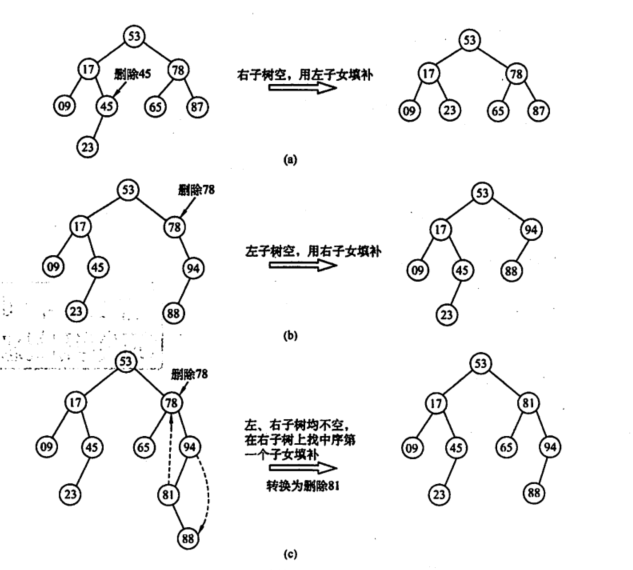
3.二叉树的删除
a.叶结点直接删除
b.删除结点有一颗子树，子树直接替代删除结点
c.删除结点有两颗子树，让删除的结点的直接后继或者前驱替代（中序遍历）

3.2 平衡二叉树

1.LL
(a)是插入结点前
（b） 插入结点在B结点的左子树
（c）将B右旋

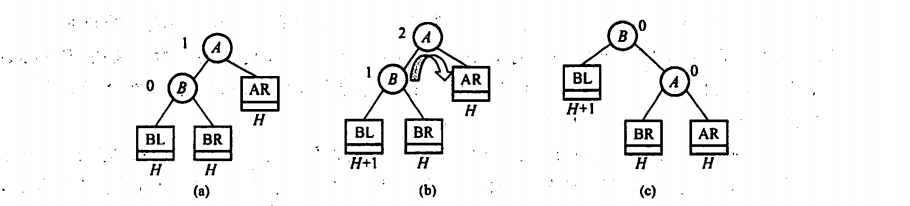
2.RR
与LL一样

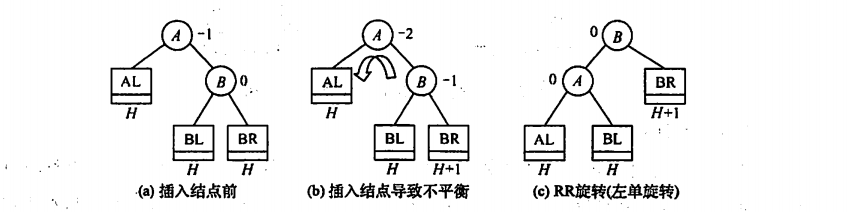
3.LR
在B结点的右子树插入结点导致不平衡
将B左旋A右旋

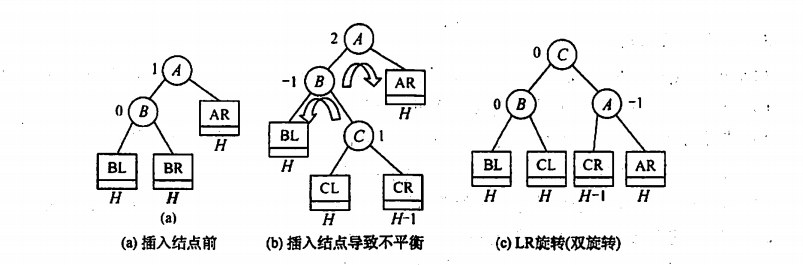
4.RL
与LR一样

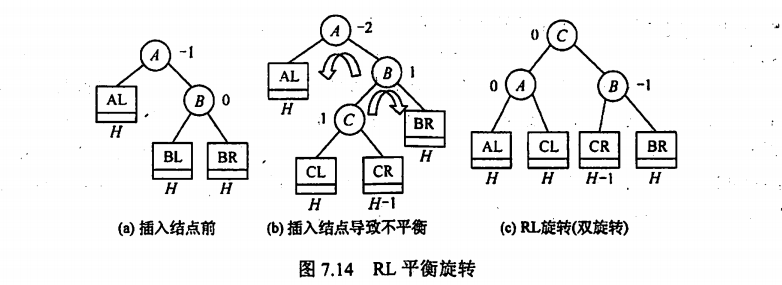
3.3 B树和B+树

3.3.1 B树

定义：
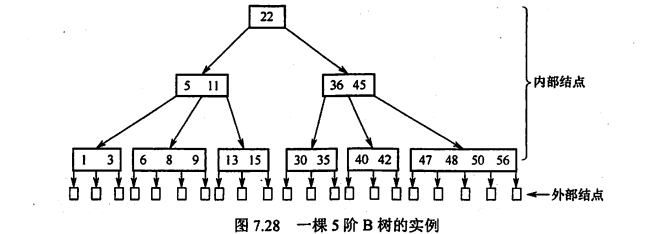
m阶B树是所有结点的平衡因子均等于0的m路平衡查找树
特点
1.每个结点最多m颗子树
2.关键字数范围m/2(向上取整) -1~ m-1
3.所以叶结点在同一层，且不存在，即查找失败的点

3.3.2 B+树

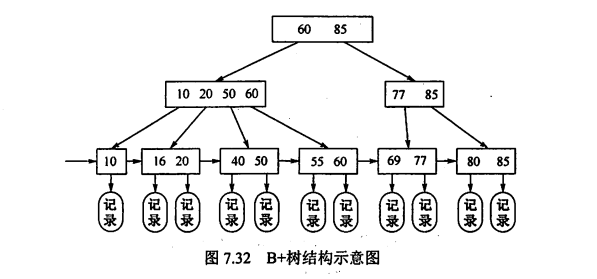
定义：所有分支结点中只包含子结点的一个最大关键字和指向子结点的指针

4 散列表

4.1 构造方法

1.直接定址法

给定函数：

H(key) = key || H(key) = a * key + b

优点：计算简单，不会产生冲突。适合关键字分布连续的。
如果分布不连续，产生的空位较多，会造成空间浪费的情况。

2.除留余数法

H(key) = key % p

关键在选p上，使关键字通过函数转换后映射在不同的地址上，尽可能减少冲突。

3.数字分析法
关键字为r进制数，选取数码分布较为均匀的若干位作为散列地址。
这种方法适合于已知的关键字集合。

4.平方取中法
取关键字的平方值的中间几位作为散列地址。
这种方法适用于关键字的每位取值都不够均匀或者小于散列地址所需的位数。

4.2 处理冲突的办法

1.开放地址法
发生冲突时，用Hi代表下一个找到的地址，通过下面的公式进行探测，知道Hi的地址不再冲突。

Hi = (H(key) + di) % m      // H(key) 为散列函数，di为增长序列，m表示线性表长

di的取法一共有四种

a.线性探测法
	di = 0,1,2,3,......,k   冲突发生时，顺序查看下一个地址是否空闲。
	缺点：
		可能导致第i个散列地址的元素存入第i + 1个地址，本该存在i + 1的存入i  +  2.。。。。。。从而造成元素堆积，大大降低元素查找效率。			
b.平方探测法
	di = 1²，-1²，2²，-2²，......，k²，-k²
	优点：一种较好的处理冲突的办法，可以避免堆积问题。
	缺点：不能探测到散列表上的所有单元，但至少能探测到一半以上。
c.双散列法 		
	di = Hash(key)
d.伪随机序列法
	di = 伪随机数。

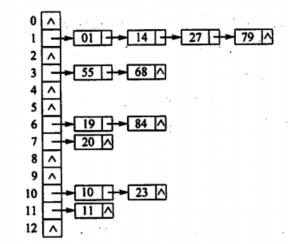
2.拉链法
将同义词存在同一个线性链表中，如图所示：

4.3性能分析

给定函数 H(key) = key % 13
关键字序列为：19,14,23,1,68,20,84,27,55,11,10,79
构造散列表得：
冲突使用线性探测解决

如果查找1，第一次 H1 = 1 % 13 = 1,1号位是14，则H2 = (1 + 1) % 13 = 2,L[2] = 1,则查找成功，得知查找元素1的次数是2
查找各关键字比较次数：

则平均查找长度ASL为：
ASL = （1 * 6 + 2 + 3 * 3 + 4 + 9) / 12 = 2.5