文章目录
- 1. 函数的嵌套调用和链式访问
- 1.1 嵌套调用
- 1.2 链式访问
- 2. 函数的声明和定义
- 2.1 函数定义
- 2.2 函数声明
- 2.3 函数的实际应用
- 3. 函数递归
- 3.1 什么是递归?
- 3.2 递归使用条件
- 3.3 递归的案例
- 3.4 递归的优缺点
- 4. 递归练习题
1. 函数的嵌套调用和链式访问
- 函数和函数之间是可以根据实际的需求进行组合的,也就是互相调用。
- 既然循环之间可以互相嵌套调用,那么函数当然也可以。
- 函数可以嵌套调用,但是不能嵌套定义。
1.1 嵌套调用
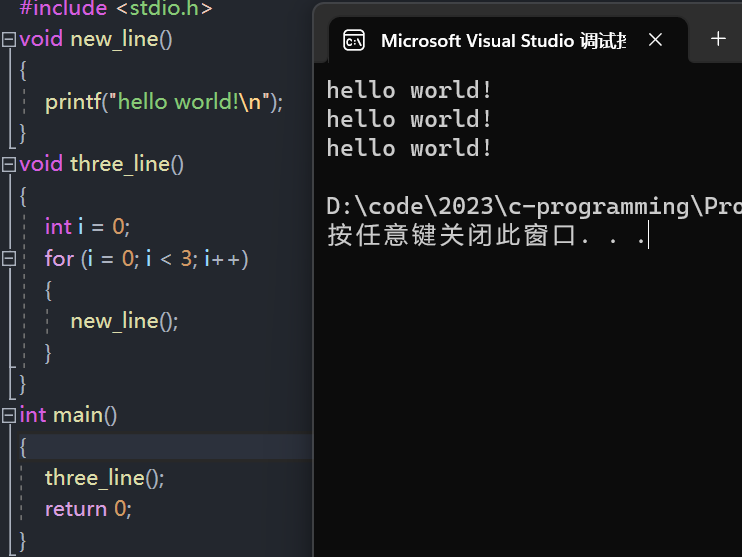
1. 函数只能嵌套调用
#include <stdio.h>
void new_line()
{
printf("hello world!\n");
}
void three_line()
{
int i = 0;
for (i = 0; i < 3; i++)
{
new_line();
}
}
int main()
{
three_line();
return 0;
}
2. 函数不能嵌套定义
- 函数之间都是平等的,函数之间只有互相调用的关系,但没有主仆关系。
1.2 链式访问
- 把一个函数的返回值作为另外一个函数的参数。
- 链式访问依赖的是函数的返回值。
- A 函数的返回值作了 B 函数的参数,这些函数之间就像个链条一样串了起来。
举个栗子
- 把 strlen 函数的返回值作为 printf 函数的参数。
#include <stdio.h>
#include <string.h>
int main()
{
printf("%d\n", strlen("abcdef"));
return 0;
}
经典链式访问题
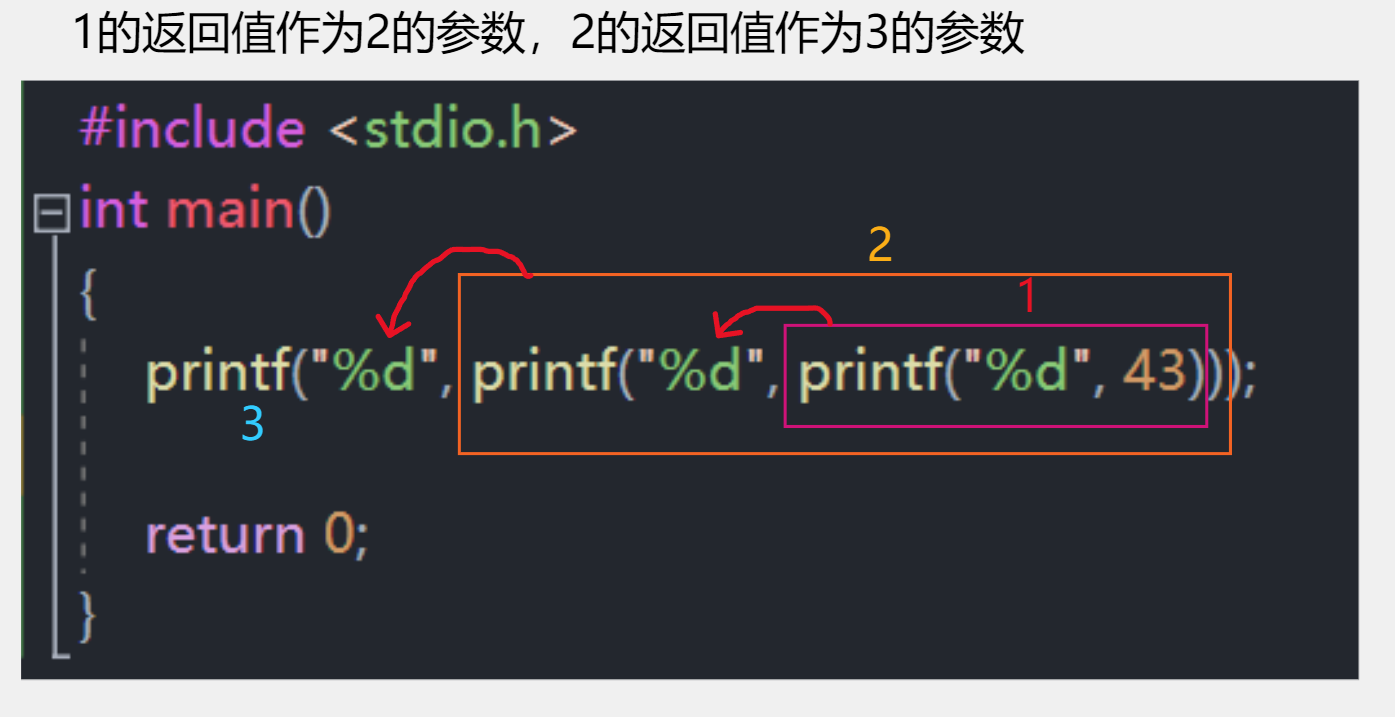
- 下面代码的结果是什么?
#include <stdio.h>
int main()
{
printf("%d", printf("%d", printf("%d", 43)));
return 0;
}
- printf :printf 函数的返回值是打印在屏幕上字符的个数。
- printf1 在屏幕上打印了 43 ,它的返回值是这一次在屏幕上打印的字符个数,也就是 2;
- printf2 接收到的 printf1 的返回值就是 2,在屏幕上打印一个字符 2,所以 printf2 的返回值就是在屏幕上打印的字符数量 1 了;
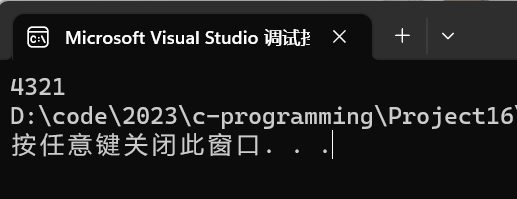
- printf3 接收到的返回值自然也就是 1了,所以这段代码的结果才会是 4321 这么一个看起来古怪的答案。
2. 函数的声明和定义
2.1 函数定义
- C 语言要求函数必须先定义,再调用,定义函数的格式如下:
类型名 函数名(参数列表)
{
函数体
}
- 类型名:就是函数的返回值,如果这个函数不准备返回任何数据,那么需要写上 void(void 就是无类型,表示没有返回值)。
- 函数名:就是函数的名字,一般我们根据函数实现的功能来命名,比如 print_C 就是“打印C”的意思,一目了然。
- 参数列表:指定了参数的类型和名字,如果这个函数没有参数,那么这个位置直接 void 即可。
- 函数体:就是指定函数的具体实现过程,是函数中最重要的部分。
举个栗子
//定义一个求两数之和的函数
int Add(int x, int y)
{
return x + y;
}
int main()
{
int a, b;
scanf("%d %d", &a, &b);
printf("%d\n", Add(a, b));
return 0;
}
2.2 函数声明
- 所谓声明(Declaration),就是告诉编译器我要使用这个函数,你现在没有找到它的定义不要紧,请不要报错,稍后我会把定义补上。
- 有时候,你可能会发现即使不写函数的声明,程序也是可以正常执行的。但如果你把函数的定义写在调用之后,那么编译器可能就会找不着北了。
- 函数的声明一般要用在头文件中
举个栗子
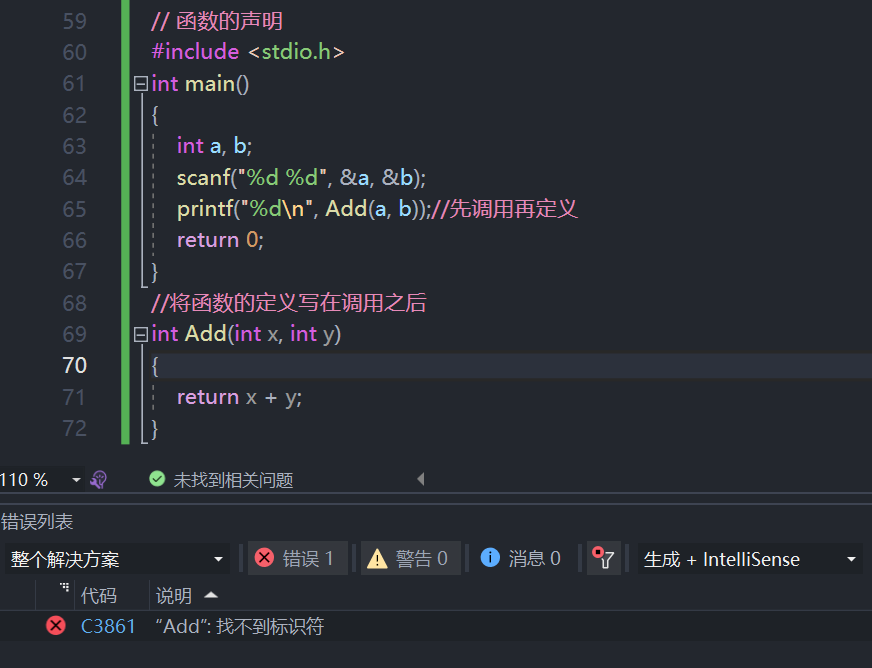
- 将函数的定义写在调用之后。
#include <stdio.h>
int main()
{
int a, b;
scanf("%d %d", &a, &b);
printf("%d\n", Add(a, b));//先调用再定义
return 0;
}
//将函数的定义写在调用之后
int Add(int x, int y)
{
return x + y;
}
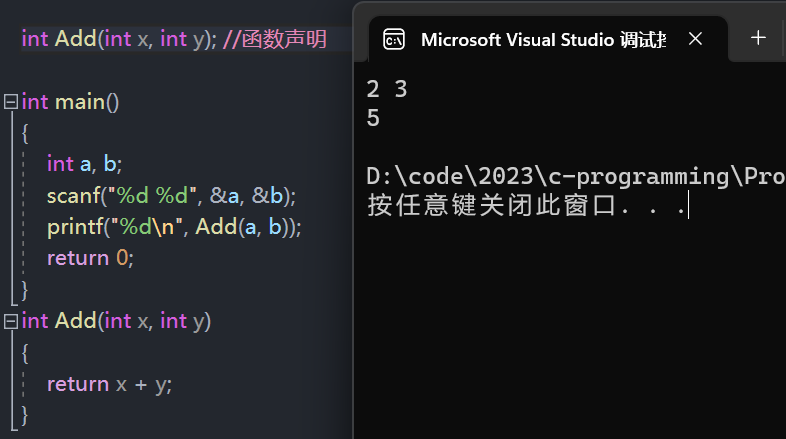
- 程序的编译是从上到下执行的,所以从原则上来说,函数必须先定义,再调用。
- 但在实际开发中,经常会在函数定义之前调用它们,这个时候就需要提前进行声明了。
函数声明格式
- 声明函数的格式非常简单,只需要去掉函数定义中的函数体再加上分号即可。
int Add(int x, int y);
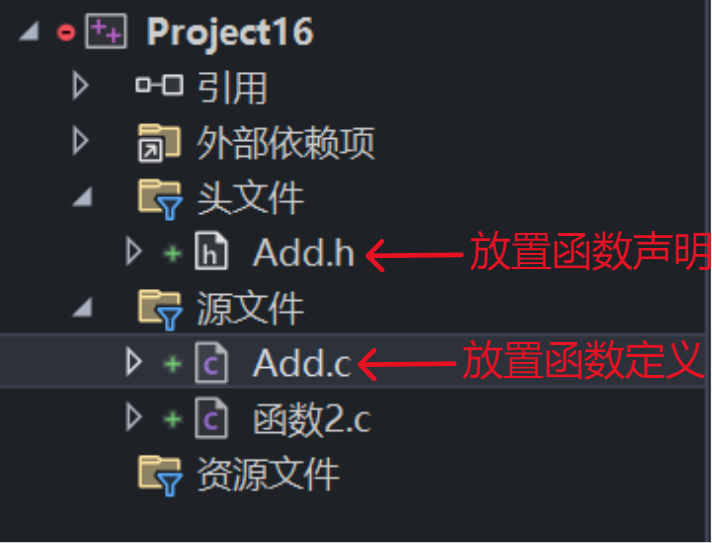
2.3 函数的实际应用
- 在实际工作的时候,是不会像上面那样将函数都写在同一个源文件底下的。
- 而是会把 Add 函数写成一个加法模块,在主函数中调用 Add 的头文件即可。各自分开写代码会让逻辑变得更清晰。
- 将函数的声明、定义以及调用写在不同的文件底下。
举个栗子
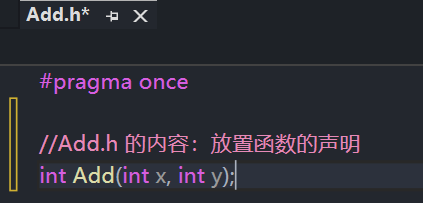
- .h 文件用于存放函数的声明,放置在头文件底下;
- .c 文件用于存放函数的实现,放置在源文件底下;
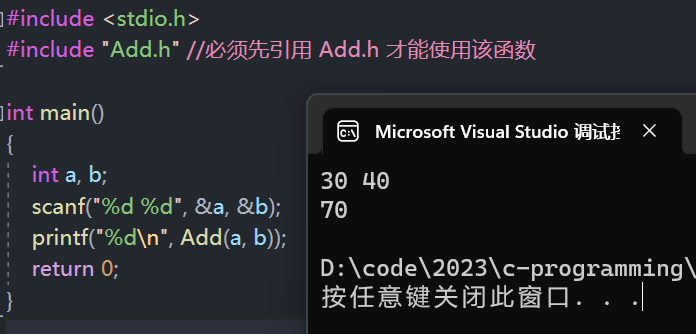
- 想使用 Add 函数的内容就得先引用 头文件 Add.h
#include <stdio.h>
#include "Add.h" //必须先引用 Add.h 才能使用该函数
int main()
{
int a, b;
scanf("%d %d", &a, &b);
printf("%d\n", Add(a, b));
return 0;
}
为何将函数的声明及定义放置在不同文件?
- 在初学编程的时候,觉得把所有的代码写到一个文件中最方便。
- 但是在工作中,假如所有的开发人员都把他们的函数写到同一个文件中,那这代码简直就没法看了。
- 不同的程序员在不同的文件底下写自己的函数,最后使用的时候直接引头文件即可。
3. 函数递归
- “ 从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事:‘从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事:……’ ”
- 这种自己套用自己的故事可以讲上一辈子,这个故事就很符合递归这个知识点。
3.1 什么是递归?
递归的概念
- 从原理上来说函数调用自身的行为称之为递归。
- 在函数内部可以调用其他函数,那么当然也可以调用函数本身。
- 递归的主要思考方式在于:把大事化小。
举个栗子
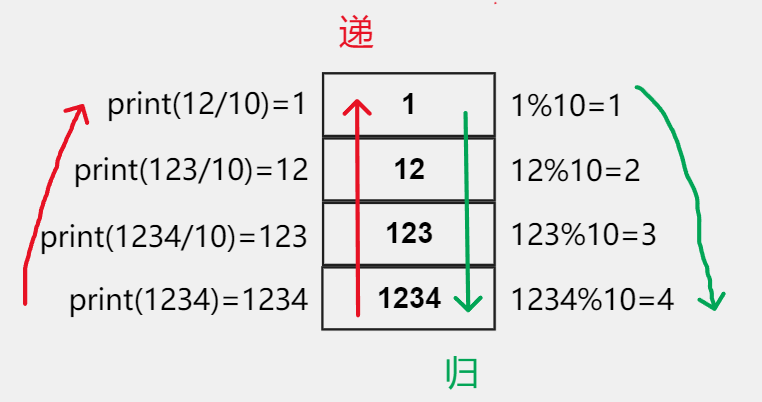
- 接受一个整型值(无符号),按照顺序打印它的每一位。
- 例如:输入:1234,输出 1 2 3 4。
#include <stdio.h>
void print(unsigned int n)
{
if (n > 9)//n > 9 就说明还有的拆
{
print(n / 10);//n /10 去掉最后一位数字
}
printf("%u ", n % 10);//n % 10 获得最后一位数字
}
int main()
{
unsigned int n;
scanf("%u", &n);
print(n);//此处为第一次调用 print 函数,
return 0;
}
-
前面几次调用 print 函数的时候其实是没有执行 n % 10 这一步的,而是直接开始下一次递进。
-
等到了最后 n 不大于 9 不满足执行递进的条件了,开始回归,n % 10 才能够执行。
- 递进完了之后再从最后一次递进所在的位置开始回归。
-
先递进,再回归,这就是 [递归]。
看到递归了吗?
递归的本质
- 递归的本质说白了就是递进,回归。
- 当达到递进的结束条件时,开始回归,回归是按照递进的轨迹一层一层的归来。
- 例如: 像我走到五楼时,到了顶层(递进结束条件),此时从五层开始一层一层的回归,直到回到一楼时结束递归。
3.2 递归使用条件
想使用递归有两个必要条件
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件。
3.3 递归的案例
1. 汉诺塔游戏
- 汉诺塔游戏要求将最左边柱子的圆盘借助中间柱子依次移动到最右边,要求每次只能移动一个圆盘,并且较大的圆盘必须在下方。
2. 谢尔斯宾基三角形
- 三角形里边填充有三角形,只要空间够大,它可以撑满整个宇宙,这就是谢尔斯宾及三角形。
3. 目录树的索引
- 后续开发程序可能会遇到目录访问的情况,需要逐层去访问目录,但是并不知道目录究竟有多少层,这时候使用递归就可以很好的解决这个问题。
3.4 递归的优缺点
1. 递归的优点
- 代码简介。
- 在树的前、中、后序遍历算法中,递归明显比循环要更好用。
2. 递归的缺点
-
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成栈溢出的后果。
-
递归中很多计算都是重复的,由于其本质是把一个问题分解成两个或者多个小问题,多个小问题存在相互重叠的部分,则存在重复计算,如斐波那契数列的递归实现。
4. 递归练习题
- 可能有小伙伴还是搞不太明白递归到底是怎么一回事,在这篇递归练习题中,我会详细讲解递归的具体:https://editor.csdn.net/md/?articleId=131504627