文章目录
- 知识准备
- 例题
- 543. 二叉树的直径
- 124. 二叉树中的最大路径和
- 2246. 相邻字符不同的最长路径
- 相关题目练习
- 687. 最长同值路径 https://leetcode.cn/problems/longest-univalue-path/solution/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-524j4/
- 1617. 统计子树中城市之间最大距离 https://leetcode.cn/problems/count-subtrees-with-max-distance-between-cities/solution/tu-jie-on3-mei-ju-zhi-jing-duan-dian-che-am2n/⭐⭐⭐⭐⭐
- 方法1——枚举子集+树的直径
- Arrays.setAll()和Arrays.fill()
- 方法2——二进制枚举
- Integer.numberOfTrailingZeros()
- 解法3——枚举直径端点+乘法原理
- 思路
- 代码
- 2538. 最大价值和与最小价值和的差值 https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/⭐⭐⭐⭐⭐
知识准备
一般 dfs 内的逻辑是找这个子树内的最长路径, dfs 的返回值是这个子树内最长的那个从根节点开始的链。

回忆 104. 二叉树的最大深度 这道题目。
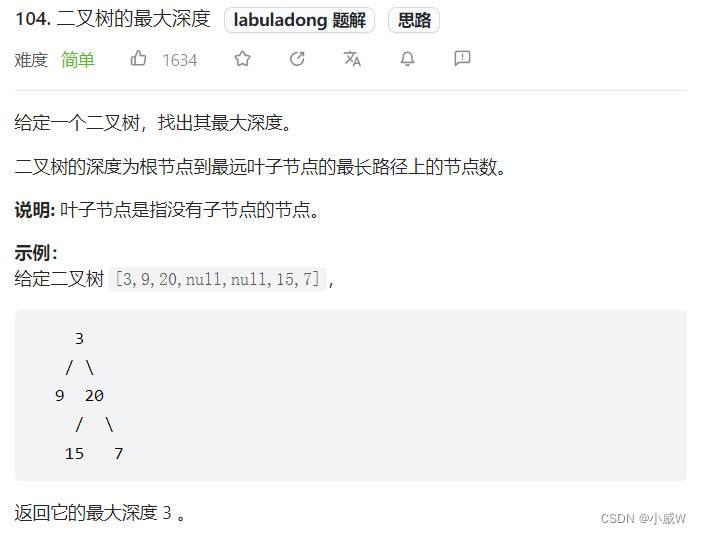
我们的做法是
整棵树的最大深度 = max(左子树的最大深度,右子树的最大深度) + 1
那么树的直径和最大深度之间是否有联系呢?
例题
543. 二叉树的直径
543. 二叉树的直径
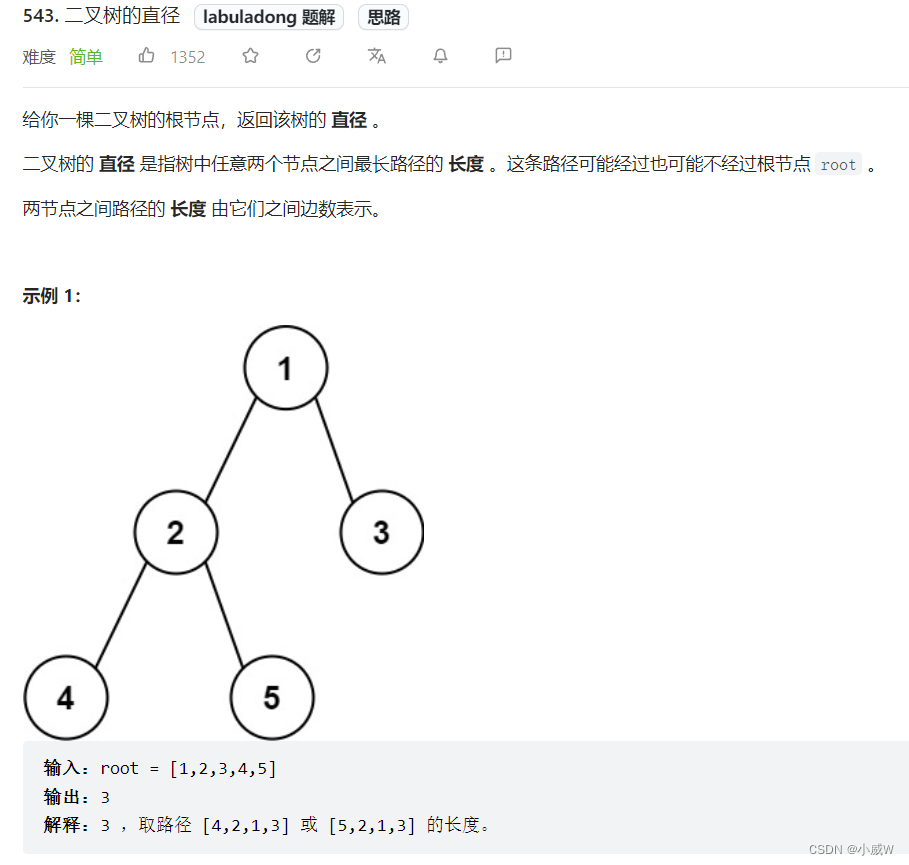
换个角度看直径:从一个叶子出发向上,在某个节点「拐弯」,向下到达另一个叶子。得到了由两条链拼起来的路径。(也可能只有一条链)
class Solution {
int ans = 0;
public int diameterOfBinaryTree(TreeNode root) {
dfs(root);
return ans - 1;
}
// 求节点的高度
public int dfs(TreeNode root) {
if (root == null) return 0;
int l = dfs(root.left), r = dfs(root.right);
ans = Math.max(ans, l + r + 1); // 更新答案
return 1 + Math.max(l, r);
}
}
这道题由于我本身就会做,所以没太感受到 dp 的味道。
我的解题思想是这样的:
以每个节点为拐点的直径长度就是 1 + 左叶子的高度 + 右叶子的高度,因此就用后序 dfs 不断得到各个节点的高度返回给它们的父节点,在这个过程中更新答案就好了。
124. 二叉树中的最大路径和
124. 二叉树中的最大路径和
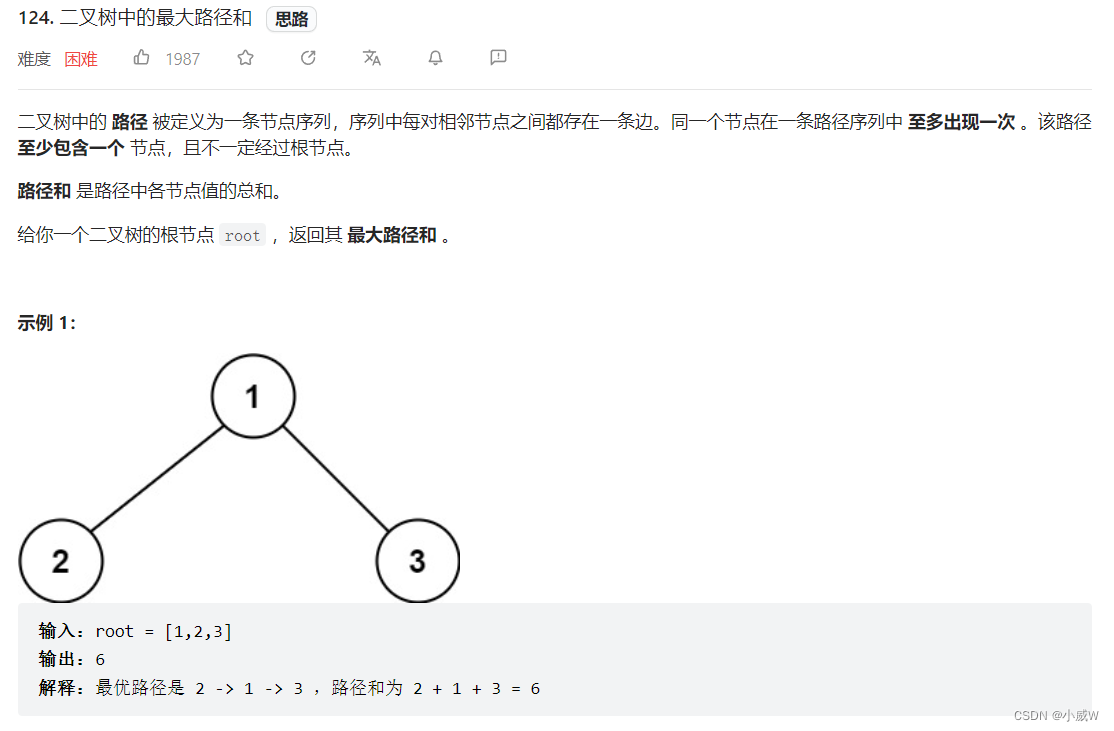
和 543. 二叉树的直径 这道题目的思路基本一致,区别在于子节点返回给父节点的值不再是节点的高度,而是从它到叶子节点的个节点值的最大路径总和。
class Solution {
int ans = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return ans;
}
public int dfs(TreeNode root) {
if (root == null) return 0;
int l = dfs(root.left), r = dfs(root.right);
ans = Math.max(ans, l + r + root.val);
return Math.max(0, Math.max(l, r) + root.val);
}
}
2246. 相邻字符不同的最长路径
2246. 相邻字符不同的最长路径

这道题目与上面题目的区别是:
- 这是一个多叉树,所以不能只计算两个子节点的返回值,而是所有子节点的返回值。
- 在计算答案时,需要确保当前节点和子节点的字符不相同。
其它思路与 543. 二叉树的直径 类似。
class Solution {
String s;
int ans = 1;
List<List<Integer>> childs = new ArrayList();
public int longestPath(int[] parent, String s) {
this.s = s;
int n = parent.length;
for (int i = 0; i < n; ++i) childs.add(new ArrayList());
// 用列表记录每个节点的所有子节点
for (int i = 1; i < n; ++i) {
childs.get(parent[i]).add(i);
}
dfs(0);
return ans;
}
public int dfs(int rootId) {
char ch = s.charAt(rootId);
int mxl1 = 0, mxl2 = 0; // 分别记录到子节点的最大高度和第二大高度
for (int i: childs.get(rootId)) {
int mxL = dfs(i);
if (ch != s.charAt(i)) {
if (mxL > mxl1) {
mxl2 = mxl1;
mxl1 = mxL;
} else if (mxL > mxl2) mxl2 = mxL;
}
}
ans = Math.max(ans, 1 + mxl1 + mxl2); // 答案是路径和
return 1 + mxl1; // 返回值是节点最大高度
}
}
相关题目练习
687. 最长同值路径 https://leetcode.cn/problems/longest-univalue-path/solution/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-524j4/
https://leetcode.cn/problems/longest-univalue-path/solution/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-524j4/
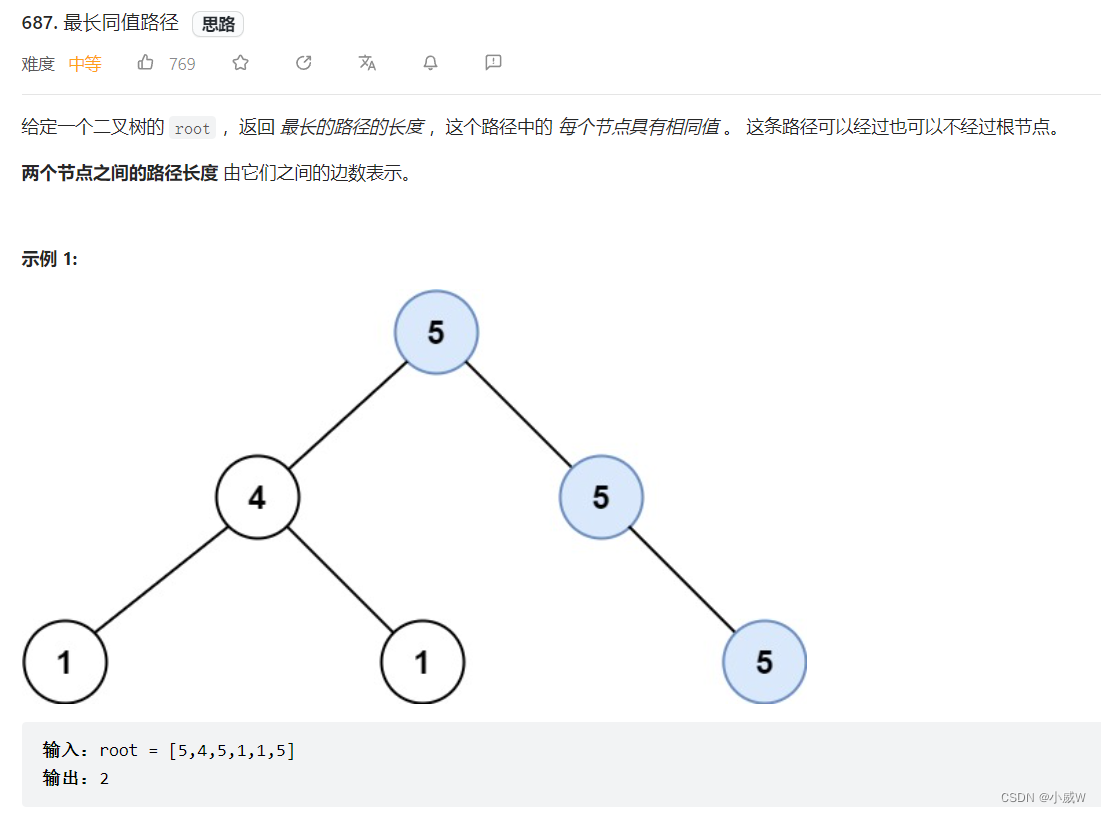
这道题目要求 当前节点和子节点的数值相同时 才可以选择。
class Solution {
int ans = 1;
public int longestUnivaluePath(TreeNode root) {
dfs(root);
return ans - 1; // 返回的是边数,所以是节点数-1
}
public int dfs(TreeNode root) {
if (root == null) return 0;
int l = dfs(root.left), r = dfs(root.right);
// 如果当前节点和子节点的数值不相同,那就不能选对应的子节点
if (l != 0 && root.val != root.left.val) l = 0;
if (r != 0 && root.val != root.right.val) r = 0;
ans = Math.max(ans, 1 + l + r); // 更新答案
return 1 + Math.max(l, r); // 返回值
}
}
1617. 统计子树中城市之间最大距离 https://leetcode.cn/problems/count-subtrees-with-max-distance-between-cities/solution/tu-jie-on3-mei-ju-zhi-jing-duan-dian-che-am2n/⭐⭐⭐⭐⭐
https://leetcode.cn/problems/count-subtrees-with-max-distance-between-cities/solution/tu-jie-on3-mei-ju-zhi-jing-duan-dian-che-am2n/

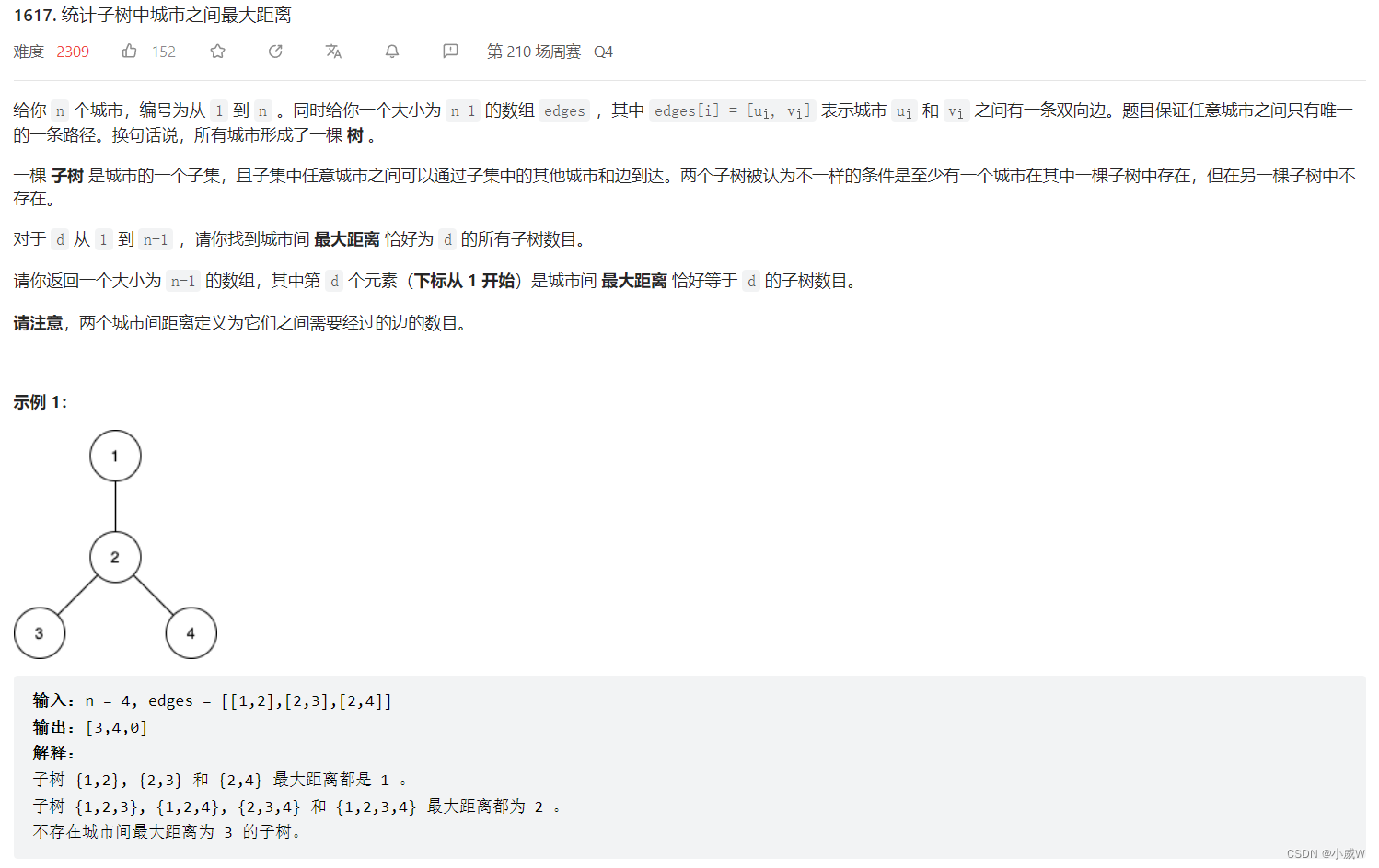
方法1——枚举子集+树的直径
使用回溯枚举整个城市的所有子集,
分别计算各个子集作为树的时候,它的直径是多少。
class Solution {
List<Integer>[] g; // 记录各个节点相邻的所有节点
int n, diameter;
boolean[] inSet, vis; // inSet记录子集中的节点,vis记录求直径时遍历到的节点
int[] ans;
public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
this.n = n;
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<Integer>());
// 建树
for (int[] edge: edges) {
int x = edge[0] - 1, y = edge[1] - 1;
g[x].add(y);
g[y].add(x);
}
inSet = new boolean[n];
ans = new int[n - 1];
dfs(0);
return ans;
}
public void dfs(int i) {
if (i == n) {
diameter = 0; // 计算之前先归零
// 计算当前子集树的直径
for (int v = 0; v < n; ++v) {
if (inSet[v]) { // 找到了一个在子集中的节点
vis = new boolean[n];
get(v); // 计算直径
break; // 只需要算一次就够了(从树中任意一个节点开始算都能算出相同的结果)
}
}
if (diameter > 0 && Arrays.equals(vis, inSet)) ans[diameter - 1]++;
return;
}
// 不选i
dfs(i + 1);
// 选i
inSet[i] = true;
dfs(i + 1);
inSet[i] = false;
}
public int get(int x) {
vis[x] = true;
int mxLen = 0; // 记录已经枚举过的分支的最大长度
for (int y: g[x]) {
if (!vis[y] && inSet[y]) {
int ml = get(y) + 1; // 当前枚举的分支的最大长度
diameter = Math.max(diameter, ml + mxLen); // 更新答案
mxLen = Math.max(mxLen, ml); // 更新当前枚举过的分支的最大长度
}
}
return mxLen; // 返回当前分支的最大长度
}
}
Q:为什么需要判断 if (diameter > 0 && Arrays.equals(vis, inSet)) ans[diameter - 1]++;
A:因为当 inSet 中的元素数量只有 0 个或者 1 个的时候,经过遍历同样 vis 和 inSet 会变得相同,但此时显然 diameter = 0,不符合题意。
Arrays.setAll()和Arrays.fill()
Arrays.setAll(g, e -> new ArrayList<Integer>()); 不能使用 Arrays.fill(g, new ArrayList()); ,因为 Arrays.fill() 进去的各个下标对应的其实是同一个列表,而不是像 setAll 那样每个位置创建了一个新列表。
方法2——二进制枚举
相当于方法1的优化,即是用二进制表示集合/布尔数组。
二进制从低到高第 i 位为 1 表示 i 在集合中,为 0 表示 i 不在集合中,例如集合 {0,2,3} 对应的二进制数为
110
1
(
2
)
1101 _{(2)}
1101(2)
class Solution {
private List<Integer>[] g;
private int mask, vis, diameter;
public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0] - 1, y = e[1] - 1; // 编号改为从 0 开始
g[x].add(y);
g[y].add(x); // 建树
}
var ans = new int[n - 1];
// 二进制枚举
for (mask = 3; mask < 1 << n; ++mask) {
if ((mask & (mask - 1)) == 0) continue; // 需要至少两个点
vis = diameter = 0;
dfs(Integer.numberOfTrailingZeros(mask)); // 从一个在 mask 中的点开始递归
if (vis == mask) ++ans[diameter - 1];
}
return ans;
}
// 求树的直径
private int dfs(int x) {
vis |= 1 << x; // 标记 x 访问过
int maxLen = 0;
for (int y : g[x])
if ((vis >> y & 1) == 0 && (mask >> y & 1) == 1) { // y 没有访问过且在 mask 中
int ml = dfs(y) + 1;
diameter = Math.max(diameter, maxLen + ml);
maxLen = Math.max(maxLen, ml);
}
return maxLen;
}
}
Q:为什么 if (vis == mask) ++ans[diameter - 1]; 不需要判断 diameter 的大小了。
A:因为 mask 确保了其中至少有两个点。(如果两个点不在一个树中,那么 vis 和 mask 也不会相等)
Integer.numberOfTrailingZeros()
Java中的Integer.numberOfTrailingZeros()方法是用来返回指定int值的二进制补码表示中最低位(最右边或最不重要的“1”位)后面跟着的零位的个数。如果指定的值在其二进制补码表示中没有一 位,也就是说它等于零,那么它返回32。
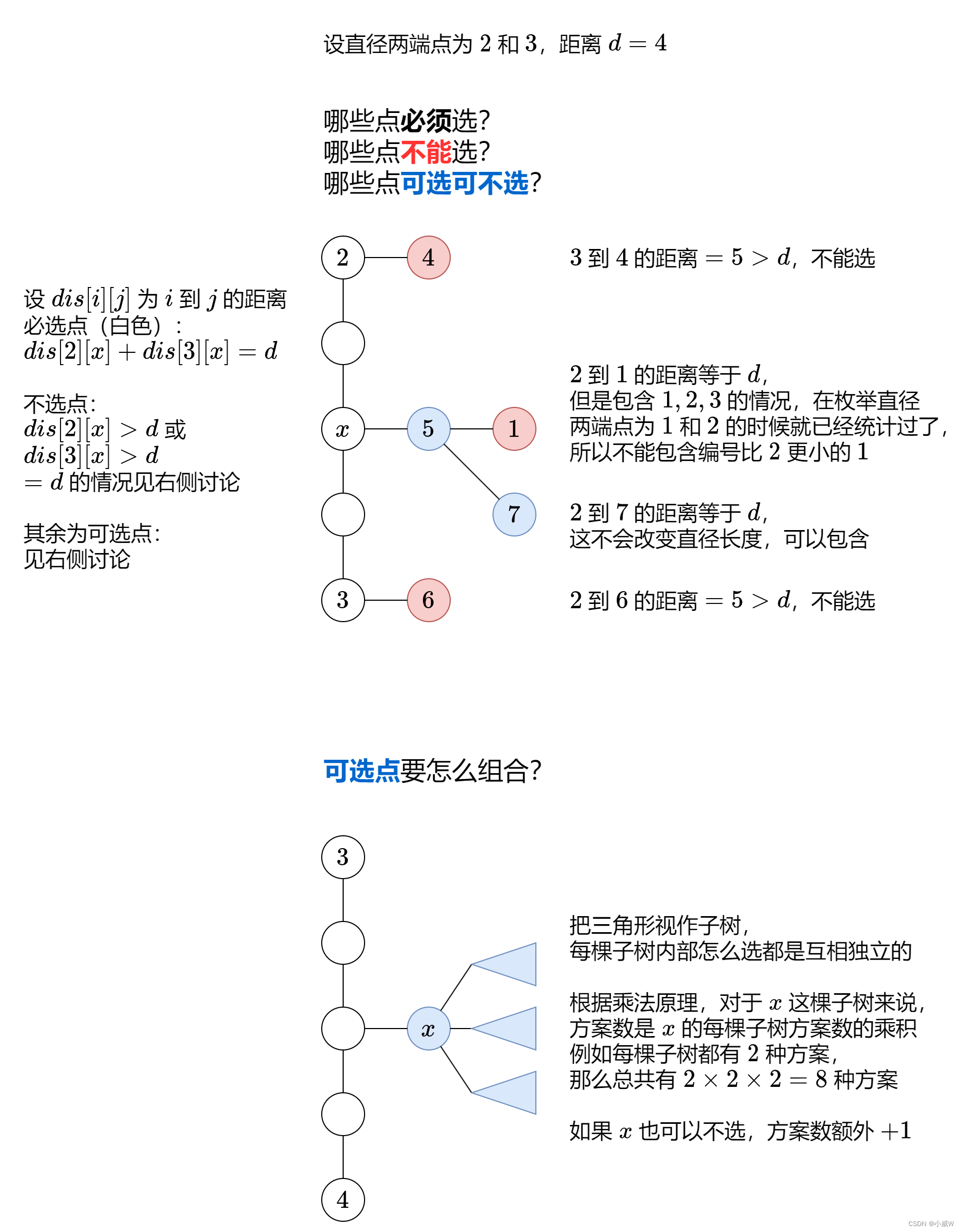
解法3——枚举直径端点+乘法原理
思路
暴力枚举 i 和 j 作为直径的两个端点 ,那么从 i 到 j 的这条简单路径是直径,这上面的每个点都必须选。
还有哪些点是可以选的?
为了计算树上任意两点的距离 dis,枚举 i 作为树的根,计算 i 到其余点的距离。这通常用 BFS 来做,但是对于树来说,任意两点的简单路径是唯一的,所以 DFS 也可以。
那么通过 n 次 DFS,就可以得到树上任意两点的距离了。
代码
class Solution {
List<Integer>[] g;
int[][] dis;
public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList());
for (int[] edge: edges) {
int x = edge[0] - 1, y = edge[1] - 1;
g[x].add(y);
g[y].add(x);
}
dis = new int[n][n];
for (int i = 0; i < n; ++i) dfs(i, i, -1); // 计算i到其余各点的距离
int[] ans = new int[n - 1];
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
// 加上从i到j的方案数
ans[dis[i][j] - 1] += dfs2(i, j, dis[i][j], i, -1);
}
}
return ans;
}
public void dfs(int i, int x, int father) {
for (int y: g[x]) {
if (y != father) {
dis[i][y] = dis[i][x] + 1;
dfs(i, y, x);
}
}
}
public int dfs2(int i, int j, int d, int x, int father) {
int cnt = 1;
for (int y: g[x]) {
if (y != father &&
(dis[i][y] < d || (dis[i][y] == d && y > j)) &&
(dis[j][y] < d || (dis[j][y] == d && y > i))) {
cnt *= dfs2(i, j, d, y, x); // 每棵子树互相独立,采用乘法原理
}
}
// != d表示x不是从i到j的最短路径上的节点,可以贡献方案
if (dis[i][x] + dis[j][x] != d) ++cnt;
return cnt;
}
}
时间复杂度是 O ( n 3 ) O(n^3) O(n3)
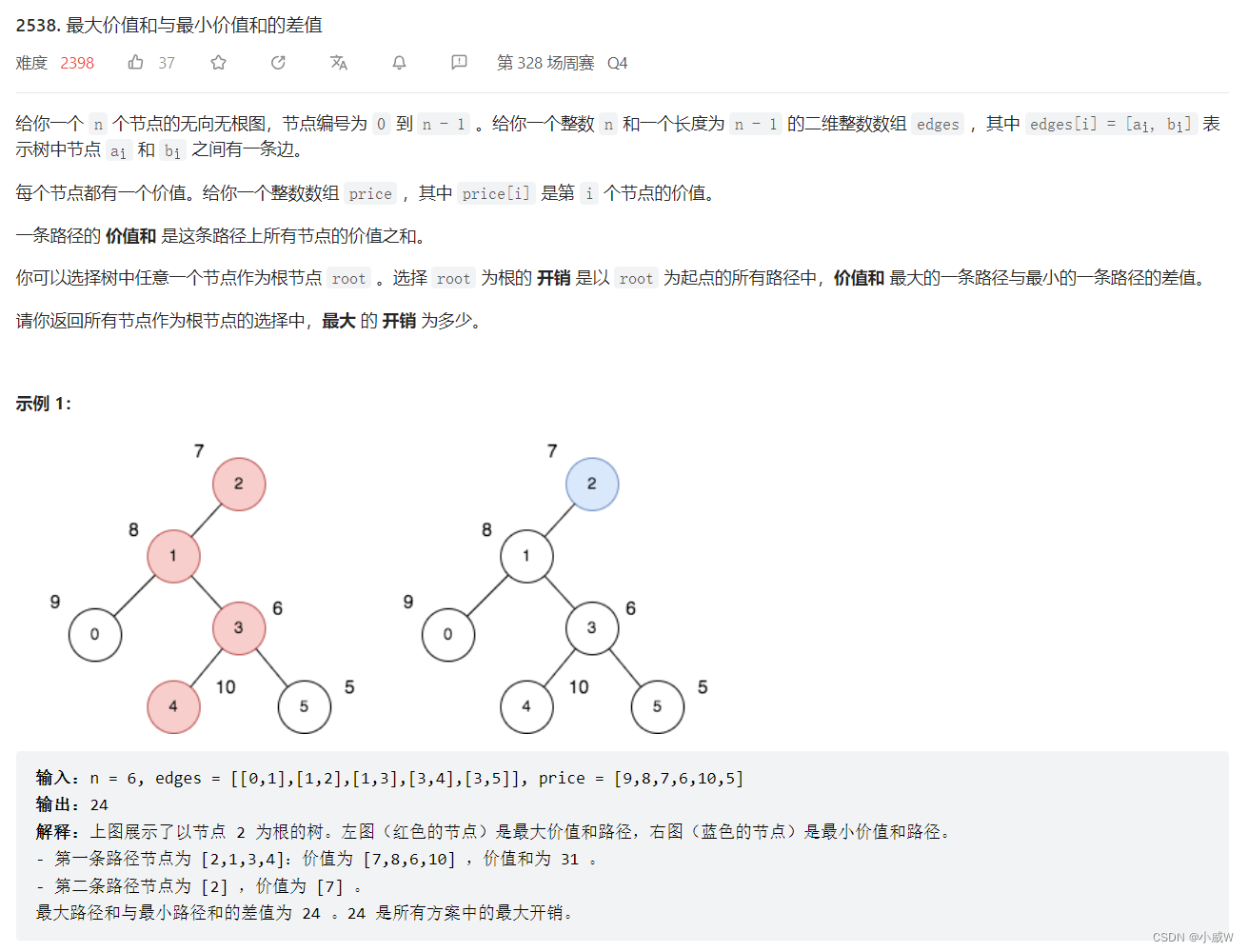
2538. 最大价值和与最小价值和的差值 https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/⭐⭐⭐⭐⭐
https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/

参考资料:https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/
思路:
显然价值和最小的路径就是只有一个节点的路径。
那么开销实际上就是——一条路径,去掉一个端点。
class Solution {
List<Integer>[] g;
int[] price;
long ans;
public long maxOutput(int n, int[][] edges, int[] price) {
this.price = price;
this.g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList());
for (int[] edge: edges) {
int x = edge[0], y = edge[1];
g[x].add(y);
g[y].add(x);
}
dfs(0, -1);
return ans;
}
// 返回带叶子的最大路径和,不带叶子的最大路径和(分别表示当前节点的两边链)
public long[] dfs(int x, int father) {
long p = price[x];
long maxS1 = p, maxS2 = 0; // maxS1表示完整的,maxS2表示不完整的
for (int y: g[x]) {
if (y != father) {
long[] res = dfs(y, x);
long s1 = res[0], s2 = res[1];
// 更新答案 一条完整的+一条不完整的
ans = Math.max(ans, Math.max(maxS1 + s2, maxS2 + s1));
// 更新路上叶子都选上的最大路径和
maxS1 = Math.max(maxS1, s1 + p);
// 更新路上叶子有一个没被选上的最大路径和(这个没被选上的不是当前节点而是之前枚举过的节点,因为s2中表示有节点没被选)
maxS2 = Math.max(maxS2, s2 + p);
}
}
return new long[]{maxS1, maxS2};
}
}
这道题目的 dfs 过程还没太弄明白。。。
先把 dfs 当模板背过!