随机森林算法介绍及多分类预测的R实现

随机森林（Random Forest）是一种经典的机器学习算法，是数据科学家中最受欢迎和常用的算法之一，最早由Leo Breiman和Adele Cutler于2001年提出。它是基于集成学习（Ensemble Learning）的一种方法，通过组合多个决策树来进行预测和分类，在回归问题中则取平均值。其最重要的特点之一是能够处理包含连续变量和分类变量的数据集。在本文中，我们将详细了解随机森林的工作原理，介绍其在R中的实现及其优缺点。

1. 算法基本原理

1）随机抽样：在随机森林中，每个决策树的训练样本都是通过随机抽样得到的。随机抽样是指从原始训练集中有放回地抽取一部分样本，构成一个新的训练集。这样做的目的是使得每个决策树的训练样本略有差异，增加决策树之间的多样性。

2）随机特征选择：在每个决策树的节点上，随机森林算法会从所有特征中随机选择一部分特征进行分割。这样做的目的是增加每个决策树之间的差异性，防止某些特征过于主导整个随机森林的决策过程。

3）决策树构建：使用随机采样的数据和随机选择的特征，构建多个决策树。决策树的构建过程中，采用通常的决策树算法（如ID3、CART等）。

4）随机森林的预测：当新的样本输入到随机森林中时，它会经过每个决策树的预测过程，最后根据决策集成的方式得到最终的预测结果。对于分类问题，最常见的集成方式是采用多数投票，即根据每个决策树的分类结果进行投票，选择获得最多票数的类别作为最终的预测结果。对于回归问题，可以采用平均预测的方式，即将每个决策树的预测值取平均作为最终的预测结果。n

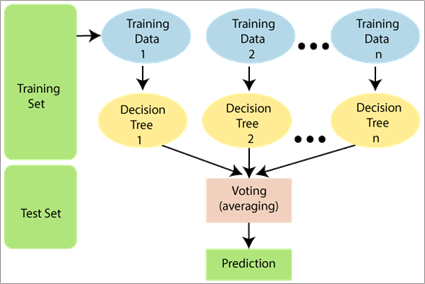
通过随机抽样和随机特征选择，随机森林算法能够减少过拟合风险，提高模型的泛化能力。同时，通过集成多个决策树的预测结果，随机森林能够获得更稳定和准确的预测。

2. 随机森林算法的R实现

以鸢尾花数据集为例，加载需要的包及数据集，未安装的需要先安装。

library(randomForest)
library(datasets)
library(caret)

data<-iris
str(data)

数据集包含150个观测值和5个变量。物种被视为响应变量，为因子变量。

data$Species <- as.factor(data$Species)
table(data$Species)

可以看到结局变量各个分类分布平衡。

1）首先进行随机抽样。

set.seed(222)
ind <- sample(2, nrow(data), replace = TRUE, prob = c(0.7, 0.3))
train <- data[ind==1,]
test <- data[ind==2,]

其中测试集中有106个sample，训练集中有44个sample。

2）然后进行模型构建，这里使用默认参数拟合随机森林模型。

rf <- randomForest(Species~., data=train, proximity=TRUE)

3）参数调整

参数调整是优化随机森林模型性能的重要步骤。下面是一些常用的参数调整方法：

树的数量（ntree）：增加树的数量可以提高模型的稳定性和准确性，但也会增加计算时间。一般来说，增加树的数量直到模型性能趋于稳定为止。

特征数（mtry）：mtry参数控制每个决策树在分裂节点时随机选择的特征数。较小的mtry值会增加树之间的差异性，但可能会降低模型的准确性。较大的mtry值会增加模型的稳定性，但可能会导致模型过度拟合。一般推荐使用默认值sqrt(p)，其中p是特征的总数。

决策树的最大深度（max_depth）：限制决策树的最大深度可以防止过度拟合。通过限制最大深度，可以控制模型的复杂度并提高泛化能力。

节点分割的最小样本数（min_samples_split）：限制节点分割所需的最小样本数可以控制决策树的生长。较小的值会增加模型的复杂性，可能导致过度拟合。较大的值会限制模型的生长，可能导致欠拟合。选择合适的值需要根据数据集的大小和特征的分布进行调整。

节点分割的最小准则（criterion）：决定节点分割的准则，常用的有基尼系数（gini）和信息增益（entropy）。这两个准则在大多数情况下表现相似，通常选择默认值基尼系数。

其他参数：还有其他一些参数可以调整，如样本权重、叶节点最小样本数等，根据具体问题进行调整。

# 如果需要调整参数，可以使用tuneRF()函数进行自动调参。

tuned_rf_model <- tuneRF(train[, -5], train[, 5], ntreeTry = 500,

                       stepFactor = 1.5, improve = 0.01, trace = TRUE,

                       plot = TRUE)

可以看到mtry=3时，OOBerror最小，因此模型中应该设置mtry=3。

在进行参数调整时，可以使用交叉验证来评估模型性能，并选择表现最好的参数组合。例如，可以使用k折交叉验证，将训练集分成k个子集，每次使用其中k-1个子集作为训练数据，剩余一个子集作为验证数据，重复进行k次并计算平均性能指标。

R中的caret包为调整机器学习算法的参数提供了一个很好的工具。但并非所有的机器学习算法都可以在caret中进行调整。只有那些影响较大的算法参数才可以在caret中进行调整。因此，caret中只有mtry参数可供调谐。原因是它对最终准确度的影响，而且它必须根据经验为一个数据集找到。ntree参数则不同，它可以随心所欲地放大，并在一定程度上继续提高精度。它的调整不那么困难或关键，而且可能更多的是受到可用计算时间的限制。

R中实现方式如下：

# 定义参数网格
rf_grid <- expand.grid(mtry = seq(2, 6, by = 1))

# 设置交叉验证方案
control <- trainControl(method = "cv", number = 10)

# 运行交叉验证
rf_model <- train(Species ~ ., data = train, method = "rf", trControl = control, tuneGrid = rf_grid, importance = TURE

# 输出最佳参数组合和性能指标
print(rf_model$bestTune)

print(rf_model$results)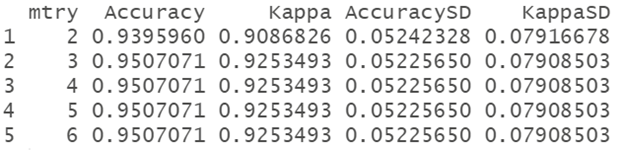

可以看到在mtry=3时，Accuracy最高。

best_model <- rf_model$finalModel

将调优后的参数赋值给best_model。

在上面的代码中，我们首先将数据集划分为训练集和测试集。然后定义了一个包含参数范围（mtry）的网格。接下来，使用trainControl()函数设置了一个十折折交叉验证方案，并运行train()函数来进行模型拟合和性能评估。最后，输出了最佳参数组合和各个参数组合下的性能指标。需要注意的是，在实际应用中，可能需要尝试多个不同的参数网格，并对每个网格进行交叉验证以选择最优参数组合。

3）接下来在测试集中进行预测。

# 预测测试集数据
predictions <- predict(best_model, newdata = test)

# 绘制混淆矩阵
result_matrix<-confusionMatrix(table(predictions, test$Species))
result_matrix

混淆矩阵中显示了预测各个类别的敏感性，特异性等指标，总体Accuracy为0.9388，具有很好的预测效能。

#模型的各个类别预测效能

result_matrix$byClass

#预测各个类别概率

rf_pred <- predict(best_model, test, type = 'prob')
rf_pred <- data.frame(rf_pred)
colnames(rf_pred) <- paste0(colnames(rf_pred), "_pred_RF")

构建绘图数据，该部分在我前面的博客里也讲过做法，详情见http://t.csdn.cn/Z8yGi，这里再呈现一下。

Library(multiROC)
true_label <- dummies::dummy(test_df$Species, sep = ".")
true_label <- data.frame(true_label)
colnames(true_label) <- gsub(".*?\\.", "", colnames(true_label))
colnames(true_label) <- paste(colnames(true_label), "_true")
final_df <- cbind(true_label, rf_pred)
roc_res <- multi_roc(final_df, force_diag=F)
pr_res <- multi_pr(final_df, force_diag=F)
plot_roc_df <- plot_roc_data(roc_res)
plot_pr_df <- plot_pr_data(pr_res)
##AUC值
auc_value<-roc_res_value$AUC
auc_num<-unlist(auc_value)

# 绘制ROC曲线
require(ggplot2)
ggplot(plot_roc_df, aes(x = 1-Specificity, y=Sensitivity)) +
 geom_path(aes(color = Group), size=1.5) +
 geom_segment(aes(x = 0, y = 0, xend = 1, yend = 1),
              colour='grey', linetype = 'dotdash') +
 theme_bw() +
  theme(plot.title = element_text(hjust = 0.5),
       legend.justification=c(1, 0), legend.position=c(.95, .05),
       legend.title=element_blank(),
       legend.background = element_rect(fill=NULL, size=0.5,
                                      linetype="solid", colour ="black"))

评估变量重要性

Importance(best_model)

此处“Mean Decrease Accuracy”和“Mean Decrease Gini”为随机森林模型中的两个重要指标。其中，“mean decrease accuracy”表示随机森林预测准确性的降低程度，该值越大表示该变量的重要性越大；“mean decrease gini”计算每个变量对分类树每个节点上观测值的异质性的影响，从而比较变量的重要性。该值越大表示该变量的重要性越大。

3. 算法优缺点

1）随机森林算法相比于其他机器学习算法具有以下优势：

高准确性：通过组合多个决策树，利用集成学习的方式提高了预测的准确性。它能够处理大量的训练数据，并且对于噪声和缺失数据具有较好的鲁棒性。

可扩展性：可以有效地处理具有大量特征的数据集，并且能够处理高维度的输入。它可以在较短的时间内对大规模数据集进行训练，并且具有较快的预测速度。

特征选择：可以通过计算特征的重要性来评估每个特征对于预测的贡献程度。这可以帮助我们识别出对于问题最为重要的特征，从而进行特征选择和降维，提高模型的效率和性能。

抗过拟合：通过随机选择训练样本和特征的方式，降低了单个决策树过拟合的风险。同时，随机森林中的多个决策树进行投票或平均预测，可以减少模型的方差，提高了泛化能力。

处理非线性关系：能够有效地处理非线性关系，不需要对数据进行过多的预处理或进行特征工程。它可以捕捉到特征之间的复杂非线性关系，从而更好地拟合数据。

鲁棒性：对于缺失值和噪声具有较好的鲁棒性。它可以处理具有缺失值的数据，并且对于噪声和异常值的影响较小。

总的来说，随机森林算法在准确性、可扩展性、特征选择、抗过拟合、处理非线性关系和鲁棒性等方面都具有优势，因此在许多实际应用中被广泛采用。

2）缺点：

决策边界的不连续性：由于随机森林是由多个决策树组成的，因此它的决策边界是由决策树的集合构成的。这可能导致决策边界出现不连续的情况，对于某些问题可能不够精细。

训练时间较长：相比于一些简单的线性模型，随机森林的训练时间可能较长。因为它需要构建多个决策树并进行集成，每个决策树的构建都需要消耗时间。