本篇参考单向循环链表解决约瑟夫问题(C++)整理,先搞懂结构框架,后期根据视频利用c对内容实现,也可以对c有更高的提升。
文章目录
- 1. 链表创建与初始化
- 2. 添加插入、删除和打印函数
- 3. 插入数据并核验
- 4. 解决约瑟夫问题,
- 5. 整体代码及运行结果
- 5.1 代码
- 5.2 运行结果
在大厂面试时,经常会被提出实现约瑟夫问题。那么什么是约瑟夫问题呢?
约瑟夫问题:
n个人围成一个圆圈,分别编号1~n,从第一个人开始顺时针报数为1,报到第m的时候。令其出列,然后再从下一个人重新开始报数,当从1报到m时,报m的人继续出列,以此重复下去,直到所有人都出列为止,获得所有人出列的序号。
当n=8,m=3时,出列的序号如下所示:
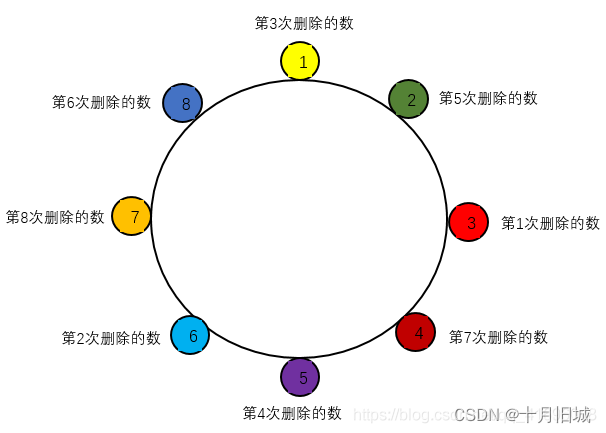
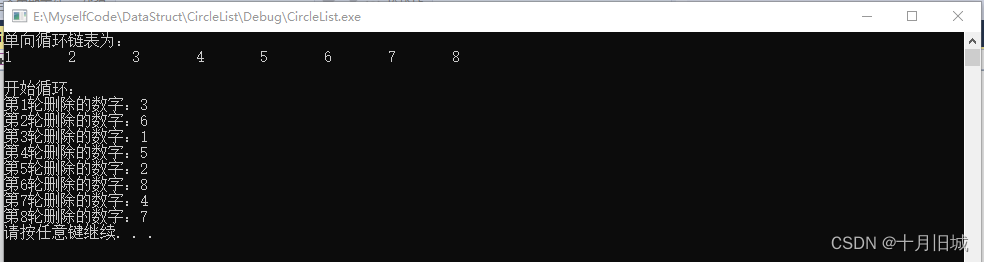
最终删除的序列为:3、6、1、5、2、8、4、7。
C++中有一种数据存储结构与这种首尾相连的环形结构极为相似——单向循环链表。对于单向循环链表的详细介绍可见C++数据结构X篇_06_C++单向循环链表实现。
下面我们将通过单向循环链表去实现约瑟夫问题。
1. 链表创建与初始化
这已经是老生常谈的问题了,在这里就不再赘述了,详情可见笔者之前写的有关链表的博客文章。
//节点定义
class node
{
public:
int data;
node* next;
};
//链表定义
class list
{
public:
int size;
node* head;
};
//链表初始化
list* list_init()
{
list* L=new list;
L->size=0;
L->head=new node;
L->head->data=NULL;
L->head->next=L->head;
return L;
}
2. 添加插入、删除和打印函数
我们创建的链表里面并不含有任何数据,因此我们还需要通过数据插入函数,将数据插入到链表中。由于约瑟夫问题还涉及到数据删除的问题,因此我们还要提供数据删除函数。为了知道我们的数据是否成功插入或删除,我们需要提供打印链表中数据的函数。
//链表插入数据
void list_insert(list *L,int pos,int num)
{
node* new_node=new node;
new_node->data=num;
new_node->next=NULL;
node* pcurrent=L->head;
for (int i = 0; i < pos; i++)
{
pcurrent=pcurrent->next;
}
new_node->next=pcurrent->next;
pcurrent->next=new_node;
L->size++;
}
//删除链表(按值)
void list_delete(list* L,int num)
{
node* pcurrent=L->head->next;
int pos=0;
for (int i = 0; i < L->size; i++)
{
if (pcurrent->data==num)
{
break;
}
pcurrent=pcurrent->next;
pos++;
}
pcurrent=L->head;
for (int i = 0; i < pos; i++)
{
pcurrent=pcurrent->next;
}
pcurrent->next=pcurrent->next->next;
L->size--;
}
//打印链表
void list_print(list *L,int num)
{
node* pcurrent=L->head;
for (int i = 0; i < num; i++)
{
if (pcurrent==L->head)
{
pcurrent=pcurrent->next;
}
cout<<pcurrent->data<<"\t";
pcurrent=pcurrent->next;
}
cout<<endl;
}
这些准备工作都完成之后我们就可以开始正式实现约瑟夫问题了,这里我同样将约瑟夫问题的n设为8、m设为3。
const int n=8;
const int m=3;
3. 插入数据并核验
首先是数据1~8插入链表,同时还可以打印检核一下
//在链表中插入1~8
list* L=list_init();
for (int i = 0; i < n; i++)
{
list_insert(L,i,i+1);
}
cout<<"单向循环链表为:"<<endl;
list_print(L,n);
4. 解决约瑟夫问题,
这明显是一个条件循环问题,只要链表中还有数据它就会一直循环下去。由于报号的过程是从自身开始的,因此除了自身外,还需要往后数两个数即这三个数分别为:pcurrent、pcurrent->next、pcurrent->next->next。当第三个人报号时,把他剔除。并将下次重新报号的人往后移一位,这样就可以与前面循环起来了。
//开始解决约瑟夫问题
cout<<"\n开始循环:"<<endl;
node* pcurrent=L->head;
int iter=1;
while (L->size != 0)
{
for (int i = 0; i < 2; i++)
{
if (pcurrent == L->head) //排除头node
{
pcurrent=pcurrent->next;
}
pcurrent=pcurrent->next;
if (pcurrent == L->head) //排除头node
{
pcurrent=pcurrent->next;
}
}
cout<<"第"<<iter<<"轮删除的数字:"<<pcurrent->data<<endl;
//node* temp_p=pcurrent;
list_delete(L,pcurrent->data);
pcurrent=pcurrent->next;
iter++;
}
至此我们就完成了整个约瑟夫问题。
5. 整体代码及运行结果
5.1 代码
#include <iostream>
using namespace std;
const int n=8;
const int m=3;
//创建单向循环链表
class node
{
public:
int data;
node* next;
};
class list
{
public:
int size;
node* head;
};
list* list_init()
{
list* L=new list;
L->size=0;
L->head=new node;
L->head->data=NULL;
L->head->next=L->head;
return L;
}
//链表插入数据
void list_insert(list *L,int pos,int num)
{
node* new_node=new node;
new_node->data=num;
new_node->next=NULL;
node* pcurrent=L->head;
for (int i = 0; i < pos; i++)
{
pcurrent=pcurrent->next;
}
new_node->next=pcurrent->next;
pcurrent->next=new_node;
L->size++;
}
//删除链表(按值)
void list_delete(list* L,int num)
{
node* pcurrent=L->head->next;
int pos=0;
for (int i = 0; i < L->size; i++)
{
if (pcurrent->data==num)
{
break;
}
pcurrent=pcurrent->next;
pos++;
}
pcurrent=L->head;
for (int i = 0; i < pos; i++)
{
pcurrent=pcurrent->next;
}
pcurrent->next=pcurrent->next->next;
L->size--;
}
//打印链表
void list_print(list *L,int num)
{
node* pcurrent=L->head;
for (int i = 0; i < num; i++)
{
if (pcurrent==L->head)
{
pcurrent=pcurrent->next;
}
cout<<pcurrent->data<<"\t";
pcurrent=pcurrent->next;
}
cout<<endl;
}
int main()
{
//在链表中插入1~8
list* L=list_init();
for (int i = 0; i < n; i++)
{
list_insert(L,i,i+1);
}
cout<<"单向循环链表为:"<<endl;
list_print(L,n);
//开始解决约瑟夫问题
cout<<"\n开始循环:"<<endl;
node* pcurrent=L->head;
int iter=1;
while (L->size != 0)
{
for (int i = 0; i < 2; i++)
{
if (pcurrent == L->head) //排除头node
{
pcurrent=pcurrent->next;
}
pcurrent=pcurrent->next;
if (pcurrent == L->head) //排除头node
{
pcurrent=pcurrent->next;
}
}
cout<<"第"<<iter<<"轮删除的数字:"<<pcurrent->data<<endl;
//node* temp_p=pcurrent;
list_delete(L,pcurrent->data);
pcurrent=pcurrent->next;
iter++;
}
system("pause");
return 0;
}
5.2 运行结果
6. 学习视频地址: 单向循环链表解决约瑟夫问题