• 已排除非本人创作部分

摘要

• 针对问题一，我们首先对所有团队的数据做了正态性检验，共x次作业，每次作业成绩分布均可用正态分布描述。其次，我们对团队之间的成绩变化做了格兰杰因果检验，列出了成绩变化相关的一部分团队，认为这些团队之间存在在互相帮助的现象。

• 针对每一次测试，我们将所有团队的得分标准化处理，通过对每个题目加权相加的方法，得到每个队伍标准化后的平时分总分。再对团队的平时分总分做极差标准化处理，得到平时分总分的约化分数和约化排名。

• 为了解决平时分打分问题，我们选取了极差排名，方差排名，最高分排名，最低分排名，约化分数，约化排名六个指标，使用加权线性回归方法得到最终平时分打分。

• 为了预测团队的期末得分，我们分别使用了灰色模型和时间序列预测模型来预测团队的期末得分。事实上，考虑到该门课程还将继续开设下去，不妨根据本学期得到的（平时，签到）--（期末）得分情况，建立一个智能回归模型，以便预测下一届课程的期末得分情况。对此,我们还将全部团队分成训练组(7/10)与测试组(3/10),利用XGBoost回归得到了一个模拟的结果

• 通过汇总附件一中的签到分数、第二问得到的报告平时分以及第三问预测的期末分，我们预测所有同学的期末总分。我们发现，签到分数，平时分分数，期末分分数，期末总分分数均不满足正态分布。我们随后又建立了基于（总分-平时-期末）对（签到）的随机森林分类模型。模型的效果很好，因此，我们认为学生得分与签到情况有较大关系。

关键词

• 统计模型 预测模型 随机森林

问题重述

问题背景

• 课程x分数由平时分数和期末分数构成，各占比50%。平时分又包含两部分：x次赛题求解思路报告的42分；x次签到的8分。

• 本门课程共评价x次赛题求解思路报告。现在需要将这x次报告分数转换为满分为42分的平时分数。然后，通过对同学们的期末论文进行评价，得到满分为50分的期末分数。

• 我们需要挖掘出团队x次报告分数的规律；分析x次报告分数，提出六个指标打分，从而得到满分为42分的平时分；基于x次报告的分数，预测团队的期末分数，并论证合理性；汇总签到分数、报告平时分以及预测的期末分，预测并统计分析所有同学的期末总分。

问题分析

问题一分析

• 在将存在数据缺失的组的单项成绩进行插值补全后，大致发现，在进行正态数据检验后，基本可以接受各组成绩分布成正态分布。此外，不能排除各组之间存在相互作用的影响，因此，进行格兰杰因果检验，对各组之间成绩变化进行因果检验。

问题二分析

• 考虑成绩打分的公平性，给分应当完全依据学生的成绩，这样一来，我们可以选择的指标并不多，因此选取：极差排名（倒序）0.04，方差排名（倒序）0.04，最高分排名（正序）：0.04，最低分排名（倒序）：0.04，约化分数0.8，约化排名（正序）0.04这六项指标，并赋予权重。对于数学建模实战来说，各个学习模块的重要性并不相同，对九次成绩因涉及不同模块，故提出一种权重矩阵来获取约化成绩。最后对各组各项成绩加权取和后作用最终平时分。

问题三分析

• 考虑到各次小组作业并非单纯按难易程度进行划分的，各次小组作业所设计的数学建模领域不同，如涉及“优化”问题，“评价问题”等，故此评价各组实力变量并不单一。此外，考虑到期末作业的难易未知，涉及领域未知，故须对各次作业消除各变量影响后再进行预测。对于单次作业“难易度”评判，可以简单的从题一中各组分布规律可以定性看出，为了量化这一标准，我们可以对x次的x项数据取均值并除以单次总分从而获得x次作业的难度因子。对于“涉及领域问题”，则对各次题目进行分类。为简化模型，采取“难易度”，“涉及的领域”对各个小组的成绩进行加权和降权处理，从而得到不受题目和小组擅长领域不同影响的x次成绩。再对x组x次成绩采用灰色预测和时间序列模型预测，从而得出能代表绝对实力的各组期末成绩的预测。

基本假设

1. 成绩的取得均是合乎规则的
2. 评估平时成绩时,仅考虑课程作业中给出的数据

符号说明

 

数据预处理

1.数据预处理问题贯穿了我们成绩分析的全过程。事实上，数据列表唯一的缺陷值是几支队伍未参加某几次测试导致的。我们填补这些成绩的基本原则是，这些成绩必须基于他们在其他几次测试中的成绩。这一考量是由课程成绩的专业性，公平性决定的。然而，我们发现，绝对成绩是一个相对不稳定的值。同时，对于数学建模这种专业性强，难度高的题目，我们最应该比较的是相对成绩而不是绝对成绩。而相对成绩的取得应该在同一题目下考量。因此，我们需要对成绩做标准化处理。

 

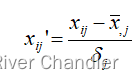
2.缺省值由该队伍全部有效的标准化后的测试得分的均值填充。

3.数据加权：数学建模由多个不同模块组成，不同模块有着不同的作用，在不同的比赛中有着重要性不同的地位。因此，对数学建模模块的加权必不可少。

4.总得分的极化处理：通过极化处理，我们可以在成绩中体现出同学之间的区分度，从而保证得分的公平性。

 

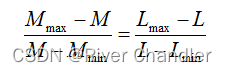
问题一求解

我们对题给数据做基本的处理：

我们分别使用了S-W检验与K-S检验两种方法分析数据的正态性与分布同一性。

S-W检验的步骤如下：

1.提出假设：S-W检验的原假设是数据符合正态分布，备择假设是数据不符合正态分布。这意味着我们希望证明数据来自正态分布，或者尝试找到证据表明数据不符合正态分布。

2.排序数据：将待检验的数据按照从小到大的顺序进行排列。

3.计算期望值和方差：根据样本大小和排序后的样本值，计算出期望值和方差。这些统计量用于计算S-W统计量。

4.计算S-W统计量：利用期望值和方差，计算S-W统计量。S-W统计量的取值范围在0到1之间，越接近1表示数据越接近正态分布。

5.计算临界值：根据样本大小和显著性水平，查找对应的临界值。临界值是用于判断S-W统计量是否显著。

6.比较统计量和临界值：将计算得到的S-W统计量与临界值进行比较。如果S-W统计量小于临界值，则接受原假设，即数据符合正态分布；如果S-W统计量大于临界值，则拒绝原假设，即数据不符合正态分布。

K-S检验的步骤如下：

1.提出假设：K-S检验的原假设是两个样本来自同一分布，备择假设是两个样本来自不同的分布。通过检验来确定两个样本是否有显著的差异。

2.计算经验分布函数（ECDF）：将两个样本的数据合并，并分别计算每个样本的经验分布函数。经验分布函数描述了样本中小于等于某个值的观测频率。

3.计算K-S统计量：通过比较两个样本的经验分布函数的最大差异，计算出K-S统计量。K-S统计量的值代表了两个样本的最大分布差异。

4.计算临界值：根据显著性水平和样本大小，查找对应的临界值。临界值用于判断K-S统计量是否显著。

5.比较统计量和临界值：将计算得到的K-S统计量与临界值进行比较。如果计算得到的K-S统计量小于临界值，则接受原假设，即两个样本来自同一分布；如果K-S统计量大于临界值，则拒绝原假设，即两个样本来自不同的分布。

数据的正态性检验直方图

略

格兰杰因果检验的步骤如下：

1.提出假设：格兰杰因果检验的原假设是某队某次分数(X)不因果影响另一队队同次分数(Y)，备择假设是某队某次分数因果影响另一队队同次分数。通过检验来判断X是否对Y具有因果关系。

2.准备时间序列数据：收集包含某队某次分数和Y的时间序列数据，并确保数据满足平稳性和其他统计性质的要求。

3.拟合时间序列模型：分别对某队某次分数和Y拟合合适的时间序列模型，例如自回归模型（AR）或向量自回归模型（VAR）。

4.进行格兰杰因果检验：对于拟合好的模型，使用统计方法来计算格兰杰因果检验的统计量(F统计量和p值)。

5.判断因果关系：比较计算得到的统计量与预设的显著性水平，通常为0.05或0.01。如果计算得到的统计量小于显著性水平对应的临界值，则接受原假设，即X对Y不存在因果影响；如果统计量大于临界值，则拒绝原假设，即X对Y存在因果影响。

格兰杰因果检验的优点在于它能够提供因果关系的定量度量，对时间序列数据中的因果性问题提供了一种统计框架。对所有队伍的成绩变化做分析。通过格兰杰因果检验，找出成绩变化相关的队伍。

格兰杰因果检验表

略

也就是说，我们有理由相信这些小组在完成作业时存在互相帮助的现象。

问题二求解

        我们考虑成绩打分的公平性，也就是说，我们的给分应当完全依据学生的成绩，这样一来，我们可以选择的指标并不多：

        提出六个指标并进行打分，从而得到满分为42分的平时分；极差排名（倒序）0.04，方差排名（倒序）0.04，最高分排名（正序）：0.04，最低分排名（倒序）：0.04，约化分数0.8，约化排名（正序）0.04。同样的，这些成绩也通过极化处理得出。

        对于数学建模实战来说，各个学习模块的重要性并不相同，我们选取了一种权重矩阵

权重矩阵略

依据我们在数据预处理中提到的方法，可以计算出各个队伍的成绩

问题三求解

        我们在该题中是要预测x个团队的期末分数，我们可以采用灰色预测和时间序列模型预测

灰色预测模型

分析步骤

        在建立灰色预测模型GM(1,1)前，需要对时间序列进行级比检验。若通过级比检验，则说明该序列适合构建灰色模型，若不通过级比检验，则对序列进行“平移转换”，从而使得新序列满足级比值检验。

        灰色预测模型要经过检验才能判定其是否合理，只有通过检验的模型才能用来作预测，系统主要通过后验差比C值来对灰色预测模型进行检验。

级比检验结果表

        略

灰色模型构建

        发展系数

        灰色作用量

        后验差比C值

模型拟合结果表

        略

时间序列预测ARIMA模型（以13队为例）

        ARIMA模型是一种基于时间序列的统计模型，用于预测未来的趋势和规律。

        自回归（AR）部分：表示当前获得的分数与过去若干个获得的分数之间的关系，即当前值的预测值是过去若干个值的线性组合。AR部分的阶数为p，表示使用过去p个获得的分数来预测当前获得的分数。

        差分（I）部分：表示对时间序列进行差分处理，以消除序列中的趋势和季节性等影响，使其变得平稳。I部分的阶数为d，表示对时间序列进行d次差分处理。

        移动平均（MA）部分：表示当前获得的分数与过去若干个时刻的误差（即实际值与预测值之差）之间的关系，即当前值的预测值是过去若干个误差的线性组合。MA部分的阶数为q，表示使用过去q个误差来预测当前获得的分数。

        ARIMA模型可以通过对时间序列的历史数据进行拟合，得到模型的参数，从而进行未来值的预测。在实际应用中，ARIMA模型通常需要进行参数调整和模型优化，以提高预测的准确性和可靠性。

        良好的ARIMA模型需要满足两个条件：

1.ARIMA模型要求序列满足平稳性，查看ADF检验结果，根据分析t值，分析其是否可以显著性地拒绝序列不平稳的假设(P<0.05)。

2.ARIMA模型要求模型具备纯随机性。根据Q统计量的P值(P>0.05)对模型白噪声进行检验，也可以结合信息准则AIC和BIC值进行分析（越低越好），也可以通过模型残差ACF/PACF图进行分析根据模型参数表，得出模型公式结合时间序列分析图进行综合分析，得到向后预测的阶数结果。

ADF检验表

        略

XGboost模型

        XGBoost是一种基于决策树的集成学习方法，可以用于分类和回归问题。我们正需要解决的问题就是对平时成绩取回归。

        我们构建的XGBoost模型包括：

1.决策树：XGBoost使用多个决策树进行集成学习，每个决策树都是一种弱学习器，通过多个弱学习器的集成来提高整体预测的准确性和鲁棒性。

2.优化目标函数：XGBoost使用梯度提升（Gradient Boosting）目标函数，通过不断迭代优化目标函数，来提高模型的预测能力和泛化能力。

3.正则化函数：XGBoost使用正则化技术，包括L1正则化和L2正则化，来控制模型的复杂度，避免过拟合。

        考虑到该门课程还将继续开设下去，不妨根据本学期得到的（平时，签到）--（期末）得分情况，建立一个智能回归模型，以便预测下一届课程的期末得分情况。这样，只需要输入相关平时，签到分，即可得到最终的期末分数。这将极大得提高评分效率。

XGBoost回归模型的分析步骤如下：

1. 通过训练集数据来建立XGBoost回归模型。

2. 通过建立的XGBoost来计算特征重要性。

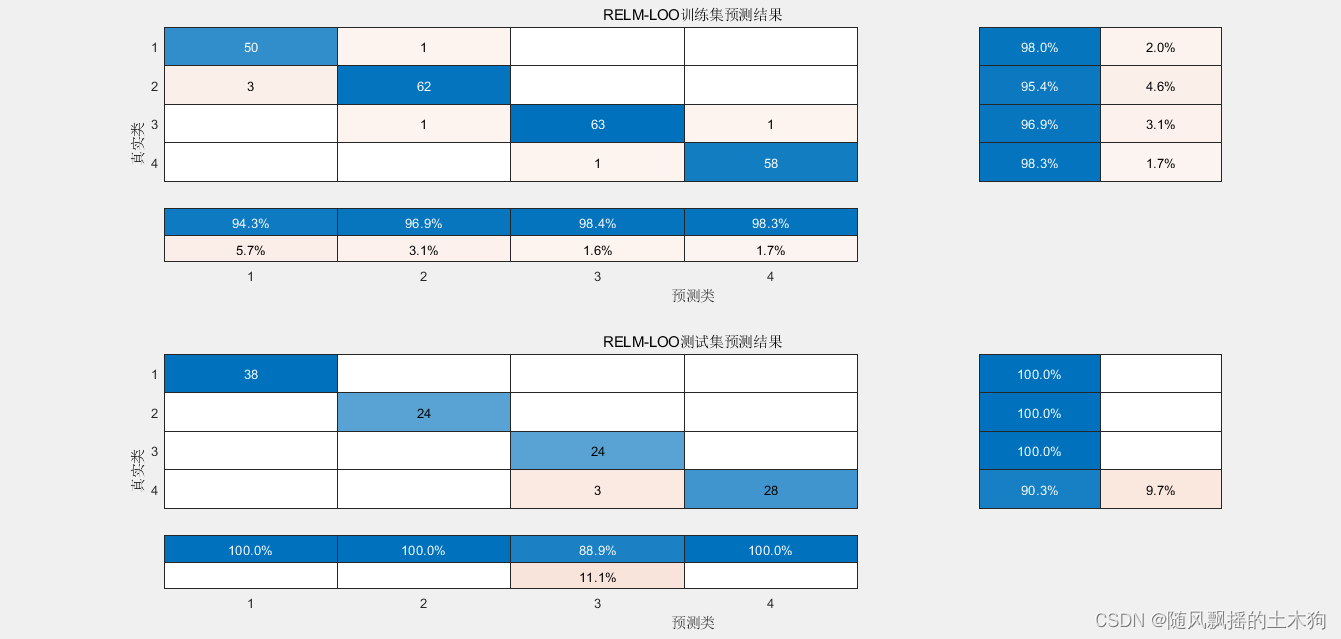
3. 将建立的XGBoost回归模型应用到训练、测试数据，得到模型评估结果。

4. 对模型进行评价。