cf 比赛 03

news2024/11/14 3:00:27

2021.04.28

训练地址

B. Bananas in a Microwave

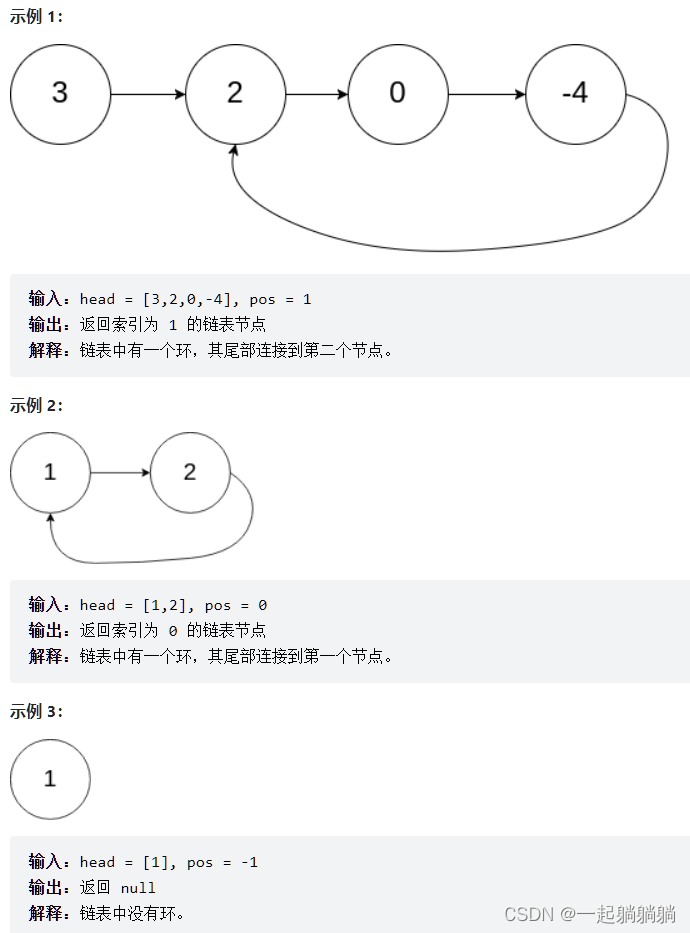
  • 题意：一开始的时候手里的数是0
    在这里插入图片描述
  • 这个题一开始想复杂了. 其实很简单. 我们想一个性质，我们用背包dp做这个题，从大到小枚举体积 j. 然后状态转移是从前往后推（不是之前的那个找前驱状态）.那么，我们对体积做变换（就是两个操作）。如果所得的体积之前已经出现过，就 break。这样子并不会影响。因为如果 v 1 → v 2 → v 3 v_1 \rightarrow v_2 \rightarrow v_3 v1​→v2​→v3​，如果从 v 1 v_1 v1​ 到 v 2 v_2 v2​ 的时候，发现 v 2 v_2 v2​ 已经搜索过（但是不是当前种类的操作转移的），那么 v 3 v_3 v3​ 仍然可以被更新答案。因为在搜索 v 2 v_2 v2​ 的时候， v 3 v_3 v3​ 的状态就可以搜索到.
#include<bits/stdc++.h>
using namespace std;
const int N = 210, M = 100010;
typedef long long ll;
int f[M];
int main()
{
    memset(f, -1, sizeof f);
    int n, m;
    scanf("%d%d", &n, &m);
    f[0] = 0;
    for(int i = 1; i <= n; i++){
        ll op, x, y;
        scanf("%lld%lld%lld", &op, &x, &y);
        for(ll j = m; j >= 0; j--){
            if(f[j] == -1) continue;
            ll z = j;
            for(ll k = 1; k <= y; k++){
                if(op == 1) z = (z * 100000 + x + 100000 - 1) / 100000;
                else z = (z * x + 100000 - 1) / 100000;
                if(z > m) break;
                if(f[z] != -1) break;
                f[z] = i;
            }

        }
    }
    for(int i = 1; i <= m; i++){
        printf("%d%c", f[i], i == m ? '\n' : ' ');
    }
    return 0;
}

C. Two Houses

  • 将此题改编一下：有一张竞赛图，告诉每个点的入度，问是否存在两个点 A A A 和 B B B，使得 A A A 可以到 B 且 B 可以到 A. 并且使得 ∣ d i n [ A ] − d i n [ B ] ∣ |din[A] - din[B]| ∣din[A]−din[B]∣ 最大。
  • 我们按照入度从小到大排序，那么强连通分量的块一定是依次排列的。这个可以画画图，用反证法证明。
  • 我们这样找块与块之间的分界线：假设枚举到第 i i i 个起点，如果 i i i 和 i + 1 i+1 i+1 之间的分界线上的边全是指向右边的，那么这个分界线就是两个强连通块的分界线。而这个等价于：前 i 个点的出度之和 - 前 i 个点内部的出度之和 i ∗ ( i − 1 ) / 2 i * (i - 1) / 2 i∗(i−1)/2 = 分界线上的边的数量 i ∗ ( n − i ) i * (n - i) i∗(n−i)
  • 有一个地方需要注意，就是答案无解的时候，不等价于 ans = 0. 因为可以某个点的数量不少于两个的强连通分量中的入度都是一样的。
  • 因此判断那个地方要加上 i ! = l a s t i != last i!=last.
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef long long ll;
const int N = 510;
typedef pair<ll, ll> P;
P din[N];
int main()
{
    ll n;
    scanf("%lld", &n);
    for(int i = 1; i <= n; i++){
        scanf("%lld", &din[i].x);
        din[i].y = i;
    }
    sort(din + 1, din + n + 1);
    ll sum = 0, sum2 = 0;
    int last = 1, A, B;
    ll ans = -1;
    for(ll i = 1; i <= n; i++){
        sum += n - din[i].x - 1;
        sum2 += din[i].x;
        if(sum == (i - 1) * i / 2 + i * (n - i)){
            if(i != last && ans < din[i].x - din[last].x){
                A = din[last].y, B = din[i].y;
                ans = din[i].x - din[last].x;
            }
            last = i + 1;
        }
    }
    if(ans == -1){
        printf("! 0 0\n");
    }
    else{
        printf("! %d %d\n", A, B);
    }
    return 0;
}

D. Christmas Game

在这里插入图片描述

  • 对于确定的根节点，记 d ′ = d e p t h / k d' = depth / k d′=depth/k。只有d’是奇数的时候才会有用。因为如果一个人把若干硬币从偶数点转移到了奇数点，那么这个人可以做重复的操作，把相同数量的硬币再移动到偶数点。那么，这就像一个Nim台阶游戏，只不过由若干相互独立的台阶组成。因此我们对每一个台阶，奇数位置的数字异或起来，然后把所有台阶再异或起来，如果不为0，先手赢，如果为0，先手输.
  • 那么，我们可以跑一个树形dp，记录下来每个点离根节点距离为 d m o d    2 k d \mod 2k dmod2k 的点权异或和，存在 d p ( u , k ) dp(u,k) dp(u,k)里面. 先跑一遍dfs记录下来以当前节点为子树的dp数组，然后再跑一遍树形dp，计算出父结点的最终答案后，把子节点所在子树扣掉，然后父结点剩余子树对子结点答案的贡献，计算答案。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010, K = 50, M = 200010;
vector<int> a(N), win(N);
int dp[N][K];
int n, k2, k;
int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u, int fa)
{
    dp[u][0] = a[u];
    for(int i = h[u]; i != -1; i = ne[i]){
        int v = e[i];
        if(v == fa) continue;
        dfs(v, u);
        for(int i = 1; i < k2; i++) dp[u][i] ^= dp[v][i - 1];
        dp[u][0] ^= dp[v][k2 - 1];
    }
}
void dfs2(int u, int fa, vector<int>& my_xor)
{
    vector<int> final_xor(K);

    //my_xor 是从父结点传递过来，是除去当前u所在子树，fa以及其它子树的结果.
    for(int i = 1; i < k2; i++){
        final_xor[i] = my_xor[i - 1] ^ dp[u][i];
    }
    final_xor[0] = my_xor[k2 - 1] ^ dp[u][0];


    int res = 0;

    //注意这里是从k开始，千万别弄错. 因为我们只需要计算 depth / k 为奇数的情况

    for(int i = k; i < k2; i++) res ^= final_xor[i];
    win[u] = (res != 0);

    for(int i = h[u]; i != -1; i = ne[i]){
        int v = e[i];
        if(v == fa) continue;
        auto xor_send = final_xor;

        //把当前u的最终结果除去以v为根节点的子树
        for(int i = 1; i < k2; i++){
            xor_send[i] ^= dp[v][i - 1];
        }
        xor_send[0] ^= dp[v][k2 - 1];

        dfs2(v, u, xor_send);
    }
}
int main()
{
    scanf("%d%d", &n, &k);
    k2 = 2 * k;
    memset(h, -1, sizeof h);
    for(int i = 1; i < n; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    dfs(1, -1);
    vector<int> tmp(K);
    for(int i = 0; i < K; i++) tmp[i] = 0;
    dfs2(1, -1, tmp);
    for(int i = 1; i <= n; i++){
        printf("%d%c", win[i] ? 1 : 0, i == n ? '\n' : ' ');
    }
    return 0;
}

F. Playlist

  • 题意：
    在这里插入图片描述
  • 其实这个题，一开始想的是需要模拟出来这个过程（其实这个题和 2020 ec-final 的热身赛第一题的题意有点像），但是我们会发现，有一个很麻烦的问题，就是如果直接用链表模拟这个过程，可能会超时。
  • 但是，我们发现一个性质，我们在循环枚举的时候，只有每次当这个数紧跟的数字被删掉的时候，才会对后续的数字有影响。那么，我们可以用一个队列来维护有那些数字的后面紧跟的数字被删掉了。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N], ne[N];
bool st[N];
int main()
{
    int T;
    scanf("%d", &T);
    while(T--){
        int n;
        scanf("%d", &n);
        fill(st, st + n + 1, 0);
        queue<int> que;
        vector<int> ans;
        for(int i = 1; i <= n; i++){
            scanf("%d", &a[i]);
            ne[i] = i + 1;
            que.push(i);
        }
        ne[n] = 1;
        while(que.size()){
            int id = que.front(); que.pop();
            int nxt = ne[id];
            if(!st[id] && __gcd(a[id], a[nxt]) == 1){
                ans.push_back(nxt);
                st[nxt] = true;
                ne[id] = ne[nxt];
                que.push(id);
            }
        }
        printf("%d ", (int)ans.size());
        for(auto p : ans){
            printf("%d ", p);
        }
        printf("\n");
    }
    return 0;
}

G. Skyline Photo

  • 题意：
    在这里插入图片描述
  • 首先思考这个，我们定义 d p [ i ] dp[i] dp[i] 为从 1 1 1 ~ i i i 的区间集合的最优方案的值。那么，我们可以从 1 1 1 ~ i − 1 i - 1 i−1 枚举最右边的划分边界是什么，即分成 i i i ~ j − 1 j - 1 j−1即 d p j − 1 dp_{j-1} dpj−1​ ，以及从 j j j 到 i i i 作为一个区间的方案。
  • 实际上，我们可以发现，当我们枚举到 i i i 的时候，我们只需要找到左边第一个比 h i h_i hi​ 小的元素 h j h_j hj​，把 i i i 加到和 j j j 同一个区间里面去，更新答案， d p i = d p j j dp_i = dp_jj dpi​=dpj​j。那么我们就是枚举从 j j j又到 i i i 左侧的分界线，而这之间的元素一定是大于 h i h_i hi​，即 d p i = max ⁡ { d p k − 1 + b i , d p i } dp_i = \max\{dp_{k-1}+b_i, dp_i\} dpi​=max{dpk−1​+bi​,dpi​}， j + 1 ≤ k ≤ i j + 1 \le k \le i j+1≤k≤i. 这可以用一个线段树维护最大值.
  • 因为我们之前计算的 d p j dp_j dpj​ 已经是 1... j 1 ... j 1...j 的最优解。因此可以这样做。
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 300010;
struct node
{
    int l, r;
    ll maxv;
}tr[N * 4];
int n;
ll dp[N], h[N], b[N], stk[N];
void pushup(int u)
{
    tr[u].maxv = max(tr[2 * u].maxv, tr[2 * u + 1].maxv);
}
void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if(l == r) {
        tr[u].maxv = -1e18;
        return;
    }
    int mid = (l + r) / 2;
    build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);
    pushup(u);
}
void modify(int u, int x, ll v)
{
    if(tr[u].l == x && tr[u].r == x) {
        tr[u].maxv = v;
    }
    else{
        int mid = (tr[u].l + tr[u].r) / 2;
        if(x <= mid) modify(2 * u, x, v);
        else modify(2 * u + 1, x, v);
        pushup(u);
    }
}
ll query(int u, int l, int r)
{
    if(l <= tr[u].l && tr[u].r <= r){
        return tr[u].maxv;
    }
    int mid = (tr[u].l + tr[u].r) / 2;
    ll v = -1e18;
    if(l <= mid) v = max(v, query(2 * u, l, r));
    if(r > mid) v = max(v, query(2 * u + 1, l, r));
    return v;
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%lld", &h[i]);
    }
    for(int i = 1; i <= n; i++){
        scanf("%lld", &b[i]);
    }
    build(1, 1, n);
    int tt = 0;
    for(int i = 1; i <= n; i++){
        while(tt && h[stk[tt]] >= h[i]) tt--;
        int j = stk[tt];
        //这个地方一定要写成数组下标，不要写成数组元素！
        stk[++tt] = i;
        if(j){
            dp[i] = dp[j];
            ll v = query(1, j, i - 1);
            dp[i] = max(dp[i], v + b[i]);
        }
        else{
            dp[i] = b[i];
            if(i != 1){
                ll v = query(1, 1, i - 1);
                dp[i] = max(dp[i], v + b[i]);
            }
        }
        modify(1, i, dp[i]);
    }
    printf("%lld\n", dp[n]);
    return 0;
}

H. Useful Edges

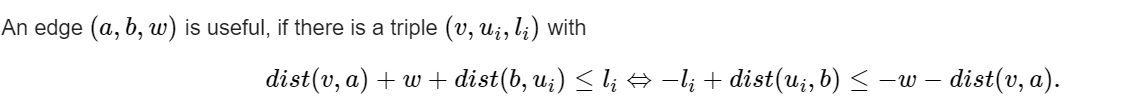
在这里插入图片描述

  • 思路：
    在这里插入图片描述
    我们固定了起点u，有很多终点 v，那么对于每一条边 (a, b)，想知道 b 离最近的终点 v 的距离. 那么可以转化为多源最短路问题，起点就是所有的 v，跑一遍 dijkstra，建立一个超级源点 S，然后向每一个终点 v 连边，边权是 − l i -l_i −li​. 因为 dijkstra 不能有负权边，那么把每个边加上一个很大的数字就可以了.
#include<bits/stdc++.h>
using namespace std;
const int N = 610;
typedef long long ll;
const ll INF = 0x3f3f3f3f3f3f3f3fLL;
ll dist[N][N], g[N][N], qs[N][N], d[N];
bool ok[N][N], st[N];
int n, m;
void dijkstra(int u)
{
    memset(d, 0x3f, sizeof d);
    memset(st, false, sizeof st);
    ll tmp = 1e9;
    for(int j = 1; j <= n; j++){
        if(qs[u][j]) d[j] = tmp - qs[u][j];
    }
    for(int i = 1; i <= n; i++){
        int t = -1;
        for(int j = 1; j <= n; j++){
            if(!st[j] && (t == -1 || d[t] > d[j])) t = j;
        }
        st[t] = true;
        for(int j = 1; j <= n; j++){
            d[j] = min(d[j], d[t] + g[t][j]);
        }
    }
    for(int i = 1; i <= n; i++) if(d[i] != INF) d[i] -= tmp;
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(g, 0x3f, sizeof g);
    memset(dist, 0x3f, sizeof dist);
    
    //这个地方一定把自环初始化为0. 原因在于如果后面的qs中的u可能和某条边的端点重合
    //如果不初始化为0的话，那么 dist[i][i] 就不为0，就会使得答案变小. 
    for(int i = 1; i <= n; i++) g[i][i] = dist[i][i] = 0;
    for(int i = 0; i < m; i++){
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[a][b] = g[b][a] = w;
        dist[a][b] = dist[b][a] = w;
    }
    for(int k = 1; k <= n; k++){
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
            }
        }
    }


    int q;
    scanf("%d", &q);
    while(q--){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        qs[a][b] = qs[b][a] = c;
    }
    for(int u = 1; u <= n; u++){
        dijkstra(u);
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                if(dist[u][i] == INF || g[i][j] == INF || d[j] == INF) continue;
                ok[i][j] |= (dist[u][i] + g[i][j] + d[j] <= 0);
            }
        }
    }
    int ans = 0;
    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++){
            ans += ok[i][j];
        }
    }
    printf("%d\n", ans);
}
  • 当然这个题还可以这么想，原图中所有边都变成之前的相反数，现在加入一条边 ( u , v , l ) (u, v, l) (u,v,l)，问是否存在一条经过 ( u , v ) (u, v) (u,v) 的环，并且路径长度为非负的. 这样子的话，环上的每条边都是合法的，并且每条边两个端点在新图上的距离都是不小于 g ( i , j ) g(i,j) g(i,j) 的。
  • 因此我们就转化为求最长路的问题。
  • 回忆 Floyd 的原理，第一层的 k 是枚举中转节点，并且 Floyd 求的是简单路径的最短路。因此，我们在求得时候，让 qs[i][j] = qs[j][i] = min(qs[i][j], qs[i][k] - dist[k][j])，那么就限制了中转节点，这样子就使得环只走一条正边，即不会走两条类似于 ( u , v , l ) (u, v, l) (u,v,l) 一样的边.
#include<bits/stdc++.h>
using namespace std;
const int N = 610;
typedef long long ll;
const ll INF = 0x3f3f3f3f3f3f3f3fLL;
ll dist[N][N], g[N][N], qs[N][N], d[N];
int n, m;
int main()
{
    scanf("%d%d", &n, &m);
    memset(g, 0x3f, sizeof g);
    memset(dist, 0x3f, sizeof dist);

    //这个地方一定把自环初始化为0. 原因在于如果后面的qs中的u可能和某条边的端点重合
    //如果不初始化为0的话，那么 dist[i][i] 就不为0，就会使得答案变小.
    for(int i = 1; i <= n; i++) g[i][i] = dist[i][i] = 0;
    for(int i = 0; i < m; i++){
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[a][b] = g[b][a] = w;
        dist[a][b] = dist[b][a] = w;
    }
    for(int k = 1; k <= n; k++){
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
            }
        }
    }


    int q;
    scanf("%d", &q);
    while(q--){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        qs[a][b] = qs[b][a] = c;
    }

    for(int k = 1; k <= n; k++){
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                qs[i][j] = qs[j][i] = max(qs[i][j], qs[i][k] - dist[k][j]);
            }
        }
    }
    int ans = 0;
    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++){
            ans += (qs[i][j] >= g[i][j]);
        }
    }
    printf("%d\n", ans);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/713535.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

记录 windows11 qemu安装 麒麟操作系统的经历

记录 windows11 qemu安装 麒麟操作系统的经历

因为本人供职的公司&#xff0c;要求国产化环境很多的软件&#xff0c;同时为了方便docker部署&#xff0c; 所以开启了 qemu虚拟aarch64环境的经历&#xff0c;用的软件如下&#xff1a; 有需要的私信&#xff0c;存在了&#xff0c;阿里云盘&#xff0c;百度云盘没有会员就是…
阅读更多...
大厂面试测试岗，你一个很小的错误就能让你被淘汰

大厂面试测试岗，你一个很小的错误就能让你被淘汰

背景介绍 前后参加过几家互联网公司的测试开发岗位面试&#xff0c;其中两次百度的面试&#xff0c;一次止步三面&#xff0c;另一次止步于四面。这里就主要总结一下百度的面试经历和心得体会。总体感觉百度的面试官比较注重基础&#xff0c;问题不难但是覆盖范围比较全面。相…
阅读更多...
栈，栈帧Stack Frames和函数调用过程Control Flow

栈，栈帧Stack Frames和函数调用过程Control Flow

栈其实就是计算机系统内存中的一小块。栈是一块特殊的内存区域&#xff0c;栈在内存中的增长方向是向低地址扩展&#xff0c;%rsp寄存器存储栈的最低地址&#xff0c;即栈顶元素的地址。这种栈结构在程序中的应用有助于实现函数调用、局部变量的管理以及递归等功能。 Push和Pop…
阅读更多...
Blazor 自定义可重用基础组件之 CheckBox

Blazor 自定义可重用基础组件之 CheckBox

Blazor 原生提供的基础组件实在是一言难尽&#xff0c;这给许多Blazor UI公司很多机会。可是试用了不少如AntDisgen、BootstrapBlazor等&#xff0c;总会有一些难尽如意的地方。还是自己做丰衣足食吧。 首先是带Label的CheckBox&#xff0c;代码如下&#xff1a; <p><…
阅读更多...
HTML5开发工程师岗位的职责说明文（合集）

HTML5开发工程师岗位的职责说明文（合集）

HTML5开发工程师岗位的职责说明文1 职责&#xff1a; 1、根据产品设计文档和视觉文件&#xff0c;利用HTML5&#xff0c;Javascript相关技术实现web端的界面效果、交互和功能; 2、基于HTML5.0的标准进行页面制作&#xff0c;编写可复用的用户界面组件; 3、负责分析和解决前端…
阅读更多...
30多个小程序一键发布——miniprogram-ci

30多个小程序一键发布——miniprogram-ci

概述 miniprogram-ci 是从微信开发者工具中抽离的关于小程序/小游戏项目代码的编译模块。 开发者可不打开小程序开发者工具&#xff0c;独立使用 miniprogram-ci 进行小程序代码的上传、预览等操作。 miniprogram-ci 从 1.0.28 开始支持第三方平台开发的上传和预览&#xff0…
阅读更多...
[DBT-05509] Failed to connect to the specified database (orcl).

[DBT-05509] Failed to connect to the specified database (orcl).

同事在arm上测试19c部署时&#xff0c;发截图给我说dbca建库有告警&#xff0c;无法进行&#xff0c; Cause- OS Authentication might be disabled for this database (orcl). Action Specify a valid sysdba user name and password to connect to the database. 查找到的…
阅读更多...
Windows安装ciphey编码工具，编码工具战神，cry简单题绝对克星！

Windows安装ciphey编码工具，编码工具战神，cry简单题绝对克星！

TA是什么 一款智能化的编码分析解码工具&#xff0c;对于CTF中复杂性编码类题目可以快速攻破。 编码自动分析解码的神器。 如何安装 Windows环境 Python 3.8 64位&#xff08;最新的版本不兼容&#xff0c;32位的也不行&#xff09; 方便起见&#xff0c;我直接给一个3.8.…
阅读更多...
【花雕】全国青少年机器人技术一级考试备考实操搭建手册2

【花雕】全国青少年机器人技术一级考试备考实操搭建手册2

目录 1、秋千 2、跷跷板 3、搅拌器 4、奇怪的钟 5、起重机 6、烤肉架 7、手摇风扇 8、履带车 9、直升机 10、后轮驱动车 游乐场里的跷跷板 跷跷板&#xff08;又作翘翘板&#xff09;&#xff0c;又称为摇摇板&#xff0c;是指以某些东西作为支点&#xff0c;支撑著很长但十分…
阅读更多...
MongoDB 获取数组中匹配到的第一个元素对象

MongoDB 获取数组中匹配到的第一个元素对象

例如当前test库中的grade集合中有两条文档数据，如下图所示： 相关的两个实体映射类如下： import lombok.Data; import org.springframework.data.annotation.Id; import org.springframework.data.mongodb.core.mapping.Document; import org.springframework.data.mongodb…
阅读更多...
Python中Self的详解及使用

Python中Self的详解及使用

大家学Python面向对象的时候&#xff0c;总会遇到一个让人难以理解的存在&#xff1a;self 这个self到底是谁啊&#xff0c;为什么每个类实例方法都有一个参数self&#xff0c;它到底有什么作用呢&#xff1f; 「先下结论&#xff1a;类实例化后&#xff0c;self即代表着实例&…
阅读更多...
[SSM]在WEB中应用MyBtis

[SSM]在WEB中应用MyBtis

目录 MyBatis基础 5.1需求描述 5.2数据库表的设计和准备数据 5.3实现步骤 第一步&#xff1a;引入相关依赖 第二步&#xff1a;引入相关配置文件&#xff0c;放到resources目录下&#xff08;全部放到类的根路径下&#xff09; 第三步&#xff1a;前端页面index.html 第…
阅读更多...
Istio 深入理解数据平面组件 Envoy

Istio 深入理解数据平面组件 Envoy

ingress control承载了控制面和数据面的一个职责&#xff0c;在control里面有一个process&#xff0c;这个进程就承担了反向代理的能力&#xff0c;当有任何请求发过来的时候&#xff0c;会被nginx接收到这个请求并且被转发&#xff0c;基于的规则由ingress control动态配置的&…
阅读更多...
2023年7月1日【青书学堂】考试 计算机应用基础(高起专)

2023年7月1日【青书学堂】考试 计算机应用基础(高起专)

2023年7月1日【青书学堂】考试 计算机应用基础(高起专) 注意：答案仅供参考 成绩：88.8 分 第1题 单选题 在Word的编辑状态,按先后顺序依次打开了d1.doC、d2.doC、d3.doC、d4.doc 4个文档,当前的活动窗口的文档名为____。 A：d1.doc B：d2.doc C：d4.doc D：d3.doc 答案：C 第…
阅读更多...
php代码还原工具，解决goto语句混淆，php goto解密还原

php代码还原工具，解决goto语句混淆，php goto解密还原

在编写php代码时&#xff0c;使用goto语句是一种常见的加密技巧。为了解决goto解码无法阅读这个问题&#xff0c;今天我要向大家介绍一款强大的php goto解密工具。 这款工具的主要功能之一就是php代码的还原。通过对代码进行解析和分析&#xff0c;它能够轻松还原被混淆的goto…
阅读更多...
vim多文件切换快捷键设置

vim多文件切换快捷键设置

1、基本切换指令 vim中在打开多个文件时&#xff0c;会有多个文件进行切换的需求。按:bn切换到下一个文件&#xff0c;按:bp切换到上一个文件。 2、快捷键设置 为了便捷操作&#xff0c;将切换命令设置成快捷键。 进入/home/yys个人目录下&#xff0c;vim .vimrc进入vimrc文…
阅读更多...
Spring Boot 中的 @EnableDiscoveryClient 注解

Spring Boot 中的 @EnableDiscoveryClient 注解

Spring Boot 中的 EnableDiscoveryClient 注解 Spring Boot 是一个快速开发 Spring 应用程序的框架&#xff0c;它提供了一些基础设施&#xff0c;使得我们可以快速地开发出高效、可靠的应用程序。其中&#xff0c;EnableDiscoveryClient 注解是 Spring Boot 中一个非常重要的…
阅读更多...
C++刷题第四天 链表 24. 两两交换链表中的节点 ● 19.删除链表的倒数第N个节点 ● 160. 链表相交 ● 142.环形链表II

C++刷题第四天 链表 24. 两两交换链表中的节点 ● 19.删除链表的倒数第N个节点 ● 160. 链表相交 ● 142.环形链表II

24. 两两交换链表中的节点 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0c;只能进行节点交换&#xff09;。 示例&#xff1a; 原列表为&#xff1a;1-2-3-4-…
阅读更多...
【Mysql】Explain深入分析（三）

【Mysql】Explain深入分析（三）

Explain工具介绍 使用EXPLAIN关键字可以模拟优化器执行SQL语句&#xff0c;分析你的查询语句或是结构的性能瓶颈 在 select 语句之前增加 explain 关键字&#xff0c;MySQL 会在查询上设置一个标记&#xff0c;执行查询会返回执行计划的信息&#xff0c;而不是执行这条SQL 注意…
阅读更多...
node ffmpeg jsmpeg 拉流 展示笔记

node ffmpeg jsmpeg 拉流 展示笔记

拉流参考上一篇 基础&#xff1a;FFmpeg安装过 拉流完成之后转换成可播放的方式 1、下载jsmpeghttps://github.com/phoboslab/jsmpeg 下载完 用vscode 打开jsmpeg-master目录 2、在根目录下安装 node-media-server npm install node-media-server 新建app.js并运行 const…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023