一、仿真实验目的

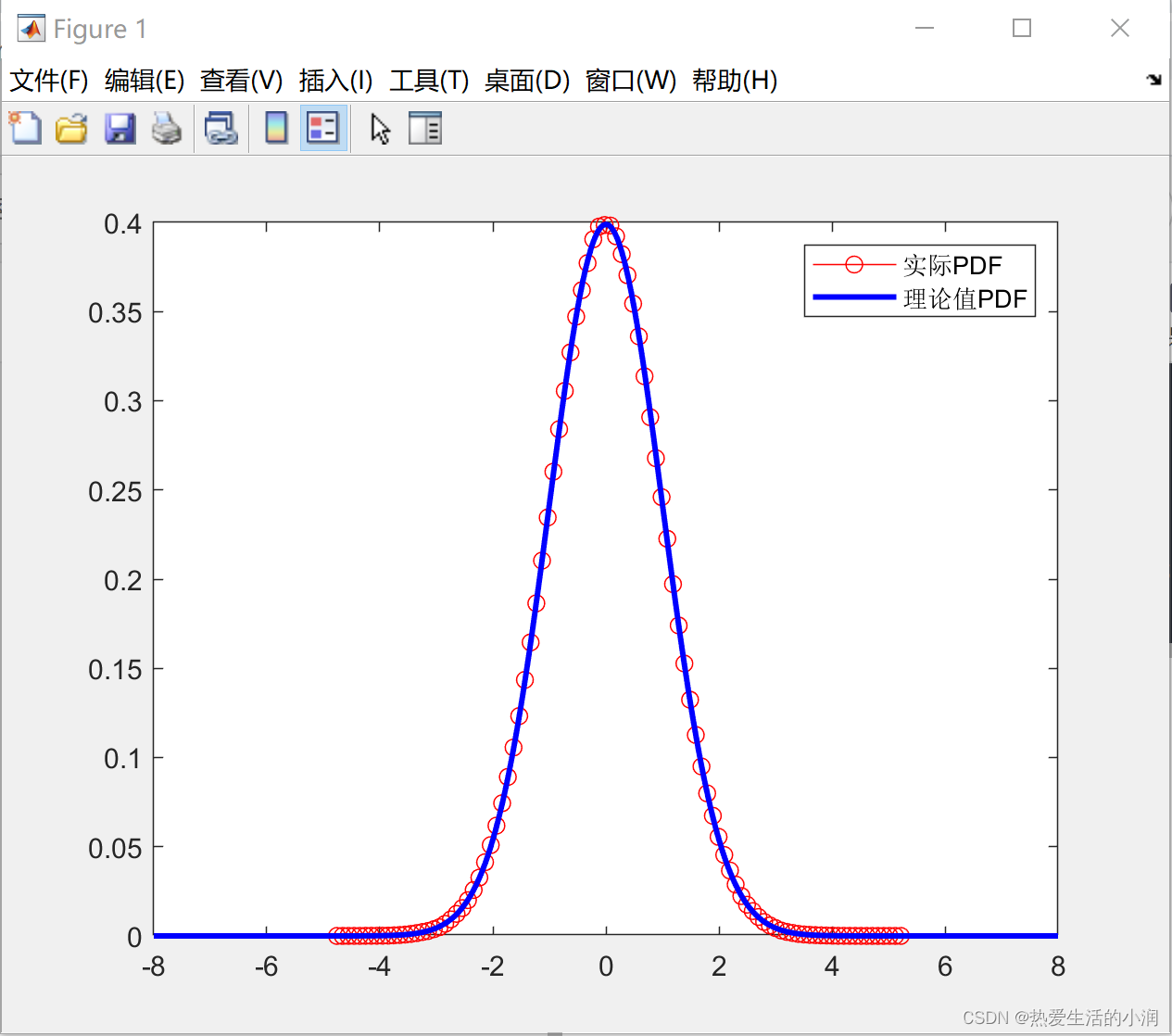
生成一组高斯变量，并基于生成的数据统计其概率密度函数，与理论高斯概率密度函数进行对比，观察生成的高斯变量的概率分布。

二、解决思路

（1）利用randn函数生成高斯随机变量
（2）利用ksdensity由随机变量估计概率密度函数
（3）利用高斯分布的理论公式计算理论概率密度函数
$$f(x)=\frac{1}{\sqrt{2\pi N_0}}\exp \left(-\frac{(x-\mu {)}^2}{2N_0}\right)$$

三、实验代码

clear;close all;clc;

%% 参数设置
Length = 1000000; % 信号长度，用于计算统计的
N0 = 1; % 计算噪声功率
miu = 0; % 均值

x = -8:0.05:8;
n = sqrt(N0)* randn(Length,1); %  1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; % white gaussian noise, 0dB

p = 1 / sqrt( 2*pi*N0 ) .* exp( (-(x-miu).^2)./(2.*N0) ); % 计算理论值，噪声n理论概率密度公式
[pp,xx]=ksdensity(n); % 计算实际值，由随机变量统计概率密度，对于单变量，是估计100个点

%% 作图
figure;
plot(xx,pp,'-ro');
hold on;
plot(x,p,'LineWidth',2,'Color','b');
legend('实际PDF','理论值PDF');

四、实验结果