一：为什么需要离散傅里叶变换

我们知道在傅里叶变换中存在连续信号和离散信号变换从而诞生了有拉普拉斯变换（连续信号）、Z变换（离散信号），这两种变换是方便以前没有计算机时工程师们手动计算傅里叶变换。而随着计算机算力增加，我们希望通过计算机帮助我们计算出傅里叶变换，所以离散傅里叶变换（DFT）（本次讲解）和快速傅里叶变换（FFT）（留在下一篇讲解）就产生了。

二：离散傅里叶变换的思路

思路：想要对一个连续变换的频谱进行抽样

遇到问题：我们所进行采样的工具都是在时域中进行采样，没有进行频域采样的工具。

解决方法：利用时域和频域的性质，如果让时域信号周期化，则频域就变成离散的了。

三：离散傅里叶变换的定义

3.1定义公式

正变换（DFT）和反变换（IDFT）的公式如下图所示：

 公式中：

k为频域中的自变量，X（k）为频域中的序列；

n为时域中的自变量，X（n）为时域中的序列；

N为变换区间的长度（需要注意在DFT中一定要强调是多少长度的DFT，因为不同长度DFT值是有不一样的）；

下面两张图中的红点分别表示取N=4、8的结果图：

 

 

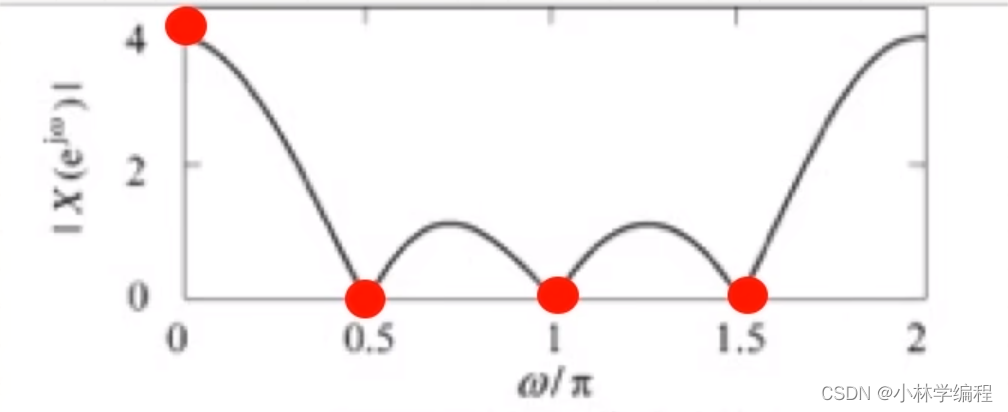
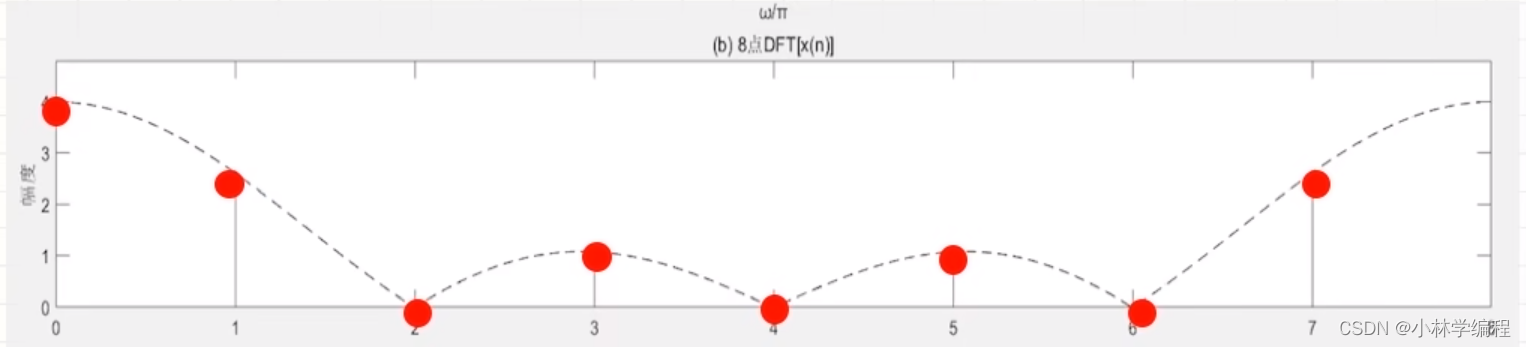
其中；

3.2的理解性计算

我们由3.1中的公式可以知道，那就可以理解成将一个圆平均分成N份并逆时针读数，如下图N=4时的取值：

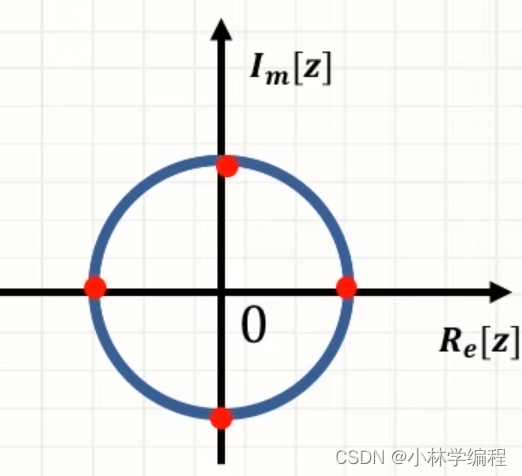
 其中=1；=-j；=-1；=j（之后数字按照周期重复出现）

四：离散傅里叶周期延拓

4.1周期延拓中的符号

如下图符号所示：

其中为周期序列，为以N为周期的周期延拓。

其中x(n)和的关系如下图所示：

 

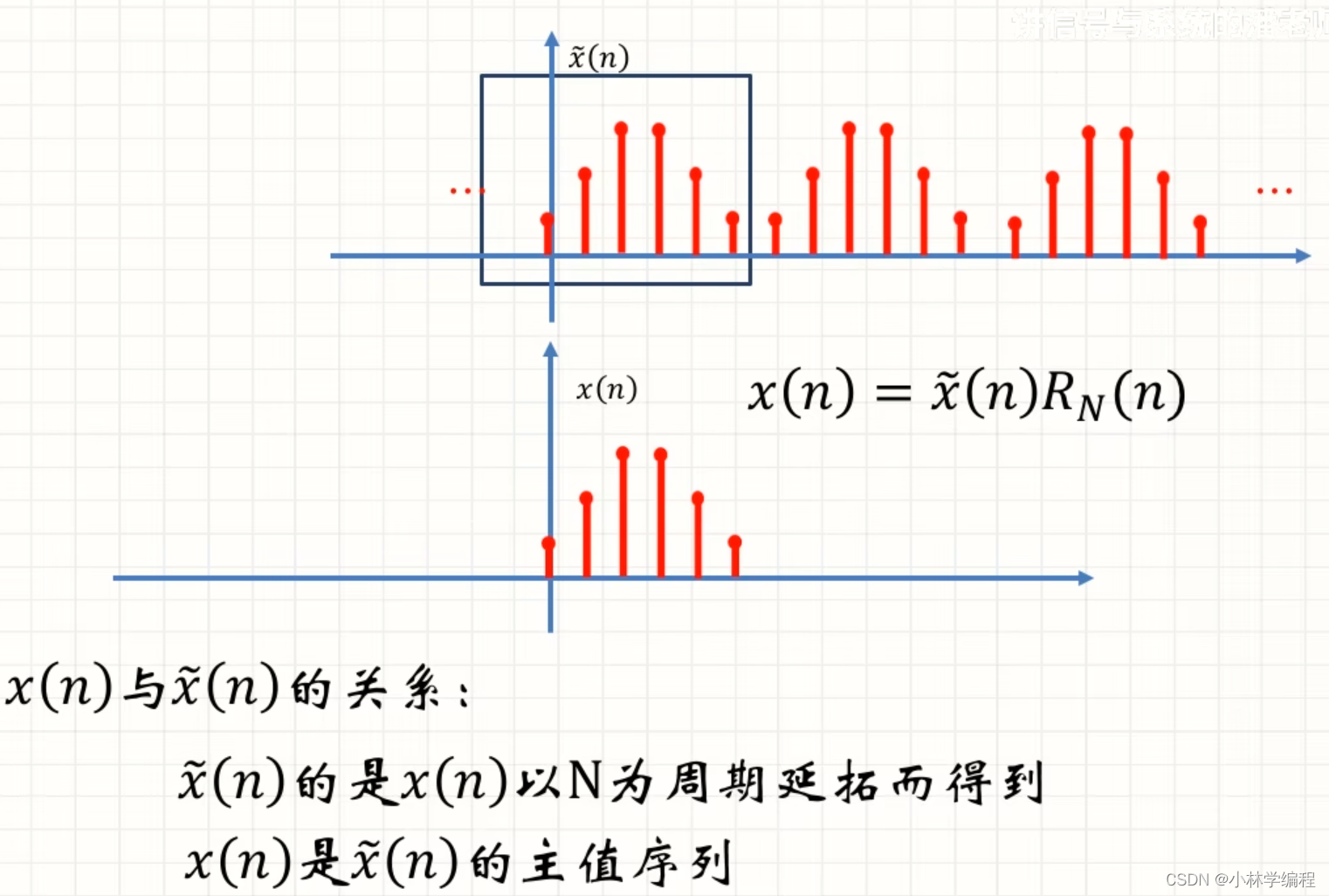
4.2周期延拓的三种情况

周期延拓的关键参数：x(n)序列长度M，周期延拓序列长度N。

（1）当M=N时,直接周期延拓即可，如下图

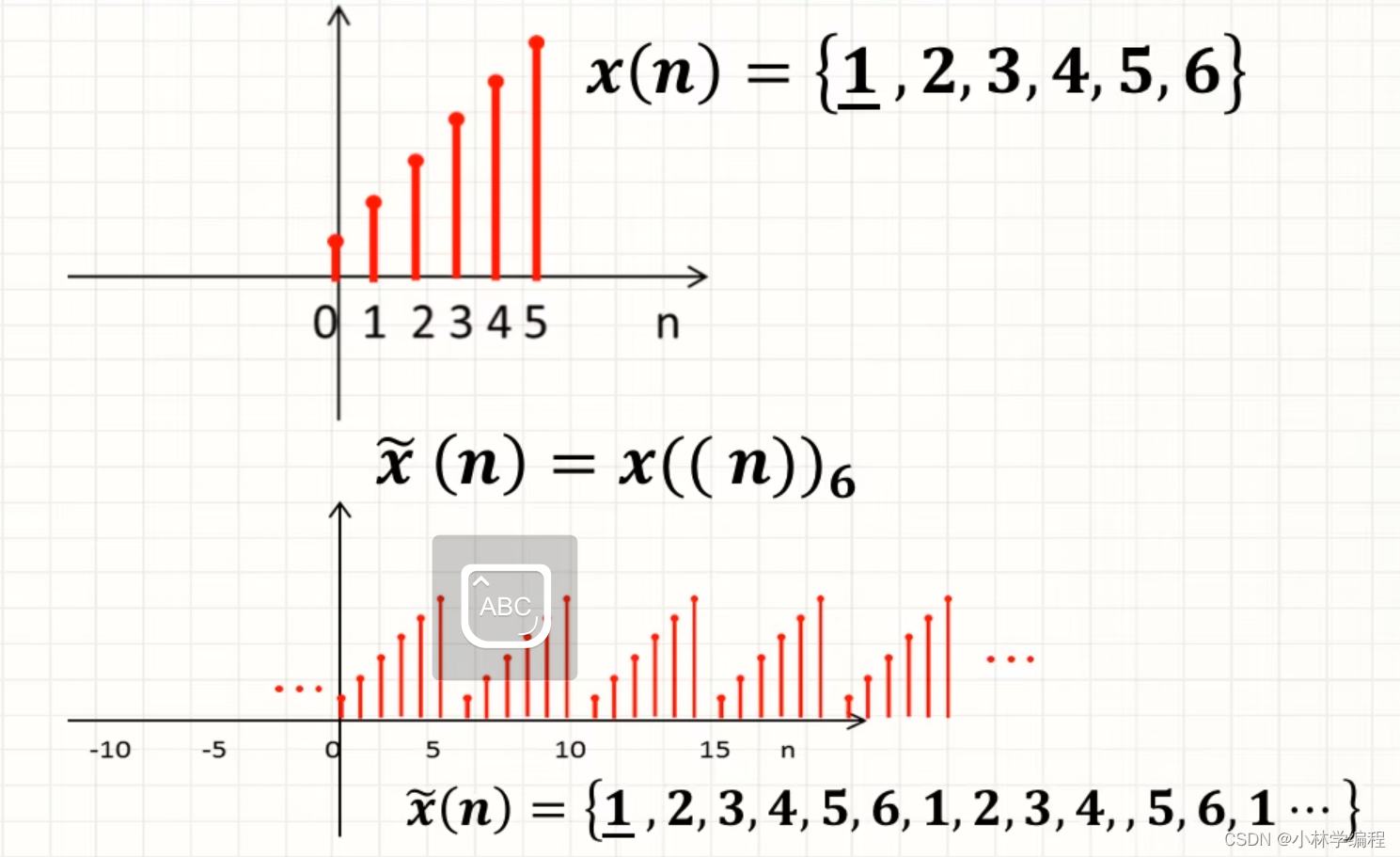
 （2）当M<N时，需要在序列后补齐N-M个零，再进行周期延拓，如下图：

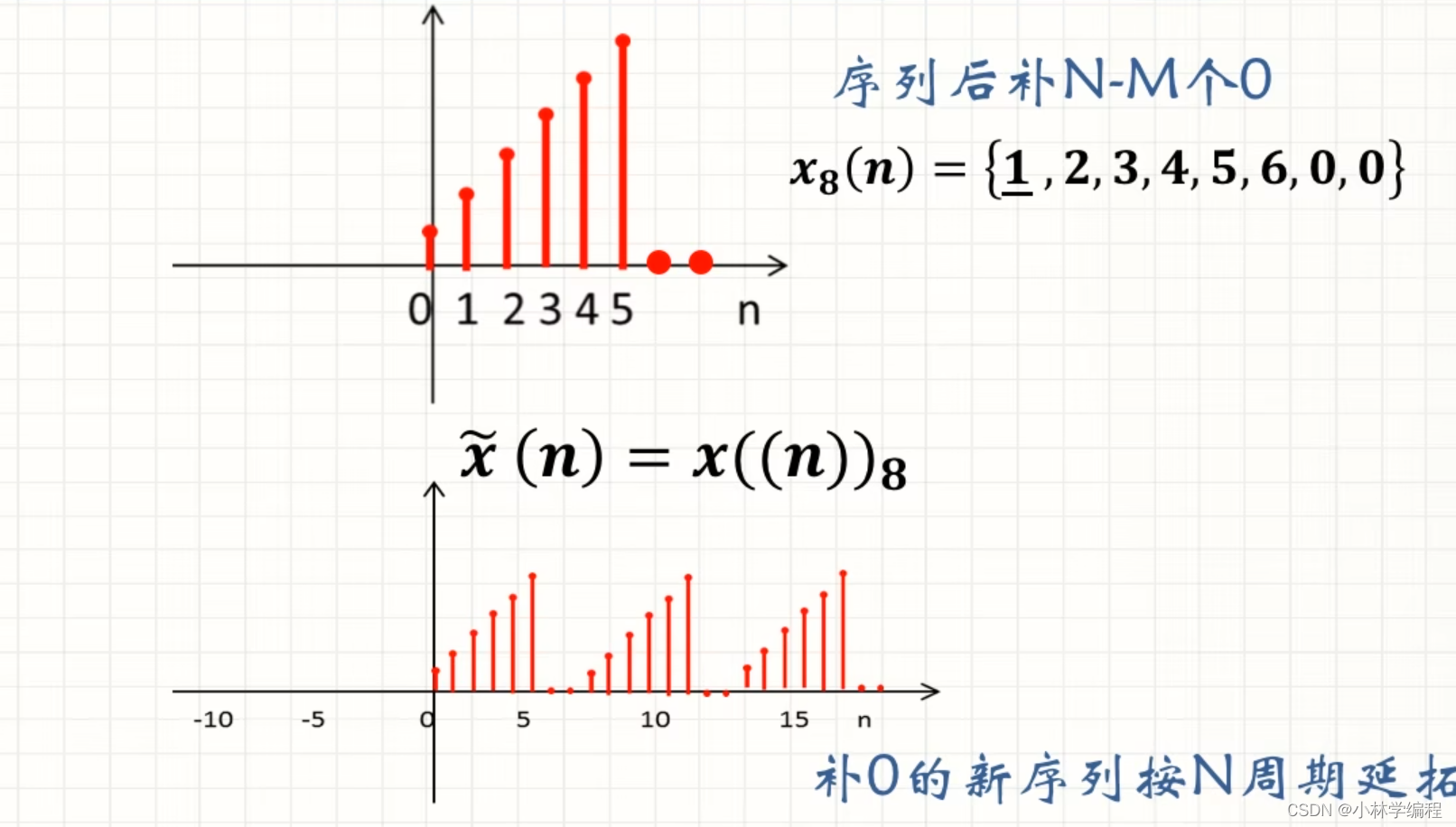
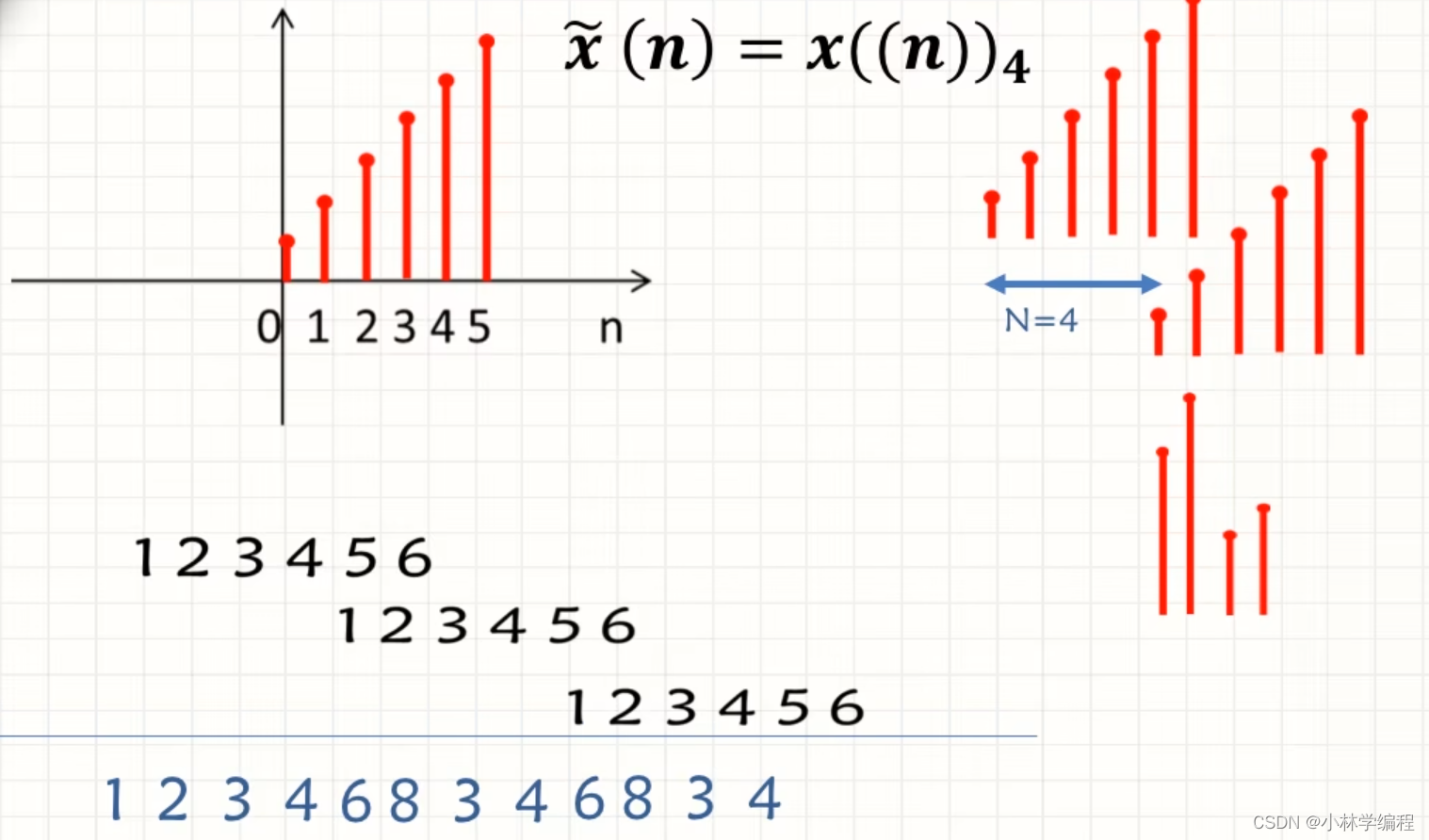
（3）当 M>N时,M=6,N=4时，可以看到以N=4为周期进行延拓的话会有混叠部分，我们把从混叠部分开始的N个数作为周期延拓后的序列，下图周期延拓后的结果为6，8，4，3。

 五：周期序列的傅里叶级数（DFS）

DFT和DFS区别：DFS信号本身就是周期的（自然周期），而不是靠我们上述方法进行周期延拓而来的（而DFT的周期是因为具有周期性，而产生的一种隐含周期，这种周期不是序列自己拥有的那种自然周期，而是通过人为通过序列循环而得到的，所以常常令它的周期与DFT变换周期相匹配）。

因为本身是周期的，不满足绝对可和的傅里叶变换的要求，更谈不上有频域的采样了，所以我们使用傅里叶级数（DFS）来解决。

如下图对比：

 那么就做题而言什么时候使用DFS，那个时候使用DFT呢？如下图解析：

 六：离散傅里叶变换性质

6.1线性

 PS：（1）两个有限长序列的长度可以不一样

（2）但是取变换区间长度时需要取两者长度的最大值，避免混叠的现象。

6.2循环移位性

（1）序列的循环移位：

 

我们用一个例题来直观的看待：

答案如下：

1）先进行补零，然后再周期延拓即可

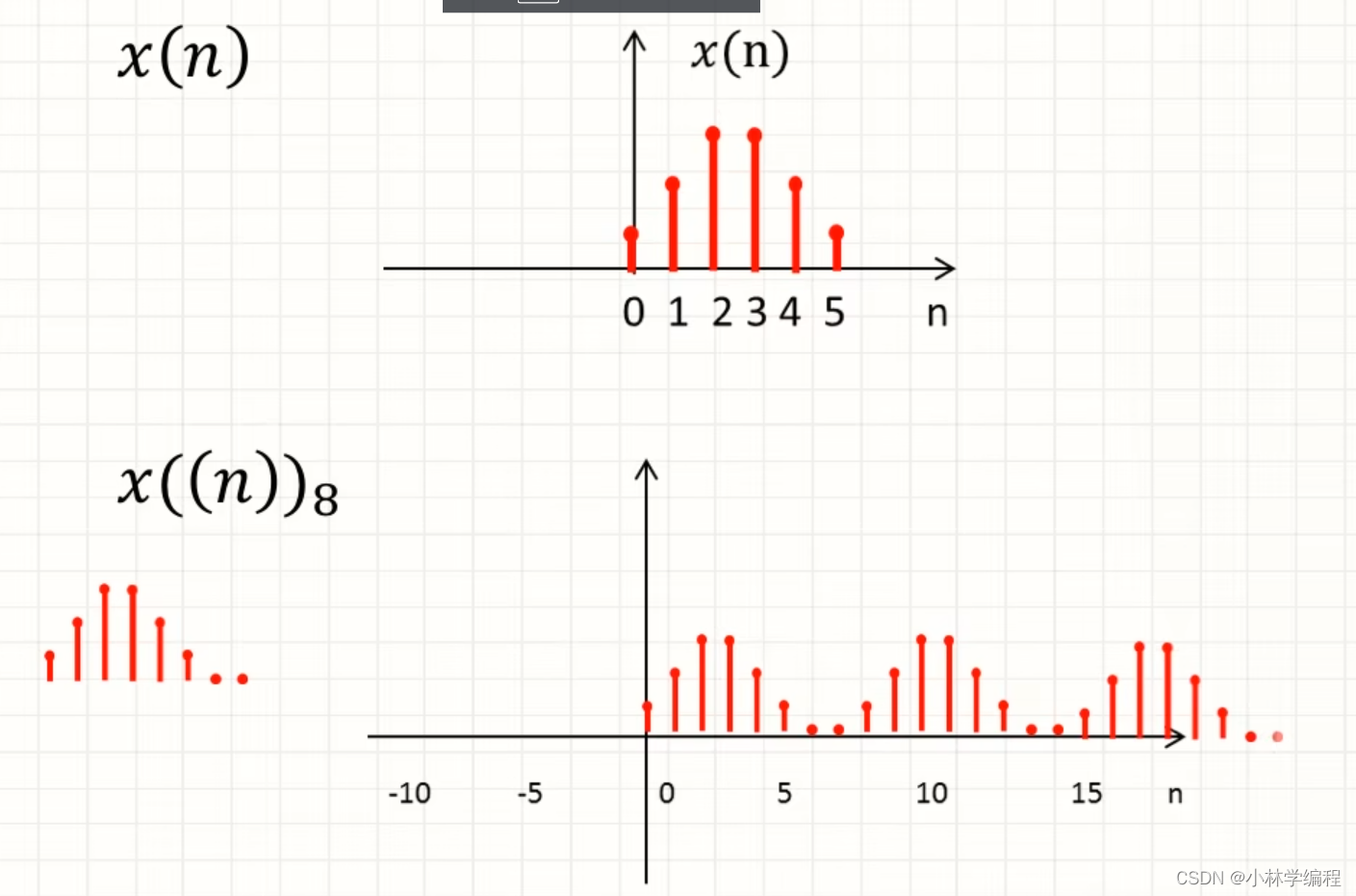
 2）先将X(n)左移两位，再进行周期延拓即可

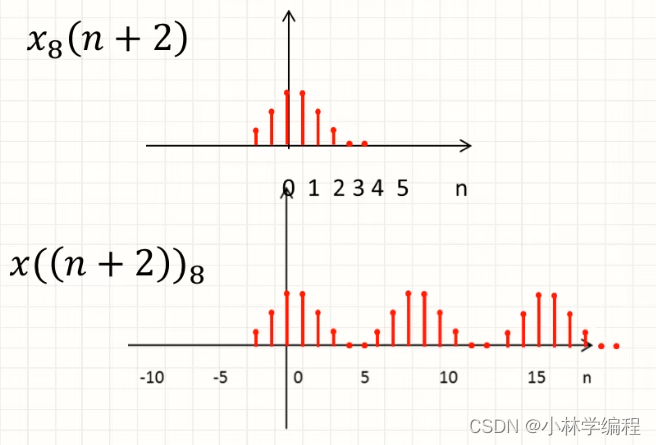
3）对2）中的结果进行从N=0-7取值即可

 

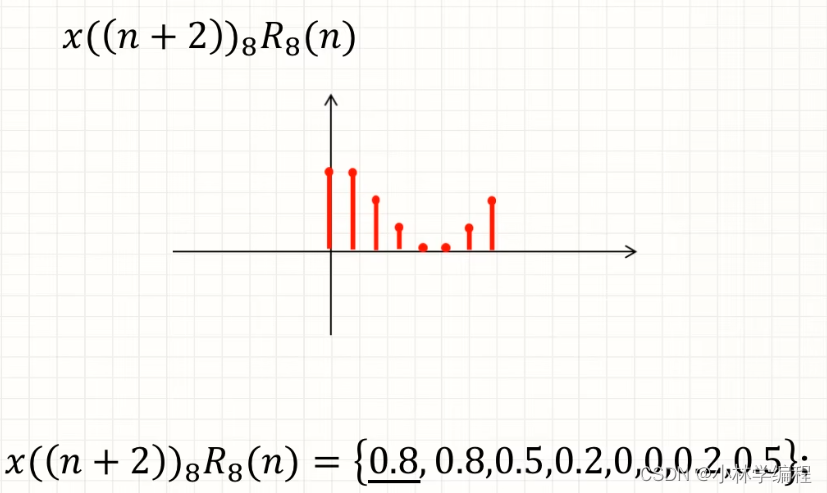
从直觉上来看得到的序列只是进行的将原来序列在N=0,1的值移位到了N=5,6处，所以得名循环移位。

（2）时域循环移位定理

（3）频域循环移位定理 

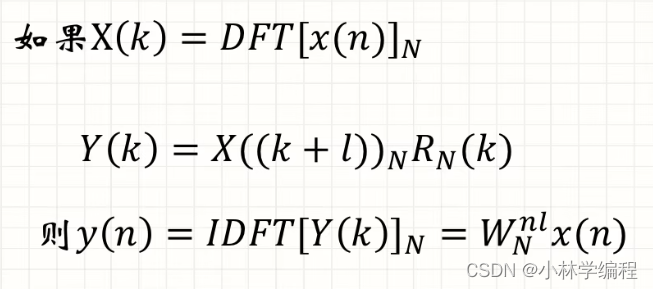
 6.3循环卷积定理

 

给一个例题方便大家理解：

 答案如下：

或者说可以使用简单算法，利用线性卷积和循环卷积的关系求解，具体求解方式，可看最后参考资料的第二点，这里不再赘述。 

6.4 DFT的复共轭性

（1）x(n)的复共轭序列定义

（2）x(n)的复共轭对称特性

 这条性质可以用来减少计算机计算时的时间复杂度（因为可以利用一部分已知的序列求出另一部分未知序列，如知道奇数序列可以得到偶数序列）。

七：频域采样定理

PS：若给出的序列M<N时，先使用周期延拓的方法，先得到x(n)的主值序列，再进行采样即可。 

 八：参考资料

（1）视频P20-P26

3-3频率域采样定理_哔哩哔哩_bilibili

 （2）利用线性卷积和循环卷积的关系求解线性卷积

线性卷积和循环卷积（圆周卷积）_循环卷积和圆周卷积一样吗_叶夏隐的博客-CSDN博客