目录
1. K-Means的工作原理
2.Kmeans损失函数
3.Kmeans优缺点
4.编写KMeans算法实现类
5.KMeans算法测试
6.结果
Kmeans是一种无监督的基于距离的聚类算法,其变种还有Kmeans++。其中,sklearn中KMeans的默认使用的即为KMeans++。使用sklearn相关算法API的调用案例可参考博主另一篇文章:KMeans算法实现图像分割。本文主要通过纯手写的方式,帮助学习理解KMeans算法的数据处理过程。
1. K-Means的工作原理
在K-Means算法中,簇的个数K是一个超参数,需要人为输入来确定。K-Means的核心任务就是根据设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:
- 首先随机选取样本中的K个点作为聚类中心;
- 分别算出样本中其他样本距离这K个聚类中心的距离,并把这些样本分别作为自己最近的那个聚类中心的类别;
- 对上述分类完的样本再进行每个类别求平均值,求解出新的聚类质心;
- 与前一次计算得到的K个聚类质心比较,如果聚类质心发生变化,转过程b,否则转过程e;
- 当质心不发生变化时(当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了),停止并输出聚类结果。
综上,K-Means 的算法步骤能够简单概括为:
1-分配:样本分配到簇。
2-移动:移动聚类中心到簇中样本的平均位置。2.Kmeans损失函数
和其他机器学习算法一样,K-Means 也要评估并且最小化聚类代价,在引入 K-Means 的代价函数之前,先引入如下定义:

引入代价函数:

3.Kmeans优缺点
优点:
1.容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了;
2.处理大数据集的时候,该算法可以保证较好的伸缩性;
3.当簇近似高斯分布的时候,效果非常不错;
4.算法复杂度低。
缺点:
1.K 值需要人为设定,不同 K 值得到的结果不一样;
2.对初始的簇中心敏感,不同选取方式会得到不同结果;
3.对异常值敏感;
4.样本只能归为一类,不适合多分类任务;
5.不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。4.编写KMeans算法实现类
import numpy as np
class KMeans:
def __init__(self, data, num_clusters):
self.data = data
self.num_clusters = num_clusters
def train(self, max_iterations):
centerids = KMeans.centerids_init(self.data, self.num_clusters)
num_examples = self.data.shape[0]
closest_centerids_ids = np.empty((num_examples, 1))
for _ in range(max_iterations):
closest_centerids_ids = KMeans.centerids_find_closest(self.data, centerids)
centerids = KMeans.centerids_compute(self.data, closest_centerids_ids, self.num_clusters)
return centerids, closest_centerids_ids
@staticmethod
def centerids_init(data, num_clusters):
num_examples = data.shape[0]
random_ids = np.random.permutation(num_examples)
centerids = data[random_ids[:num_clusters], :]
return centerids
@staticmethod
def centerids_find_closest(data, centerids):
num_examples = data.shape[0]
num_centerids = centerids.shape[0]
closest_centerids_ids = np.zeros((num_examples, 1))
for example_index in range(num_examples):
distance = np.zeros((num_centerids, 1))
for centerid_index in range(num_centerids):
distance_diff = data[example_index, :] - centerids[centerid_index, :]
distance[centerid_index] = np.sum((distance_diff ** 2))
closest_centerids_ids[example_index] = np.argmin(distance)
return closest_centerids_ids
@staticmethod
def centerids_compute(data, closest_centerids_ids, num_clusters):
num_features = data.shape[1]
centerids = np.zeros((num_clusters, num_features))
for centerid in range(num_clusters):
closest_ids = closest_centerids_ids == centerid
centerids[centerid] = np.mean(data[closest_ids.flatten(), :], axis=0)
return centerids
5.KMeans算法测试
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from cls_kmeans.k_means import KMeans
iris = load_iris()data = pd.DataFrame(data=iris.data, columns=iris.feature_names)
data["species"] = iris.target_names[iris.target]
# print(data.head())
# print(iris.feature_names)
x_axis = iris.feature_names[2]
y_axis = iris.feature_names[3]
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1) # 一行两列,第一个图
for iris_type in iris.target_names:
plt.scatter(data[x_axis][data["species"] == iris_type],
data[y_axis][data["species"] == iris_type],
label=iris_type)
plt.xlabel(x_axis)
plt.ylabel(y_axis)
plt.title("Label Known")
plt.legend()
plt.subplot(1, 2, 2) # 一行两列,第二个图
plt.scatter(data[x_axis][:], data[y_axis][:], label="all_type")
plt.title("Label Unknown")
plt.xlabel(x_axis)
plt.ylabel(y_axis)
plt.show()
# print(np.unique(iris.target).shape[0])
num_examples = data.shape[0]
x_train = data[[x_axis, y_axis]].values.reshape(num_examples, 2)
max_iterations = 50
num_clusters = 3
kmeans = KMeans(data=x_train, num_clusters=num_clusters)
(centerids, closest_centerids_ids) = kmeans.train(max_iterations=max_iterations)
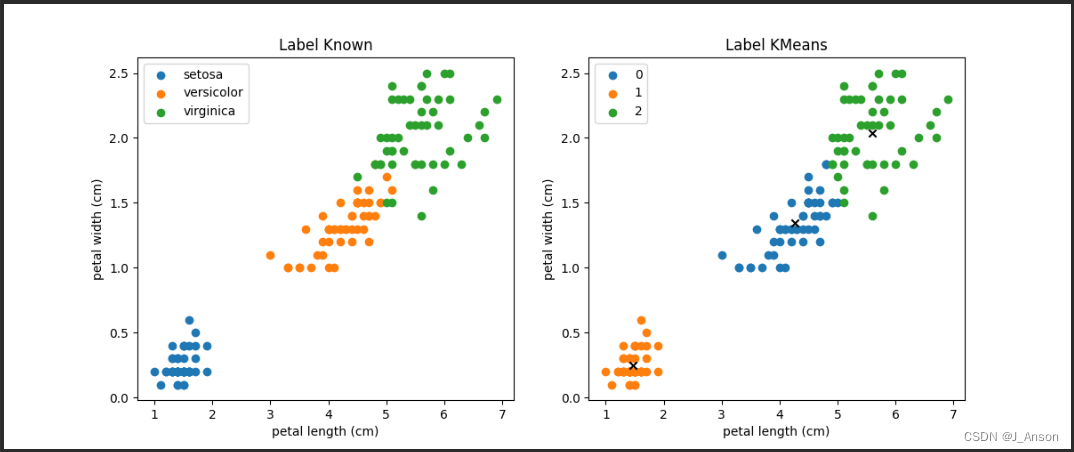
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1) # 一行两列,第一个图
for iris_type in iris.target_names:
plt.scatter(data[x_axis][data["species"] == iris_type],
data[y_axis][data["species"] == iris_type],
label=iris_type)
plt.xlabel(x_axis)
plt.ylabel(y_axis)
plt.title("Label Known")
plt.legend()
plt.subplot(1, 2, 2)
for centerid_id, centerid in enumerate(centerids):
current_example_index = (closest_centerids_ids == centerid_id).flatten()
plt.scatter(data[x_axis][current_example_index],
data[y_axis][current_example_index],
label=centerid_id)
for centerid_id, centerid in enumerate(centerids):
plt.scatter(centerid[0], centerid[1], c="black", marker="x")
plt.xlabel(x_axis)
plt.ylabel(y_axis)
plt.title("Label KMeans")
plt.legend()
plt.show()6.结果